Matricea de transformare este utilizată pentru a calcula coordonatele obiectului nou atunci când este transformată. Schimbând valorile elementelor matricei de transformare, puteți aplica orice transformări obiectelor (de exemplu: scalare, oglindire, rotire, deplasare, etc.). Cu orice transformare, liniile obiectului sunt paralele.
Coordonatele în format PDF sunt exprimate în termeni de spațiu bidimensional. Punctul (x, y) din spațiu poate fi exprimat în forma vectorului [x y 1]. Un al treilea element constant al acestui vector (1) este necesar pentru a utiliza un vector cu matrice 3x3 în calculele descrise mai jos.
Transformarea între cele două sisteme de coordonate este reprezentată ca o matrice 3 × 3 și redactată după cum urmează:
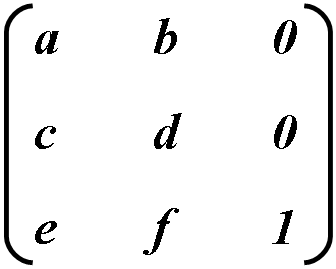
Transformările în coordonate sunt exprimate sub formă de multiplicări de matrice:
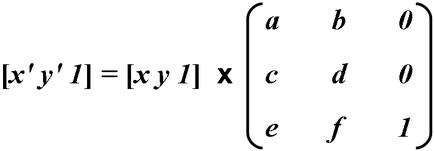
Din moment ce ultima coloană nu are niciun efect asupra rezultatelor calculului, nu participă la calcule. Coordonatele transformării sunt calculate prin următoarele formule:
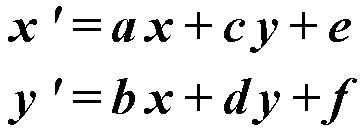
Numita matricea identitate, ca matricea în care și d sunt egale cu 1 și restul 0. Această matrice este utilizată implicit, deoarece aceasta nu duce la transformare. Prin urmare, o bază unică este utilizată ca bază.
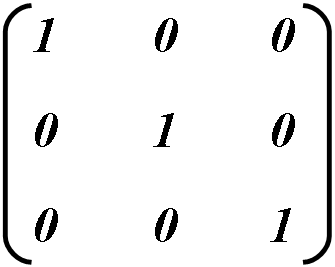
Pentru a mări sau a micșora dimensiunea obiectului orizontal / vertical, schimbați valoarea a sau d și aplicați restul din matricea unității.
De exemplu: Pentru a mări dimensiunea unui obiect de două ori pe orizontală, valoarea a trebuie considerată egală cu 2, iar restul să rămână ca în matricea de identitate.
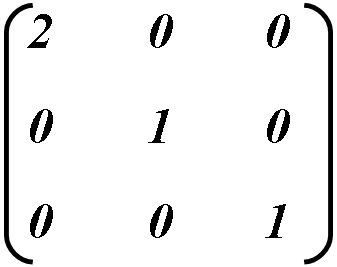
Calculăm noile coordonate ale obiectului:
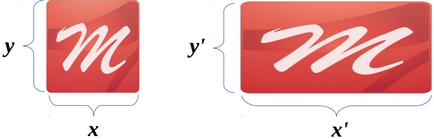
Pentru a obține o imagine în oglindă a obiectului pe orizontală, setați valoarea la a = -1. pe verticală d = -1. Schimbarea ambelor valori este utilizată pentru afișarea simultană a imaginilor orizontale și verticale.
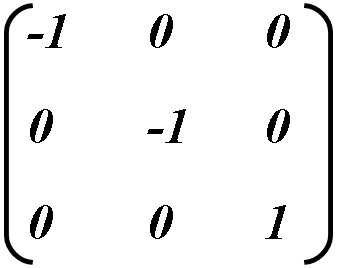
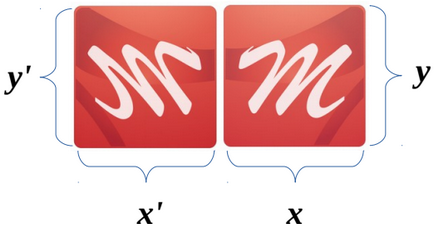
Panta obiectului vertical / orizontal este furnizată prin modificarea valorilor de la b și respectiv c. Schimbați valoarea b / -b - înclinați în sus / în jos, c / -c - dreapta / stânga.
De exemplu: Pentru a înclina obiectul vertical în sus, setați valoarea la b = 1
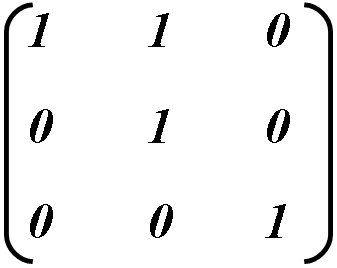
Calculăm noile coordonate ale obiectului:
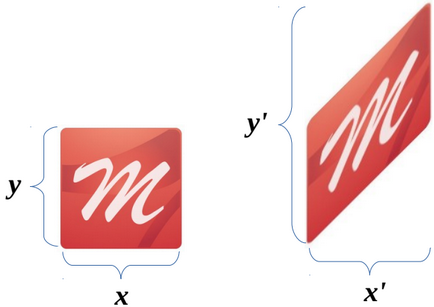
Ca rezultat, numai coordonata y duce la panta obiectului. care crește cu valoarea lui x.
Rotație - o combinație de zoom și de înclinare, dar pentru a păstra proporțiile inițiale ale obiectului, conversia trebuie să fie efectuată cu calcule exacte folosind sinus și cosinus.
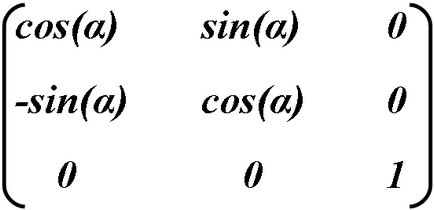
Turnul în sine are loc în sens contrar acelor de ceasornic, α specifică unghiul de rotație în grade.
Mutarea se face prin modificarea valorilor e (orizontal) și f (vertical). Valorile sunt date în pixeli.
De exemplu: Mutare folosind o matrice este rar folosit datorită faptului că această operație se poate realiza prin alte metode, de exemplu, pentru a schimba poziția obiectului în fila Geometrie.
Deoarece matricea de transformare are doar șase elemente care pot fi schimbate, este afișată vizual în PDF [a b c d e f]. O astfel de matrice poate reprezenta orice transformare liniară de la un sistem de coordonate la altul. Matricele transformărilor se formează după cum urmează:
- Mișcările sunt indicate ca [1 0 0 1 tx ty]. unde tx și ty sunt distanțele față de axa sistemului de coordonate orizontal și respectiv vertical.
- Scalarea este indicată ca [sx 0 0 sy 0 0]. Această cântare coordonate, astfel încât 1 unitate în dimensiunile orizontale și verticale în noul sistem de coordonate de aceeași mărime ca și unități sx și sy în vechiul sistem de coordonate respectiv.
- Rotațiile sunt produse de matrice [cosθ sinθ-sinθ cosθ 0 0]. care corespunde rotației axelor sistemului de coordonate cu grade înclinate în sens contrar acelor de ceasornic.
- Panta este indicată ca [1 taná tanβ 1 0 0]. care corespunde înclinației axei x de unghiul α și axa y de unghiul β.
Figura de mai jos prezintă exemple de transformare. Direcțiile de deplasare, unghiul de rotație și înclinare, prezentate în figură, corespund valorilor pozitive ale elementelor matricei.
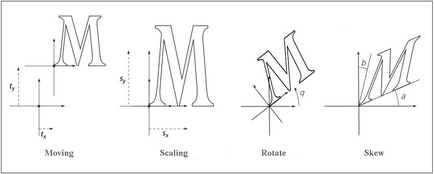
Înmulțirea matricilor nu este comutativă - ordinea în care sunt multiplicate matricele are o valoare.
Tabelul de mai jos prezintă conversiile admise și valorile matricei.