3.2 Informații generale despre inductoare
Bobina de inductanță este un conductor izolat înfășurat în spirală având o inductanță semnificativă, cu o capacitate relativ mică și o rezistență activă mică.
Inductor constă dintr-un singur nucleu, rareori irecuperabile, sârmă izolat înfășurat în jurul cadrului unui dielectric toroidal formă cilindrică sau dreptunghiulară, în conformitate cu figura 3.1, există, de asemenea, inductor frameless.
Winding-ul este un strat (obișnuit și cu pas) și multi-strat (obișnuit, vnaval, universal).
Pentru a crește inductivitatea, se folosesc nuclee de materiale feromagnetice: oțel electric, permalloy, fier carbonil, ferite. Miezurile sunt de asemenea folosite pentru a schimba inductanța circuitelor rezonante în limite mici.
Valoarea inductanței inductorului este proporțională cu dimensiunile liniare ale bobinei, pătratul numărului de rotații de înfășurare și permeabilitatea magnetică a miezului și variază de la zeci de pg la zeci de grame.
Parametrii principali ai inductorului sunt rezistența la pierderi, factorul de calitate, coeficientul termic al inductanței, capacitatea proprie.
Inductorii sunt utilizați pe scară largă ca elemente ale filtrelor și circuitelor oscilatorii, în transformatoare, cum ar fi comutatoare, relee, amplificatoare magnetice, electromagneți etc.
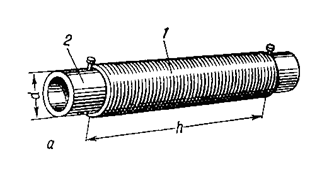
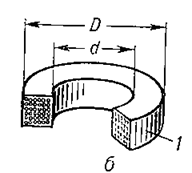
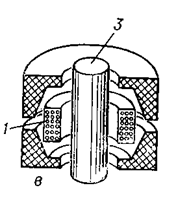
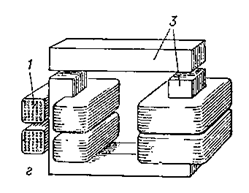
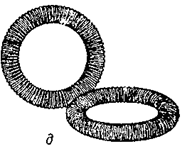
Figura 3.1 - Bobine de inductanță:
a) un singur strat cilindric;
b) multistrat toroidal;
c) cu un miez cilindric;
d) cu un miez în formă de U;
e) inductanța de referință pe un toroid ceramic;
1 - înfășurare (sârmă);
h este lungimea înfășurării;
d este diametrul interior al înfășurării;
D este diametrul exterior al înfășurării.
Un solenoid este o bobină de inductanță realizată sub forma unui conductor izolat înfășurat în jurul unui cadru cilindric, de-a lungul căruia curge un curent electric. Solenoidul este un sistem de curenți circulari de aceeași rază, având o axă comună în conformitate cu Figura 3.2-a.
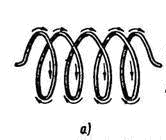
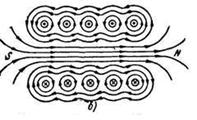
Figura 3.2 - Solenoidul și câmpul său magnetic
În cazul în care se taie mental peste bobinele solenoid, indică direcția curentului în ele, așa cum sa menționat mai sus, și de a determina direcția liniilor de inducție magnetică de „regula dreapta“, câmpul magnetic în toate solenoid va avea aspectul așa cum se arată în figura 3.2-b.
Pe axa unui solenoid infinit de lung, pe fiecare unitate din care se înfășoară n0 ture, intensitatea câmpului este determinată de formula:
În locul unde liniile magnetice intră în solenoid, se formează polul sudic, unde ieșesc - polul nordic.
Pentru a determina polii electrovalve sunt „regula dreapta“, aplicarea acesteia după cum urmează: în cazul în care un sfredel poziționat de-a lungul axei electrovalve și rotiți-l pe direcția curentului în spirele bobinei electromagnetice, mișcarea de translație a degetului mare va indica direcția câmpului magnetic, în conformitate cu figura 3.3.

Figura 3.3 - Aplicarea regulii de perforare
Solenoidul, în interiorul căruia este amplasat miezul de oțel (fier) conform figurii 3.4, se numește electromagnet. Câmpul magnetic al unui electromagnet este mai puternic decât cel al unui solenoid, deoarece o bucată de oțel încorporată într-un solenoid este magnetizată și câmpul magnetic rezultat este amplificat.
Stâlpii unui electromagnet pot fi determinați, precum și un solenoid, în conformitate cu "regula călăului".
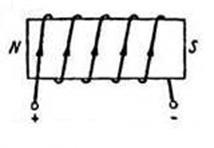
Figura 3.4 - Polii solenoizi
Fluxul magnetic al solenoidului (electromagnet) crește cu numărul de viraje și curentul din el. Forța de magnetizare depinde de produsul curentului pe numărul de viraje (numărul de amperi).
Dacă, de exemplu, luăm un solenoid cu un curent de 5 A de-a lungul înfășurării și numărul de viraje este egal cu 150, atunci numărul de virajuri de amperi va fi 5 • 150 = 750. Același flux magnetic va fi obținut dacă vom lua 1500 de rotații și vom trece printr-un curent de 0,5A, deoarece 0,5 • 1500 = 750 amperi.
Creșteți fluxul magnetic al solenoidului în următoarele moduri:
a) introduceți un miez de oțel în solenoid, transformându-l într-un electromagnet;
b) creșterea secțiunii transversale a miezului de oțel al electromagnetului (deoarece la creșterea curentului, intensitatea câmpului magnetic și deci a inducției magnetice, o creștere a secțiunii transversale conduce la o creștere a fluxului magnetic);
c) reduceți spațiul de aer al electromagnetului (deoarece rezistența magnetică scade odată cu scăderea traiectoriei magnetice prin aer).
Inducția solenoidului. Inductanța solenoidului se exprimă după cum urmează:
unde V este volumul solenoidului.
Fără utilizarea materialului magnetic magnetic inducției magnetice B în interiorul bobinei este, de fapt, constant și este egală cu
B = # 956; 0Ni / l (3,9)
unde # Permeabilitatea magnetică a vidului;
N este numărul de viraje;
l este lungimea bobinei.
Neglijând efectele de margine la capetele solenoidului, obținem că legătura fluxului prin bobină este egală cu densitatea de flux B înmulțită cu suprafața secțiunii transversale S și cu numărul de curbe N:
Din această formulă pentru bobina inductanță este echivalentă cu cele două formule anterioare
Solenoid pe curent continuu. Dacă se utilizează o lungime solenoid mult mai mare decât diametrul său și material magnetic, atunci când un curent trece prin bobina în interiorul bobinei creează un câmp magnetic direcționat de-a lungul unei axe care este omogenă și constantă de curent egală în mărime
unde # Permeabilitatea magnetică a vidului;
n = N / l este numărul de rotații pe unitate de lungime;
I - curent în lichidare.
Când curentul curge, solenoidul stochează energia egală cu munca care trebuie făcută pentru a stabili curentul curent I. Valoarea acestei energii este
Când se schimbă curentul în solenoid, apare un EMF de auto-inducție, valoarea căreia
Solenoid cu curent alternativ. Cu curent alternativ, solenoidul creează un câmp magnetic alternativ. Dacă solenoidul este folosit ca electromagnet, atunci cantitatea de forță de atracție variază cu curent alternativ. În cazul unei armături dintr-un material magnetic moale, direcția forței de atracție nu se modifică.
În cazul unei ancore magnetice, direcția forței se modifică. În curent alternativ, solenoidul are o rezistență complexă, componenta activă a căreia este determinată de rezistența activă a înfășurării, iar componenta reactivă este determinată de inductanța înfășurării.
Aplicarea solenoidelor. Solenoizii DC sunt utilizați cel mai adesea ca servomotor de putere progresivă. Spre deosebire de electromagneții convenționali, acesta oferă un accident vascular cerebral mare. Caracteristica de putere depinde de structura sistemului magnetic (miez și carcasă) și poate fi aproape de liniar. Solenoide fixate în foarfece de mișcare pentru tăierea biletelor și cecuri în case de marcat, încuietori de încuietori, supape în motoare, sisteme hidraulice și așa mai departe.
Solenoizii AC sunt utilizați ca inductor pentru încălzirea prin inducție în creuzete de inducție.
4. Calculul dispozitivului de magnetizare pentru metoda particulelor magnetice de testare nedistructivă
Intrare pentru calcul:
1 Solenoid de secțiune rotundă cu diametrul de 30 mm și lungimea de 200 mm;
2 Material de bază - Oțel 20;
3 Sârmă a bobinei solenoidului este cupru;
4 Rezistența câmpului magnetic în centrul solenoidului este de 100 A / cm la un curent constant de 1A.
Inducția magnetică a câmpului B este legată de rezistența câmpului magnetic H prin relația pentru aer; prin urmare, formula este reprezentată în forma
Dacă bobinele solenoidului sunt situate îndeaproape sau foarte aproape unul de altul, atunci solenoidul poate fi considerat ca un sistem de curenți circulari conectați succesiv, de aceeași rază, cu o axă comună.
Luați în considerare câmpul de întoarcere circulară cu curent. Centrul O cu raza R a unei bobine circulare cu un curent electric I vectori dB câmpuri magnetice ale elementelor bobinelor mici în aceeași direcție - perpendiculară pe planul bobinei (pentru desen), conform figurii 4.1.
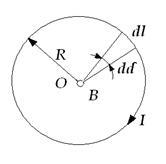
Figura 4.1 - Inducția magnetică a unei viraje circulare cu un curent
Vectorul B al câmpului rezultat al întregii revoluții este, de asemenea, direcționat. Prin legea Bio-Savar-Laplace:
unde este unghiul la care este observat elementul dl al virajului de la ochelarii O.
Integrarea acestei expresii peste toate elementele revoluției, adică pe l de la 0 la 2πR sau prin # 945; de la 0 la 2π, obținem:
Să determinăm acum inducția magnetică a câmpului de întoarcere cu curentul într-un punct situat pe axul rândului; pe linia dreaptă OO 'care trece prin centrul rândului perpendicular pe planul său, în conformitate cu figura 4.2.
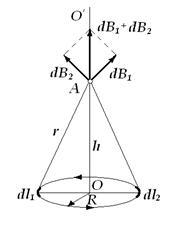
Figura 4.2 - Inducția magnetică a câmpului de întoarcere cu un curent la un punct arbitrar
Figura arată o întoarcere circulară a razei R, a cărei plan este perpendicular pe planul desenului, iar axa OO 'se află în acest plan. La punctul A pe axa OO "vectorii pentru câmpurile diferitelor elemente mici dl de la rândul său cu curent nu coincid în direcție. Vectorii dB1 și dB2 pentru câmpurile a două elemente diametral opuse ale rândului dl1 și dl2. având aceeași lungime (dl1 = dl2 = dl), sunt egale în valoare absolută:
Vectorul dB1 + dB2 rezultat este direcționat la punctul A de-a lungul axei OO 'a rândului, și
Vectorul B de inducție la punctul A pentru câmpul magnetic al întregii bobine este de asemenea orientat de-a lungul axei OD, iar modulul său
Dacă vom folosi conceptul vectorului pm al momentului magnetic al bobinei cu curentul I
unde S este aria suprafeței delimitată de contur,
atunci expresia (4.6) poate fi rescrisă în formă
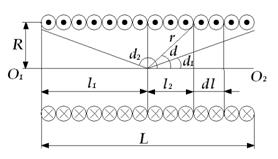
Figura 4.3 - Secțiunea solenoidului
Figura 4.3 prezintă secțiunea transversală a unui solenoid cu raza R și lungimea L cu curentul I. Fie n numărul de ture pe unitatea de lungime a solenoidului.
Inducția magnetică B a câmpului solenoid este egală cu suma geometrică a inducțiilor magnetice Bi a câmpurilor tuturor vârfurilor acestui solenoid. La punctul A, situată pe axa solenoidului O1O2. toți vectorii Bi și vectorul rezultat B sunt direcționați de-a lungul axei O10 în direcția în care gaura dreaptă se mișcă atunci când mânerul se rotește în direcția curentului electric în bobinele solenoidului. O secțiune mică a unui solenoid cu lungimea dl de-a lungul axei are o rotație ndl. Dacă l este distanța de la aceste ture la punctul A, atunci conform formulei (4.8), inducția magnetică a câmpului acestor ture
În cazul nostru, prin urmare
Luând în considerare formula (4.1), echivalăm valorile inducției magnetice și obținem o expresie pentru intensitatea câmpului magnetic:
Din această formulă găsim numărul de rotații de înfășurare pe unitatea de lungime a solenoidului:
Înlocuind valorile cunoscute în formula (4.14), obținem n = 102 în 1 cm.
Numărul de rotații de lichidare se găsește după formula:
Obținem N = 2040 de rotații.
Pentru a înfășura solenoidul în conformitate cu curentul care trece prin el, selectăm firul de cupru conform tabelului 4.1.
Tabelul 4.1 - Parametrii de bază ai firelor de înfășurare a cuprului
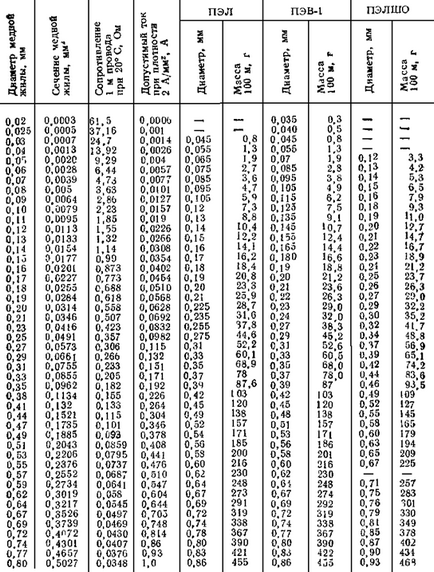
Astfel, alegem un fir de marcă PEV-1 cu un diametru de secțiune de 0,86 mm.
Numărul de rotații ale unui fir dintr-o secțiune transversală dată care se încadrează în lungimea unui solenoid este determinat de formula:
Înlocuind datele cunoscute, obținem N = 233 de rotații. Aceasta este, în cazul nostru, o bobină nouă-strat este obținut.
Calculam masa solenoidului. Pentru a face acest lucru, calculăm mai întâi masa lichidării sale. Pentru a face acest lucru, trebuie să calculam lungimea firului de înfășurare. Acesta poate fi calculat prin cunoașterea numărului de viraje și a lungimii fiecărui rând. Dat fiind faptul că raza înfășurării în fiecare strat de înfășurare se va schimba în conformitate cu figura 4.4, se calculează separat lungimea firului de înfășurare al fiecărui strat.
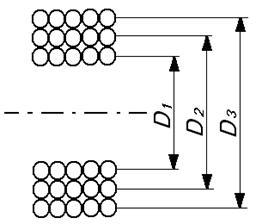
Figura 4.4 - Secțiunea solenoidului
Pentru primul strat al înfășurării, raza înfășurării va fi egală cu suma diametrului solenoidului și a celor două raze ale firului.
Obținem D1 = 30,86 mm.
Lungimea curbelor de înfășurare se calculează prin formula
Lungimea înfășurării bobinei primului strat este C1 = 96,9 mm.
Lungimea înfășurării primului strat se calculează ca fiind rezultatul numărului de rotații și lungimii unei singure rotații:
Obținem l1 = 22,6 m.
Efectuând astfel de calcule, obținem lungimile tuturor înfășurărilor de înfășurare: