DEFINIȚIE O similitudine cu un coeficient este transformarea planului sub care se înmulțesc toate distanțele.
1. Orice mișcare este o similitudine cu un coeficient.
2. O homothety cu un centrometru și coeficient este o cartografiere a planului în sine, sub care un punct este pus în corespondență cu fiecare punct astfel încât.
Verificați dacă homotetul este o mapare bijectivă și, prin urmare, este o transformare plană.
Pentru orice două puncte și imaginile lor sub homothety, avem. Apoi și. adică, homotetul cu un coeficient este o similitudine cu un coeficient.
Din condiție obținem formulele homothety
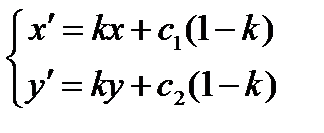
Să dovedim proprietățile omotetei:
a. Sub homothety, o linie dreaptă care nu trece prin centrul homothety trece într-o linie paralelă cu ea, și o linie dreaptă care trece prin centrul homothety se transformă în ea însăși.
b. Homothety păstrează relația simplă a trei puncte de linie dreaptă, ceea ce înseamnă că menține relația "se află între", iar segmentul se traduce într-un segment, o rază într-o rază, un unghi în unghi.
c. Homothety traduce unghiul într-un unghi egal (De ce?).
d. Homotetul păstrează orientarea planului. Pentru a demonstra această proprietate, găsim, prin formulele de homothety, coordonatele punctelor care definesc cadrul de referință al cadrului sub homothety. Apoi găsim coordonatele vectorilor de referință ai cadrului și vedem că determinantul matricei tranziției de la baza cadrului la baza cadrului este egal cu. adică, cadrele și sunt orientate în mod egal.
Teorema Teorema 1. (descompunerea similaritate în compoziție și mișcare homothetic) Orice transformare similaritate poate fi reprezentat ca un homothety cu același raport compoziție și mișcarea.
Dovada lemnei. Să fie o similitudine cu un coeficient. Dacă este o homothety cu coeficient. atunci este o homothety cu coeficient. Apoi compoziția este o mișcare și avem o reprezentare a asemănării sub forma unei compoziții de homothety cu același coeficient și mișcare.
Din această teoremă și din proprietățile omotetei și mișcării, obținem proprietățile asemănărilor:
- Similaritatea are o linie dreaptă la o linie dreaptă.
- Similitudinea păstrează raport simplu de trei puncte pe linie, și salvează astfel relația „între minciună“ și segmentul traduce fascicul de segment de linie din unghiul fasciculului de colț în semiplanul semiplanul.
- Similaritatea traduce unghiul într-un unghi egal.
- Există asemănări de tip I și II.
- Setul P al tuturor similitudinilor planului este un grup cu privire la compoziția transformărilor. Subgrupurile acestui grup sunt: grupul tuturor mișcărilor avionului, setul de toate homotheties cu un centru comun, setul de toate homotheties și traduceri paralele.
- Figurile sunt numite similare. dacă sunt echivalente cu grupul de similaritate P. Exemple de astfel de figuri sunt două triunghiuri ale căror laturi sunt proporționale, două elipse (două hiperbola) ale căror excentricități sunt egale, oricare două parabole.