4.1 Un număr complex este o expresie a formei:
unde u sunt numere reale și a este așa-numita unitate imaginară care satisface condiția
Numerele u sunt numite, respectiv, părțile reale și imaginare ale numărului complex.
Numerele complexe pot fi reprezentate de punctele unui plan sau de vectorii acestui plan.
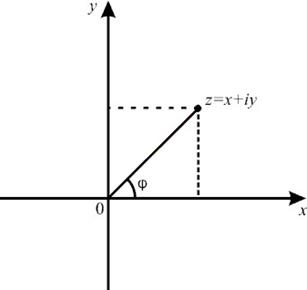
4. 2. Lungimea unui vector se numește modulul unui număr complex și este notat cu. așa că.
Unghi. formată de un vector cu direcția pozitivă a axei se numește argumentul unui număr complex și este notat cu
unde este valoarea principală. determinate de condițiile respective. și,
Deci, cum. . atunci este o formă trigonometrică a unui număr complex. Folosind formula lui Euler
se poate trece de la forma trigonometrică la cea exponențială
4. 3. Două numere complexe și sunt egale dacă și numai dacă părțile lor reale și imaginare sunt egale :; . Sau când modulele lor sunt egale, iar argumentele sunt egale sau diferă printr-un multiplu de:
4. 4. Acțiuni de bază ale numerelor complexe.
La adăugarea și scăderea numerelor complexe, părțile lor reale și imaginare sunt adăugate sau scoase separat
Expansiunea în întregime):
Rădăcina numărului complex este întreg):
Rădăcina oricărui grad din orice număr are valori diferite, care se află la vârfurile obișnuite - un gon inscripționat într-un cerc de rază cu centrul de la origine.
Un exemplu. Numere complexe sunt date în formă algebrică:
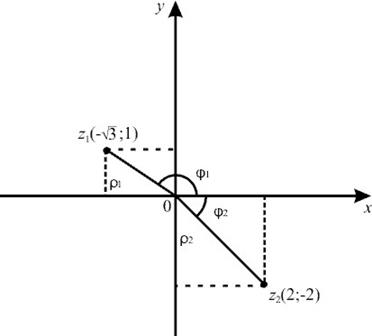
Efectuați următoarele acțiuni :. . . . Găsiți toate rădăcinile ecuației. să le reprezinte într-un avion.
Reprezentăm numerele în planul complex
Forma indicativă a numărului :; .
Înmulțim în funcție de regulile de multiplicare pentru polinoame, luând în considerare și acest lucru. (Atunci când se înmulțește, numărul crește).
În forma demonstrativă:
. (Atunci când se împarte, cifrele sunt scăzute).
4). Este mai bine să realizați această acțiune în formă exponențială
Să găsim rădăcinile ecuației. .
Rădăcina gradului al treilea al unui număr complex are trei semnificații diferite. În acest caz
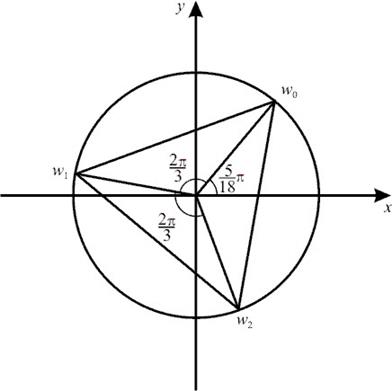
au același modul, astfel încât acestea sunt situate pe un cerc cu centrul la originea coordonatelor, rază. deoarece diferența dintre argumente. apoi se află la vârfurile unui triunghi inscripționat regulat.