1. Metoda de determinare a limitelor folosind tangenta la curba A, B si C
Considerăm metoda de separare a unui set de obiecte de control, ordonate prin coborârea semnului importanței obiectului, cu ajutorul unei tangente la curba analizei ABC [31]. Curba ABC este construită într-un sistem de coordonate dreptunghiular. Pe axa OX, obiectele de gestionare (de exemplu, elementele de sortare) sunt reprezentate în ordinea descrescătoare a procentului din rezultatul total (de exemplu, procentul din implementare), în procente față de numărul total de obiecte de administrare. Pe axa OY, ponderea contribuției obiectului (ponderea vânzărilor pe poziții) este amânată în rezultatul global (în implementarea totală), calculat pe baza totalului cumulat și exprimat în procente (Figura 31).
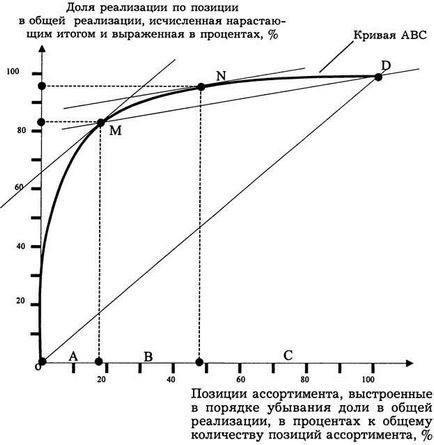
Fig. 31. Separarea setului investigat în grupuri A. B și C prin intermediul unei tangente la curba ABC
Conectăm începutul și sfârșitul graficului liniei drepte OD și apoi tragem o tangență la curba ABC. paralel cu linia OD. Abscisa punctului de tangență (punctul M) ne va arăta limita dintre grupurile A și B. Și ordinul va indica contribuția grupului A la rezultatul total.
Acum, conectăm punctul M cu capătul curbei - punctul D și tragem o nouă tangență la graficul ABC. paralel cu linia MD. Abscisa punctului de tangență (punctul N) indică limita dintre grupurile B și C. iar ordonata arată contribuția totală a grupurilor A și B la rezultatul general.
2. Metoda de determinare a limitelor utilizând buclă de analiză ABC [32]
Soluția propusă definește ca limite ale seturilor A. B și C zonele de schimbare a curburii ascuțite ale graficului ABC.
În Fig. 30 prezintă o formă tipică a curbei ABC. Imaginați-vă că această curbă este harta de parcurs, de-a lungul căreia o mașină de curse se deplasează de-a lungul fundului (de la punctul 0) în direcția rândului, fără a reduce maximul posibil pe un drum drept. Locul unde este aruncat din drum, caracterizat printr-o creștere accentuată a curburii graficului. În acest moment, regiunea de creștere accentuată a valorii caracteristicilor (grupa A) este înlocuită de regiunea de creștere netedă (grupa B).
Direcționarea mental masina la viteza maxima în direcția opusă (în fig. 30 la sfârșitul curbei în direcția punctului 0), obținem al doilea punct de evacuare de la drum, ceea ce indică o limită între grupele B și C. Aici, creșterea lină a valorilor totale caracteristice (grupa B) este înlocuită de o creștere extrem de slabă a semnului (grupa C).
Un exemplu cu o mașină ilustrează ideea unei metode, esența căreia poate fi clarificată prin simplificarea oarecum a problemei. Reprezentăm curba ABC sub forma unei compoziții de arce de trei cercuri (Figura 32): arcul LM al cercului O1, arcul MN. cercul O2. arc NP al cercului O3. Cea mai mare rază are un cerc O3. Raza cercului este O1, oarecum mai scurtă. Raza cercului O2 este substanțial mai scurtă. arcul al cărui MN se află în mijlocul figurii LMNP. Desenați o tangență la curba LMNP la punctul său inițial L și restaurați normalul din punctul de tangență în direcția centrului cercului O1. Lungimea normală trebuie să fie mai mare decât raza cercului O2. dar mai mici decât razele cercurilor O1 și O3 Să începem să mișcăm tangenta de la începutul până la sfârșitul curbei LMNP. Sfârșitul normalei va desena cifra lmnp. În secțiunile lm și np, capătul normal se mișcă într-o direcție cu tangenta, iar în secțiunea m se mișcă în direcția opusă. Punctele de pe curba lmnp, în care capătul direcției normale se schimbă, corespund punctelor de schimbare ale curburii figurii principale, adică LMNP.
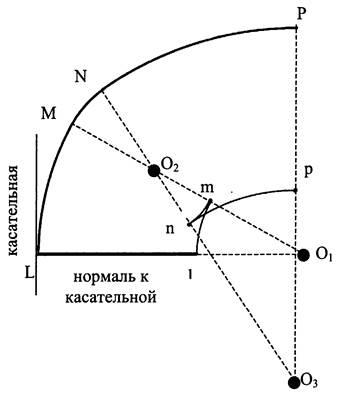
Fig. 32. Un exemplu de construire a unei buclă ABC
Curbele reale ABC constau din secțiuni elementare, fiecare caracterizată printr-o anumită curbură. Centrele de curbură a regiunilor elementare, de regulă, nu coincid una cu cealaltă, dar în regiunile A, B și C sunt relativ apropiate unele de altele, formând așa-numitele nori de centre de curbură.
Similar cu exemplul cu trei cercuri, trageți o tangență la curba ABC la punctul de pornire și restabiliți normalul în dreapta curbei. Lungimea normală este selectată, astfel încât nu a ajuns la setul de centrele de curbură corespunzătoare secțiunilor inițiale și finale ale programului, dar în același timp se extind dincolo de centrele mediane nor de curbură. Să mutăm tangenta de la începutul curbei până la sfârșitul graficului ABC. Evident că, în timp ce tangenta alunecă pe porțiunea cu rază mare de curbură (partea inițială a graficului, grupa A), un capăt normal situată între curba și centrele de curbură ale unui nor, se deplasează în direcția tangentei t. E. Rises. La momentul de intrare a tangenta la partea de mijloc a graficului cu rază mică de curbură de la sfârșitul direcției normale de circulație, prins în spatele unui nor de centre de curbură inversat. Sfârșitul normalelor începe să se deplaseze în stânga și în jos. punct curba care corespunde schimbării timpului direcției sfârșitului normale indică granița dintre grupele A și B. Mișcarea capătul descendent normal și la stânga, adică. e. în direcția opusă mișcării tangentei, se extinde la punctele de intrare tangente în secțiunea program de rectificare finală (aproximativ la "a zburat" de pe șosea a doua mașină). Aici, sfârșitul normalului, care se află între linia graficului și centrele de curbură, începe din nou să se miște în direcția tangentei. Punctul de pe curba la care există o schimbare repetată în direcția capătului normale, punctele de frontieră dintre grupele B și C. Nomenclatorul aici anunță asigurarea incrementului de circulație netede și începe nomenclatura în care fiecare dintre pozițiile dă o creștere foarte scăzută cifra de afaceri, adică nomenclatorul grupului C.
Forma finală a figurii, trasată de capătul normal al tangentei, atunci când aceasta se alunecă de-a lungul curbei ABC, este prezentată în Fig. 33.
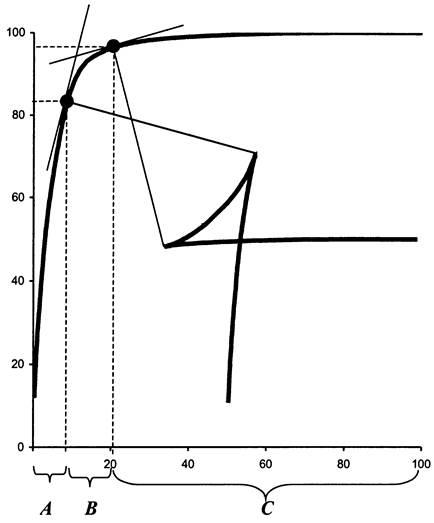
Fig. 33. Împărțirea în grupurile A. B și C cu ajutorul analizei ABC a buclei
Algoritmul pentru rezolvarea problemei utilizând instrumentele Excel este prezentat în Tabelul. 6.