Funcție complexă de transfer
Funcția de transfer este una din căile de descriere matematică a sistemului dinamic. Se utilizează în principal în teoria controlului, comunicării, procesării semnalelor digitale. Este un operator diferențial care exprimă legătura dintre intrarea și ieșirea unui sistem staționar liniar. Cunoscând semnalul de intrare al sistemului și funcția de transfer, puteți restabili semnalul de ieșire.
Funcția complexă de transfer (coeficientul de transfer, funcția sistemului) a circuitului determină răspunsul circuitului la acțiunea externă și este egal cu raportul dintre cantitatea de ieșire (tensiune, curent) și valoarea de intrare (tensiune, curent) exprimată în formă complexă.
Există patru tipuri de funcții de transfer:
1) funcția de transfer pentru tensiune:
2) funcția de transfer curent:
3) rezistența la transmisie:
4) conductivitatea transferului:
În general, funcția de transfer:
este reprezentat sub formă de AFC-K (# 969;) și PFC - # 966; (# 969;)
Dacă un semnal periodic al unei amplitudini și frecvențe date este alimentat la intrarea obiectului, atunci ieșirea va fi, de asemenea, un semnal periodic cu aceeași frecvență, dar în cazul general al unei alte amplitudini cu o schimbare de fază. Interrelația dintre parametrii semnalelor periodice la intrare și ieșire a obiectului determină caracteristicile de frecvență. Cel mai adesea ele sunt folosite pentru a descrie sisteme cu un singur canal:
Formal, răspunsul generalizat al frecvenței poate fi obținut din funcția de transfer prin înlocuirea lui p pentru
și este prezentată sub formă
.
Componentele răspunsului generalizat la frecvență au un înțeles independent și următoarele nume:
· Răspuns în frecvență reală (VCHH),
· Răspunsul imaginar de frecvență (MCH);
· Răspunsul frecvenței de amplitudine (AFC),
· Răspunsul la frecvența de fază (PFC).
Răspunsul de frecvență poate fi construit din expresia (2.42) pe planul complex. În acest caz, sfârșitul vectorului care corespunde unui număr complex. când se schimbă de la 0 la o curbă în planul complex, care se numește caracteristica fazei de amplitudine (AFC).
Un exemplu de caracteristică a fazei de amplitudine a unui sistem
Răspunsul la frecvența de fază (PFC) este o reprezentare grafică a schimbării de fază între semnalele de intrare și ieșire, în funcție de frecvență,
Pentru a determina numitorul și numitorul W (j) sunt factorizați nu mai mari decât ordinul doi
,
atunci. unde semnul "+" se referă la i = 1,2. l (la numitorul funcției de transfer), semnul "-" - la i = l + 1. L (numitorul funcției de transfer).
Fiecare dintre termeni este dat de
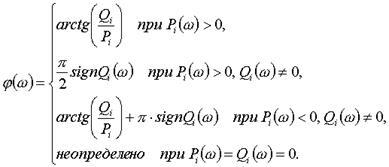
Răspunsul la frecvența amplitudinii (AFC) este o funcție care arată dependența modulului unei anumite funcții cu valoare complexă de frecvență. De asemenea, poate fi luată în considerare răspunsul de frecvență al altor funcții de frecvență complexe, de exemplu, densitatea spectrală a puterii semnalului.
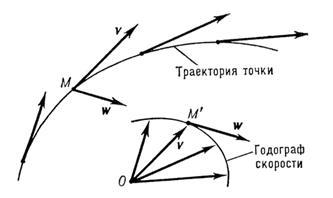
Hodograph este o curbă care reprezintă locusul geometric al capetelor unui vector variabil (variabil în timp), ale cărui valori la momente diferite sunt întârziate de originea comună
Hodograph oferă o reprezentare geometrică grafică a modului în care cantitatea fizică reprezentată de vectorul variabil se modifică în timp, iar rata acestei modificări, care este tangențială cu cea a hographografiei.
De exemplu, viteza unui punct este valoarea reprezentată de vectorul variabil v. După amânarea valorilor pe care vectorul v le are în momente diferite de timp, de la originea O, obținem curba de viteză a vitezei; În acest caz, cantitatea care caracterizează rapiditatea modificării vitezei la punctul M, adică accelerația (în acest moment), are pentru orice moment de timp direcția tangentei la viteza de viteză la punctul corespunzător M '.
Caracteristicile de frecvență ale rețelelor cu două terminale
Passive două terminale și patru stâlpi includ un set de elemente rezistive și reactive (inductive și capacitive) în care curge curenți electrici sub acțiunea unei singure surse de alimentare externă. Pentru a descrie fenomenele fizice care apar în astfel de circuite, atunci când sunt expuse la bornele de intrare ale unei surse de oscilații armonice cu frecvență fixă = const folosind metoda amplitudinilor complexe, care la rândul său, se bazează pe introducerea conceptelor de rezistențe complexe sau Conductanțele elemente individuale -r lanț. . . și amplitudinile complexe ale curenților și a tensiunilor -. .
În cazul general, sursa oscilațiilor armonice poate schimba nu numai amplitudinea și faza inițială, ci și frecvența unghiulară. Atunci caracteristica complexă a sursei (efect de intrare) este scrisă ca o funcție a variabilei complexe imaginare - (). Această caracteristică este de obicei scrisă în formă exponențială (polară) și se numește densitatea spectrală complexă. Modulul acestei caracteristici se numește densitatea spectrală, iar argumentul se numește densitatea de fază sau caracteristica de frecvență de fază. Deci, pentru tensiunea pe care o avem: