3-14 PROIECTE CONJECTARE
In contrast, o perspectivă și proiecții ortografice astfel încât proiecțiile sunt perpendiculare pe planul de proiecție, proiecția este formată prin proiecții paralele oblice cu centrul situată la infinit, și situat la un unghi oblic față de planul de proiecție. Schema totală de proiecție este prezentată în Fig. 3-20.
Proiecțiile oblice arată forma tridimensională generală a obiectului. Cu toate acestea, mărimea și forma reală sunt afișate numai pentru fețele obiectului care sunt paralele cu planul de proiecție, i. E. Unghiurile și lungimile sunt păstrate numai pentru astfel de fețe. De fapt, proiecția oblică a acestor fețe este echivalentă cu vederea ortografică din față. Marginile care nu sunt paralele cu planul de proiecție sunt distorsionate.
De interes deosebit sunt două proiecții oblice - Cavalierul și cabina de pilotaj. Proiecția cavalierului se obține atunci când unghiul dintre proiectoare și planul de proiecție este. În această proiecție, coeficienții de distorsiune pentru toate cele trei direcții principale sunt aceleași. Rezultatul acestei proiecții pare nefiresc îngroșat. Pentru a "corecta" acest neajuns, se utilizează proiecția cabinei.
Proiecția cabinei este o proiecție atât de oblică, pentru care coeficientul de distorsiune pentru marginile perpendiculare pe planul de proiecție este de 1/2. Așa cum se va arăta mai jos, pentru proiecția carlingii unghiul dintre proiectoare și planul de proiecție este.
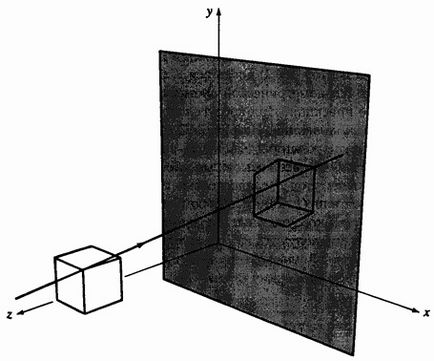
Fig. 3-20 Proiecția oblică.
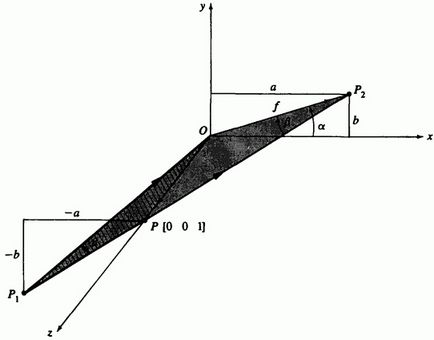
Fig. 3-21 Construcția unei proiecții oblice.
Pentru a construi o matrice de transformare pentru o proiecție oblică, ia în considerare vectorul unității de-a lungul axei arătate în Fig. 3-21. Pentru proiecția ortografică sau axonometrică pe plan, vectorul specifică direcția proiecției. Pentru o proiecție oblică, proiectorii formează un unghi cu planul de proiecție. În Fig. Figura 3-21 prezintă proiectorii cu unghi oblic tipic și. Proiectorii formează un unghi cu planul de proiecție. Rețineți că toți proiectorii posibili care trec printr-un punct sau formează un unghi cu un plan se află pe suprafața unui con cu vârf la sau. Astfel, pentru un anumit unghi există un număr infinit de proiecții oblice.
Proiectorul poate fi obținut prin utilizarea transferului punct-la-punct. Într-un plan bidimensional care trece prin axa perpendiculară, matricea transformării este
În spațiul tridimensional această transformare bidimensională este echivalentă cu schimbarea vectorului în direcțiile lui u. Pentru a face acest lucru, aveți nevoie de o conversie
Proiectul pe un plan oferă
Din fig. 3-21 că
unde este lungimea vectorului unitar proiectat pe axă, adică coeficientul de distorsiune și a este unghiul dintre axa orizontală și cea proiectată. Din fig. 3-21 este de asemenea clar că unghiul dintre proiectorii oblici și planul de proiecție este egal cu
Astfel, transformarea pentru proiecția oblică este:
Pentru că, obținem o proiecție ortografică. Dacă, atunci, muchiile perpendiculare pe planul de proiecție nu sunt distorsionate. Și aceasta este o condiție pentru proiectarea cavalierului. Din egalitate (3-43) avem:
Observăm că, în proiecție, cavalierul este încă un parametru liber. În Fig. 3-22 prezintă proiecția Cavalier pentru unele valori. Valori egale și cele mai des folosite. Valoarea este, de asemenea, utilizată.
Proiecția cabinei poate fi obținută cu un factor de distorsiune. De aici
În acest caz, din nou unghiul este o variabilă, așa cum se arată în Fig. 3.23. Valorile cele mai comune sunt și, de asemenea, valoarea este aplicată.
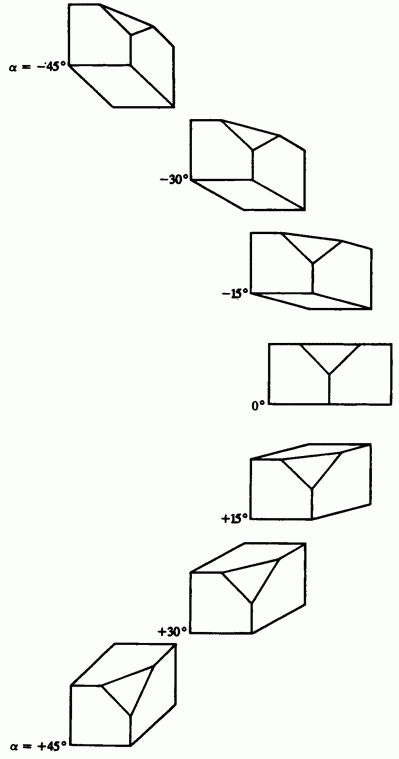
Fig. Proiecțiile lui Cavalier. De sus în jos, unghiul variază de la un interval până la un unghi.
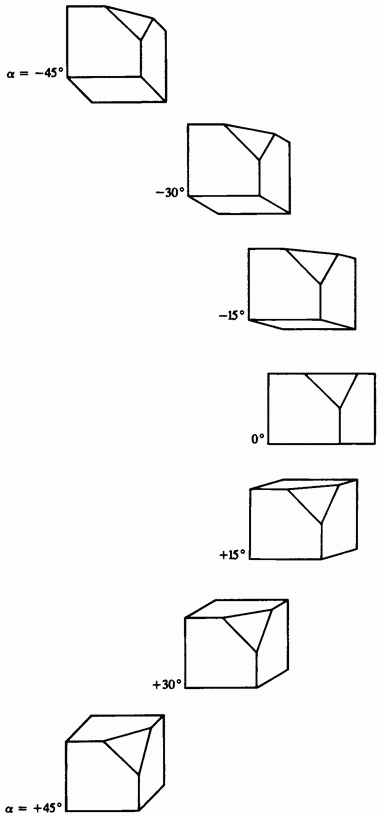
Fig. 3-23 Proiecțiile cabinei. De sus în jos, unghiul variază de la interval până la interval, coeficientul de distorsiune.

Fig. 3-24 Proiecții unghiulare înclinate. Din stânga la dreapta la.
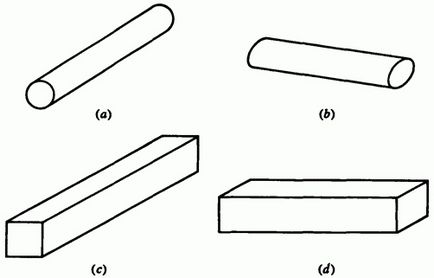
Fig. 3-25 Distorsiuni apărute în proiecții cu unghi oblic, ,,. (a) Fața rotundă este paralelă cu planul proiecției; (b) fața rotundă este perpendiculară pe planul proiecției; (c) partea lungă este perpendiculară pe planul de proiecție; (d) partea lungă este paralelă cu planul de proiecție.
În Fig. Figurile 3-24 prezintă proeminențe oblice pentru coeficienții de distorsiune cu un unghi.
Deoarece este reprezentată forma adevărată a unei fețe, proiecțiile oblice sunt deosebit de potrivite pentru a ilustra obiecte cu fețe rotunde sau alte fețe curbe. Aceste fețe trebuie să fie paralele cu planul de proiecție pentru a evita distorsiunile nedorite. La fel ca în cazul proiecțiilor paralele, obiectele cu o singură dimensiune substanțial superioare altora sunt supuse unei distorsiuni semnificative, cu excepția cazului în care această dimensiune este paralelă cu planul de proiecție. Astfel de efecte sunt prezentate în Fig. 3-25.
Următoarea este un exemplu detaliat.
Exemplul 3-16 Proiecții obișnuite
Construim proiecțiile unui cavalier și a unui compartiment pentru un cub cu un unghi de tăiere (vezi exemplul 3-13).
Reamintind că proiecția cavalierului este o proiecție oblică, adică coeficientul de distorsiune și selectarea unghiului pantei orizontale de la (3-44) obținem matricea de transformare
Transformăm coordonatele cubului cu unghiul de tăiere (vezi exemplul 3-13)
Rezultatul este arătat în Fig. 3-22.
Dacă ne întoarcem acum la proiecția cabinei și amintim că coeficientul de distorsiune este de 1/2, de la egalitatea (3-43) obținem
Selecționând din nou, din (3-44), avem:
Coordonatele de proiecție convertite pentru cub pentru acest cub sunt egale cu
Acest rezultat este prezentat în Fig. 3-23.
Rețineți că, atât pentru proiecția cavalierului, cât și pentru proiecția cabinei, fața triunghiulară nu este prezentată cu dimensiunile sau forma corectă, deoarece nu este paralelă cu planul de proiecție ().