Komsomolskaya Osh №5 І - ІІІ pași
SOLUȚII ALE EQUACAȚIILOR CARE CONȚIN SEMNUL DE MODUL
Rezolvarea ecuațiilor cu un modul cauzează dificultăți elevilor.
Analizând sarcinile examenelor de admitere, trebuie remarcat faptul că sarcinile cu module sunt adesea oferite. Pentru a ajuta studenții să învețe cum să rezolve ecuațiile cu module, acest material este oferit.
Ecuațiile cu modulul sunt împărțite în grupuri în funcție de modul în care sunt rezolvate. Fiecare material teoretic al grupului este dat. necesare pentru rezolvarea ecuațiilor unui anumit grup.
Soluțiile sunt date ecuațiilor fiecărui grup, iar ecuațiilor individuale un algoritm pentru rezolvarea acestora, care le permite elevilor să se autogineze.
Acest material poate fi folosit în lecții atunci când lucrează în grupuri și în mod individual atât în clasă, cât și pentru teme.
Este destinat studenților din clasele eradice.
Modulele care conțin variabila sub semnul modulului
Cele mai simple ecuații cu un modul sunt ecuațiile formei (1)
unde și sunt unele funcții.
Pentru a rezolva această ecuație, trebuie mai întâi să găsim toate soluțiile ecuației = aparținând setului, apoi să rezolvăm ecuația = pe set; Unirea seturilor de soluții găsite constituie setul tuturor soluțiilor de ecuație (1). Cu alte cuvinte, ecuația (1) este echivalentă cu setul de sisteme
Ecuația inițială este echivalentă cu setul de sisteme:
Răspuns. - 3; - 2; 2; 3.
Ecuația formei este echivalentă cu setul de sisteme (poate fi rezolvată în două moduri)
Această ecuație este echivalentă cu setul de sisteme:
Prin urmare, sistemul are o soluție.
Prin urmare, al doilea sistem are o soluție.
Ecuația formei, unde sunt anumite funcții, este echivalentă cu setul de sisteme
Această ecuație este echivalentă cu agregatul a două sisteme:
1). sistemul nu are soluții.
Când rezolvați o ecuație în care expresia care conține modulul se află sub semnul modulului, trebuie mai întâi să vă eliberați de modulele interne și apoi să deschideți modulele rămase în ecuațiile rezultate.
Această ecuație este echivalentă cu agregatul a două sisteme
adică un set de sisteme
Al doilea sistem nu are soluții. Primul sistem este echivalent cu următoarele două sisteme:
5. Metoda de împărțire în intervale. O ecuație a formei (2)
Se rezolvă prin metoda intervalelor (sau prin metoda de împărțire în intervale). Pentru a face acest lucru, ei găsesc mai întâi toate punctele în care
Aceste puncte împart regiunea valorilor admisibile ale ecuației (2) în intervale, în fiecare dintre acestea toate funcțiile păstrează semnul (presupunem semnul fiecărui modul la intervalul indicat). Apoi trec din ecuația (2) și setul de sisteme care nu conțin semnele modulului.
18. Găsiți toate rădăcinile ecuației care satisfac inegalitatea.
RĂSPUNSURI ȘI SOLUȚII.
2. Utilizați metoda de defalcare.
CU MODULUL CARE CONȚINE PARAMETRUL.
1. Pentru fiecare valoare a parametrului, găsiți numărul rădăcinilor ecuației.
Soluția. Vom scrie ecuația în formă, deoarece nu este o rădăcină a ecuației. Numărul rădăcinilor acestei ecuații va corespunde numărului de puncte de intersecție a graficului funcției cu linia dreaptă. Construim un grafic al funcției, care constă din două părți:
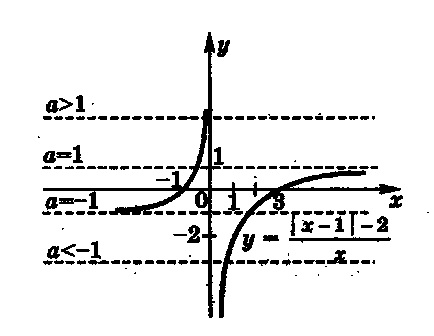
Se poate vedea din figura asta
are un singur punct de intersecție și, prin urmare, o singură rădăcină;
are două puncte de intersecție și, prin urmare, ecuația inițială are două rădăcini;
la un punct de intersecție și, prin urmare, ecuația are o singură rădăcină.
Rămâne să verificăm cât de multe rădăcini are ecuația inițială pentru u.
Să presupunem că atunci ecuația inițială ia forma. Să determinăm numărul de rădăcini ale ecuației date.
Fie, atunci avem următoarea ecuație:
Răspuns: când ecuația are o singură rădăcină;
când ecuația are două rădăcini;
ecuația are o soluție unică.
2. Pentru fiecare valoare a parametrului, găsiți numărul rădăcinilor ecuației.
Soluția. Rescrim ecuația în formă.
Pentru a rezolva problema, definim numărul punctelor de intersecție a graficului funcției u. Construim graficul funcției
care constă din două părți:
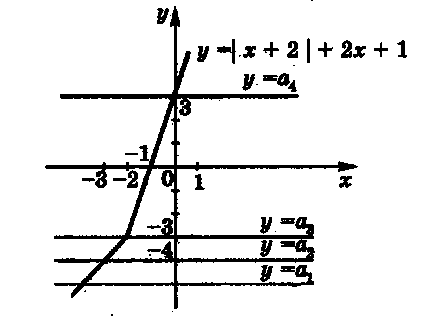
Se poate vedea din figură că pentru orice valoare a parametrului ecuația inițială are o rădăcină.
Răspuns: pentru orice valoare a parametrului, ecuația inițială are o rădăcină.
3. Pentru ce valori ale parametrului face ecuația
Are cel puțin o soluție?
Soluția. Funcția de submodule
Dacă, atunci, de atunci, și egalitatea este realizată doar cu, adică.
Dacă, atunci, egalitatea se realizează numai atunci când.
Deci, pentru toți. Deoarece, atunci ecuația (1) este echivalentă cu sistemul și numai pentru valorile parametrului găsit ecuația inițială are o soluție,
1. Pentru fiecare valoare a parametrului, găsiți numărul rădăcinilor ecuației
2. Pentru fiecare valoare a parametrului, găsiți numărul rădăcinilor ecuației
3. Pentru ce valori ale parametrului ecuația are cel puțin o soluție?
1. Când o ecuație are o singură rădăcină;
când ecuația are două rădăcini.
2. Pentru orice valoare a parametrului, ecuația are o singură rădăcină.