Un cerc este o curbă a planului închis, toate punctele fiind la fel de îndepărtate de un anumit punct (centru). Dacă R - raza unui cerc - distanța de la fiecare punct la centrul său, atunci circumferința este exprimată prin numărul 2PR, iar zona delimitată de aceasta, numărul pR 2. unde p = 3,14159 - raportul dintre circumferința și diametrul său.
Ecuația unui cerc într-un sistem de coordonate dreptunghiular:
unde, c și d sunt coordonatele centrului.
Rețineți că mișcarea circulară este adesea găsit în fizica și tehnologia, pe un traseu circular atunci când se deplasează oamenii de echitatie pe carusel roata Ferris, de-a lungul orbite circulare se pot muta sateliți artificiali. Modelul planetar al atomului de hidrogen din Rutherford este bine cunoscut. În centrul atomului este nucleul, iar electronul se învârte în jurul lui.
Elipsă (elleipsis greacă -. Lipsa) - linia de intersecție a unui con circular drept cu un plan, care nu trece prin vârful conului și se intersectează toate formând drept o cavitate a conului.
Mijlocul 0 al segmentului F1F2 (lungime focală) se numește centrul elipsei.
Într-o formă dreptunghiulară de coordonate 0hu sistem cu originea în centrul elipsei, pe care se află axa 0x focarele elipsei ecuației elipsei este de forma
unde a și b sunt lungimile semiaxelor mari și mici ale elipsei. Pentru a = b, focurile F1 și F2 coincid, iar această ecuație definește un cerc, care este considerat un caz special al unei elipse.
Elipsa este o linie centrală a ordinii a doua.
Elipsa este o linie închisă simetrică pe axele axelor 0x și 0yight (mari și mici) și centru.
Forma elipsei ("alungirea" ei) este determinată de excentricitatea e = c / a<1 (для окружности е=0 )
Direct D1 D1 „și D2 D2“ (figura 1), paralelă cu axa mică a elipsei și distanțate față de centrul său, la o distanță d = ± a / e. sunt numite direcții de elipse, focare corespunzătoare F1 și F2. Raportul dintre distanțele de orice punct al elipsei și distanța până la focalizarea corespunzătoare directricea sale este constantă și egală cu excentricitatea r1 / d1 = r2 / d2 = e. Zona elipsei este S = pi * a * c. pi = 3,14159.
Rețineți că planetele din jurul Soarelui se deplasează de-a lungul elipse.
Numele "Ellipse" a fost introdus de Apollonius din Perga, considerând elipsa ca fiind una dintre secțiunile conice.
Parabola (parabola greacă) este o curbă a ordinii a doua.
O linie dreaptă o intersectează la cel mult două puncte.
În acest caz, parabola poate fi definită ca.
-setul de puncte M (xy) al planului a cărui distanță FM față de un anumit punct F al acestui plan (centrul parabolei) este egală cu distanța MN cu o anumită dreaptă AN - direcția directă a parabolei;
-linia de intersecție a unui con circular drept cu un plan care nu trece prin vârful conului și paralel cu un anumit plan tangent al acestui con;
-într-o formă dreptunghiulară de coordonate 0hu sistem care pornește de la vârful parabolei și axa direcționată de-a lungul axei ecuatia parabolei 0x parabolei are o forma așa-numita canonic
unde p (parametru focal) este distanța de la focalizare la regizor.
Observăm că, de-a lungul parabolei, corpul se mișcă într-un câmp omogen de gravitate, turnat la un unghi la orizont, și o particulă încărcată într-un câmp electric omogen de condensator plat.
Hyperbole (hiperbola greaca) este o linie curba plata;
Mijlocul 0 al segmentului F1F2 (lungime focală) este numit centrul hiperboliei;
- linia de intersecție a unui con circular drept cu un plan care nu trece prin vârful conului și intersectează ambele cavități;
- 0hu în coordonate rectangulare cu originea în centrul hiperbola pe care se află axa 0x focii a ecuației hiperbolă a hiperbola are o așa-numită canonic
unde a și b sunt lungimile semicelor hiperboliei.
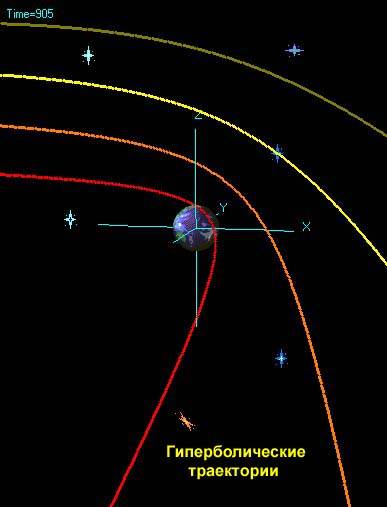
Rețineți că hiperbola este în mișcare corpuri care părăsesc Pământul pentru totdeauna, viteza căreia este mai mare decât a doua cosmică (11,2 km / s). De asemenea, particulele de Alfa se deplasează de-a lungul hiperboliei în experimentul Rutherford atunci când sunt împrăștiate de nucleul atomului.