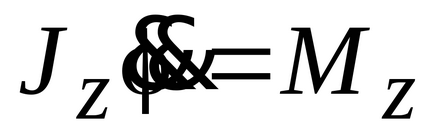Luați în considerare un sistem mecanic cu constrângeri ideale. Fie forțele active ale sistemului. Să dăm sistemului mecanic o deplasare virtuală și să calculam activitatea elementară a forțelor sistemului asupra acestei deplasări:
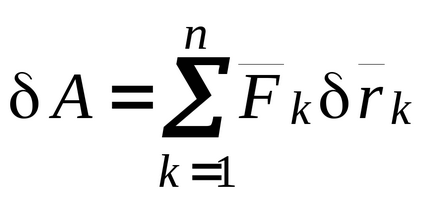
Folosind egalitatea (17.2), exprimăm variația
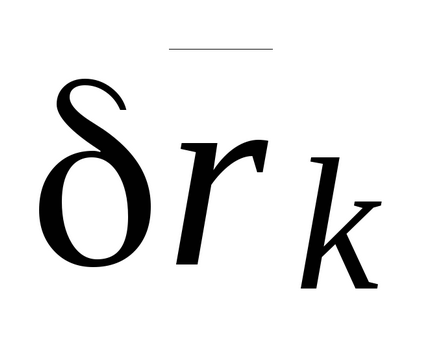
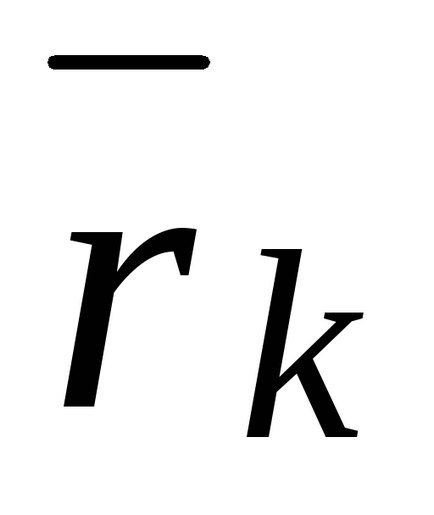
Sa schimbam ordinea sumarii in (17.6):
În expresia (17.7)
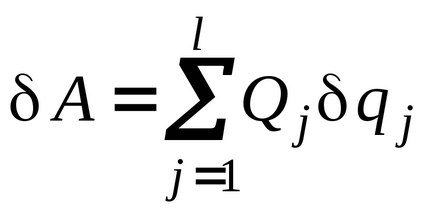
Forțele generalizate Qj sunt numite coeficienți pentru variațiile coordonatelor generalizate în expresia lucrării elementare a forțelor sistemului.
În funcție de dimensionalitatea variațiilor coordonatelor generalizate
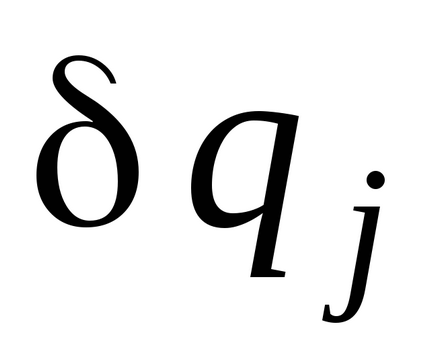
Metode de calcul al forțelor generalizate
Să analizăm trei moduri de calcul al forțelor generalizate.
1. Definiția forțelor generalizate prin formula de bază (17.8)
Formula (17.9) este rar utilizată în practică. La rezolvarea problemelor, este adesea folosită a doua metodă.
2. O metodă de "înghețare" a coordonatelor generalizate.
Să dăm un sistem mecanic de deplasare virtuală, în care excepția sunt toate variațiile de coordonate generalizate
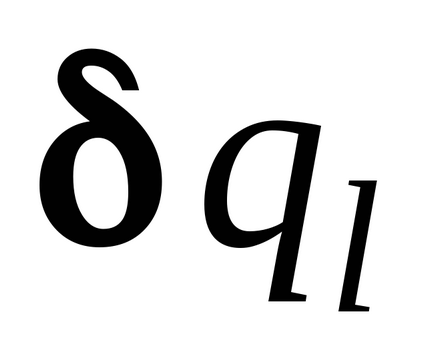
.
Calculați această operațiune de deplasare
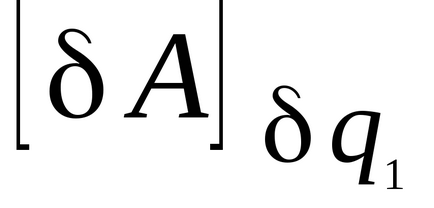
.
Prin definiție, factorul de variație
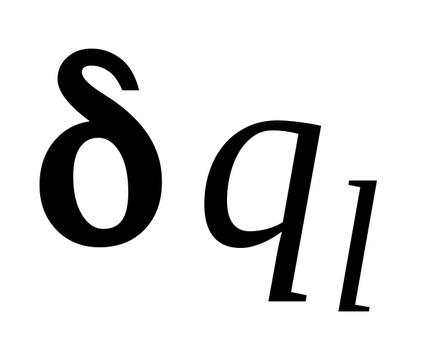
Apoi, dăm sistemului o deplasare virtuală
și definește a doua forță generalizată Q2. calcularea muncii virtuale a tuturor forțelor sistemului
.
În mod similar, calculăm toate celelalte forțe generalizate ale sistemului.
3. Cazul unui potențial câmp de forță.
Să presupunem că energia potențială a unui sistem mecanic
.
Apoi și utilizând formula (32.8)
Principiul mișcărilor statice virtuale în coordonatele generalizate
Conform principiului deplasărilor virtuale ale staticilor pentru echilibrul unui sistem cu retenție ideală, conexiuni staționare, este necesar și suficient ca starea
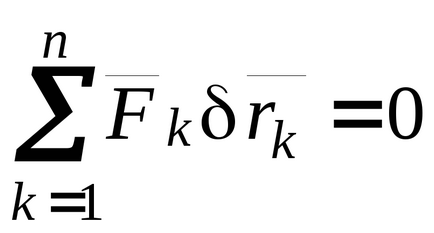
Trecând la coordonatele generalizate, obținem
Deoarece variațiile coordonatelor generalizate sunt independente, egalitatea expresiei (17.11) la zero este posibilă numai în cazul în care toți coeficienții din variațiile coordonatelor generalizate sunt zero:
Astfel, într-un sistem mecanic cu ideale, holonomic, staționare și link-ul de susținere este în echilibru dacă și numai dacă toate forțele sistemului generalizate sunt zero (zero la viteza inițială a sistemului).
Ecuațiile Lagrange în coordonate generalizate (ecuațiile Lagrange de al doilea tip)
Ecuațiile Lagrange derivă din ecuația generală a dinamicii prin înlocuirea deplasărilor virtuale prin expresiile lor în termeni de variații ale coordonatelor generalizate. Ele sunt un sistem de ecuații diferențiale de mișcare a unui sistem mecanic în coordonate generalizate:
unde
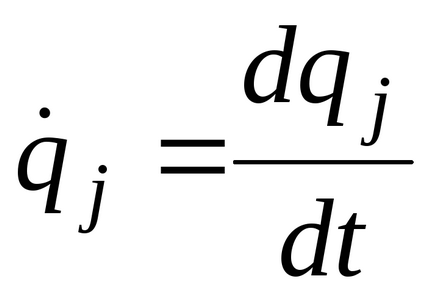
T energia cinetică a sistemului, reprezentată ca o funcție a coordonatelor generalizate și a vitezelor generalizate
,
Numărul de ecuații ale sistemului (17.13) este determinat de numărul de grade de libertate și nu depinde de numărul de corpuri care intră în sistem. Cu conexiuni ideale, numai forțele active vor intra în partea dreaptă a ecuațiilor. Dacă conexiunile nu sunt ideale, atunci reacțiile lor trebuie atribuite forțelor active.
În cazul forțelor potențiale care acționează asupra sistemului mecanic, ecuațiile (17.13) iau forma
.
Dacă introducem L Lagrangiene = T P. este dată că energia potențială este independent de vitezele generalizate, obținem ecuațiile Lagrange al doilea tip, în cazul forțelor potențiale în forma următoare
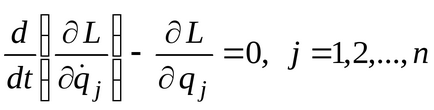
La elaborarea ecuațiilor Lagrange de al doilea fel trebuie efectuate următoarele acțiuni:
Setați numărul de grade de libertate ale unui sistem mecanic și alegeți coordonatele sale generalizate.
Formularea expresiei energiei cinetice a sistemului și prezentarea acestuia ca o funcție a coordonatelor generalizate și a vitezelor generalizate.
Folosind metodele descrise mai sus pentru a găsi forțele active generalizate ale sistemului.
Efectuați toate operațiile de diferențiere necesare în ecuațiile Lagrange.
Să compunem ecuația diferențială a mișcării de rotație a unui corp rigid sub acțiunea unui sistem de forțe active (figura 17.3) conform algoritmului de mai sus.
1. Un organism care efectuează o mișcare de rotație are un grad de libertate. Pentru coordonata generalizată luăm unghiul :
2. Energia cinetică a corpului în timp ce se rotește în jurul axei fixe este egală cu
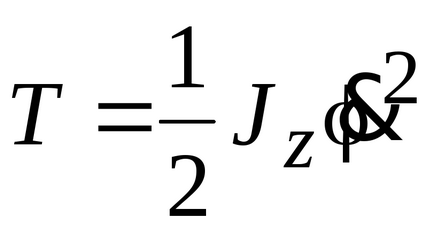
unde Jz este momentul inerției corpului în raport cu axa de rotație z.
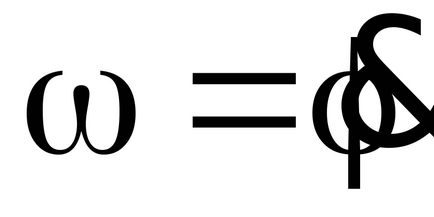
3. Definirea forței generalizate. Să dăm organismului o deplasare virtuală și să calculam activitatea virtuală a tuturor forțelor active ale sistemului:
.
În consecință, Q = Mz este momentul principal al forțelor active ale sistemului față de axa de rotație a corpului.
4. Efectuăm operațiile de diferențiere în ecuația Lagrange
Substituind egalitatea (17.15) în ecuația (173
14) obținem ecuația diferențială a mișcării de rotație a corpului