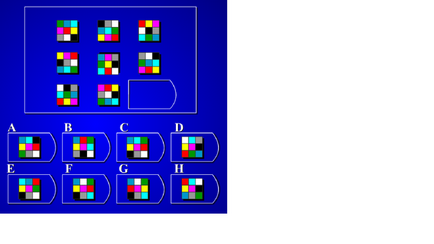
Înainte să vă imaginați. Partea superioară a acesteia ar trebui să fie de nouă pătrate de dimensiunea 3x3. Dar numai ultimul, patratul 9 (care ar trebui să fie în colțul din dreapta jos) este tăiat, și vedeți doar opt. Fiecare pătrat 3x3 este alcătuit din nouă pătrate mici colorate. Există nouă culori diferite, în fiecare pătrat 3x3 sunt toate cele nouă. Asta e doar ordinea aranjamentului acestor culori de fiecare dată când este diferit.
Care pătrat a fost tăiat în colțul din dreapta jos? Vi se oferă opt opțiuni, le vedeți în partea de jos a imaginii. Care dintre ele va fi adevărat, cum vor fi cele nouă pătrate mici (și de ce)?
bonus pentru cel mai bun răspuns (emis): 5 credite
Răspunsul corect este C.
Vizualizăm modelele de aranjare a pătratelor colorate într-o pătrată de 3x3.
Distingem trei grupe de culori:
- Negru, alb, gri
- Verde, albastru, albastru
- Purpuriu, roșu, galben.
Să începem cu primul grup. În cele opt pătrate cunoscute, grupul "gri" este localizat peste tot într-o singură linie: orizontal sau vertical. Și nicăieri patratele nu formează un unghi sau în linii diferite.
Această condiție este satisfăcută de patratele B, C, E.
Acum să luăm în considerare același lucru pentru grupul "roșu".
Vedem că sub forma unei linii "grupul roșu" este de la deja selectat (B, C, E) numai în C pătrat.
Pentru verificare, vom verifica și "grupul verde". Ea se termină și în S.
Deci, răspunsul este un pătrat sub simbolul C.
O mare sarcină pentru logica și respectarea nivelului clasei a VI-a a vremurilor sovietice.