Shenyagin A.S. BTSM-111
În stadiul actual al dezvoltării tehnologiei, este mult mai convenabil și mai fiabil să se utilizeze receptoare cu procesare digitală a semnalelor. Digitizarea semnalului RF este împiedicată direct, deoarece circuitele digitale moderne nu au adesea un răspuns rapid care să satisfacă condițiile teoremei Kotel'nikov-Shannon. Sa spus mai sus că anvelopa complexă conține toate informațiile necesare pentru decodarea semnalului și calcularea puterii și caracteristicilor sale de fază. Plicul complex al semnalelor de bandă îngustă este o pereche de semnale de frecvență joasă, care sunt convenabile pentru digitizare (fără a încălca condițiile teoremei Kotelnikov).
Pentru a extrage un plic complex de semnal, se utilizează procedura de heterodynizare. Esența lui este după cum urmează. RF semnal de intrare s (t) = A (t) ∙ cos (ω0 ∙ t + φ (t)) este multiplicat cu oscilația celor două oscilatoare (LO) la o ω0 frecvență, deplasată în fază una în raport cu cealaltă printr-un unghi π / 2 - cos (ω0 ∙ t) și -sin (ω0 ∙ t).
s (t) ∙ cos (ω0 ∙ t) = A (t) ∙ cos (ω0 ∙ t + φ (t)) ∙ cos (ω0 ∙ t)
A (t) ∙ cos (φ (t)) + 0,5 ∙ A (t) ∙ cos (2ω0 · t + φ (t)
s (t) (sin (ω0 · t)) = - A (t) ∙ cos (ω0 · t + φ (t)) ∙ sin (ω0 ∙ t)
(∞) ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ =
0,5 ∙ q (t) - 0,5 ∙ A (t) ∙ sin (2ω0 · t + φ (t)) (2)
Din formulele (1) și (2), care conțin rezultatele multiplicări a două componente - o frecvență mică de 0,5 ∙ i (t) și 0,5 ∙ q (t), care sunt reale și imaginare părți ale învelișului complex de înaltă frecvență și 0,5 ∙ A (t) ∙ cos (2ω0 ∙ t + φ (t)) și -0,5 ∙ A (t) ∙ sin (2ω0 ∙ t + φ (t)), care poate fi îndepărtată prin filtrul trece jos (LPF) . Figurile 1-2 prezintă diagramele unui demodulator de tip quadrature (vector) cu un schimbător de faze și fără un schimbător de faze.
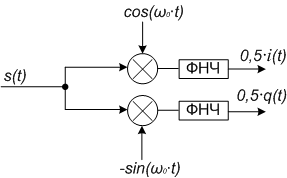
Figura 1 - Diagrama funcțională a demodulatorului vectorial
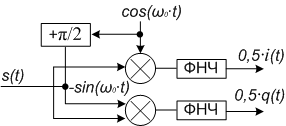
Figura 2 - Diagrama funcțională a unui demodulator vector cu un schimbător de fază
Vector demodulator descrisă prin formulele (1) și (2), care primesc o vedere „frumoasă“, numai în cazul în care semnalul de referință de oscilator local este identic în frecvență și fază inițială a unei ω0 oscilație de referință (adică, semnalul de undă purtătoare și oscilatorul local receptorul sunt coerente). Această condiție poate fi realizată prin utilizarea servo sistemelor construite pe baza circuitelor cu buclă blocată în fază (PLL). În cazul în care acest lucru nu este prevăzut, ieșirea demodulatorului cuadratură avem două componente ale așa-numitele beat-uri, a căror frecvență depinde de receptor heterodine de frecvență de eroare și frecvența purtătoare a semnalului recepționat. Neconcordanța dintre faza inițială a heterodynei receptorului și frecvența purtătoare a semnalului recepționat va distorsiona nivelele proiecțiilor de cvadratură. În acest caz, spunem că plicul complex al semnalului este obținut în raport cu frecvența ωg.
Să descriem situația matematic. Fie frecvența heterodyne a receptorului ωg = ω0 + δ, faza inițială este φg. apoi:
s (t) ∙ cos (ωg ∙ t) = A (t) ∙ cos (ω0 ∙ t + φ (t)) ∙ cos (ωg ∙ t + φg)
A (t) ∙ 0,5 ∙ cos (ω0 ∙ t + φ (t) + ωg ∙ t + φg) + A (t) ∙ 0,5 ∙ cos (ω0 ∙ t + φ (t) - ωg ∙ t -φg) = ...
Grupăm termenii sub cosinus, separând separat termenul φ (t) și extinzându-i în funcție de formulele pentru adăugarea argumentelor:
= A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ cos ((ω0 + ωg) ∙ t + φg) -.
-A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ sin ((ω0 + ωg) ∙ t + φg) + ...
+A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ cos ((ωg - ω0) ∙ t + φg) + ...
+A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ sin ((ωg - ω0) ∙ t + φg) = ...
Deoarece ωg = ω0 + δω
= A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ cos ((2 ∙ ω0 + δω) ∙ t + φg) -.
-A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ sin ((2 ∙ ω0 + δω) ∙ t + φg) +.
+ A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ cos (δ ∙ t + φg) + ...
+ A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ sin (δ ∙ t + φg) = ...
= 0,5 ∙ i (t) ∙ cos ((2 ∙ ω0 + δω) ∙ t + φg) -.
-0,5 ∙ q (t) ∙ sin ((2 ∙ ω0 + δω) ∙ t + φg) + ...
+0.5 ∙ i (t) ∙ cos (δ ∙ t + φg) + ...
+0,5 ∙ q (t) ∙ sin (δ ∙ t + φg)
După LPF, avem
Ib (t) = 0,5 ∙ i (t) ∙ cos (δ ∙ t + φg) + 0,5 ∙ q (t) ∙ sin (δ ∙ t + φg)
s (t) ∙ sin (ωg ∙ t) = A (t) ∙ cos (ω0 ∙ t + φ (t)) ∙ sin (ωg ∙ t + φg) =.
A (t) ∙ 0,5 ∙ sin (ω0 ∙ t + φ (t) + ωg ∙ t + φg) + A (t) ∙ 0,5 ∙ sin (ωg ∙ t + φg - ω0 ∙ t -φ ( t)) =.
Grupăm termenii sub cosinus, separând separat termenul φ (t) și extinzându-i în funcție de formulele de adăugare a argumentelor:
= A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ cos ((ω0 + ωg) ∙ t + φg) +.
+ A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ sin ((ω0 + ωg) ∙ t + φg) +.
+ A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ sin ((ωg - ω0) ∙ t + φg) - ...
- A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ cos ((ωg - ω0) ∙ t + φg) = ...
Deoarece ωg = ω0 + δω
= A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ cos ((2 ∙ ω0 + δω) ∙ t + φg) +.
+A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ sin ((2 ∙ ω0 + δω) ∙ t + φg) +.
+ A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ sin (δ ∙ t + φg) -.
- A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ cos (δ ∙ t + φg) =.
= 0,5 ∙ q (t) ∙ cos ((2 ∙ ω0 + δω) ∙ t + φg) +.
+0.5 ∙ i (t) ∙ sin ((2 ∙ ω0 + δω) ∙ t + φg) +.
+ 0,5 ∙ i (t) ∙ cos (δ ∙ t + φg) -.
- 0,5 ∙ q (t) ∙ sin (δ ∙ t + φg)
= - 0,5 ∙ q (t) ∙ cos ((2 ∙ ω0 + δω) ∙ t + φg) -.
- 0,5 ∙ i (t) ∙ sin ((2 ∙ ω0 + δω) ∙ t + φg) -.
- 0,5 ∙ i (t) ∙ cos (δ ∙ t + φg) +.
+ 0,5 ∙ q (t) ∙ sin (δ ∙ t + φg)
După LPF, avem
Qb (t) = 0,5 ∙ q (t) ∙ cos (δ ∙ t + φg) - 0,5 ∙ i (t) ∙ sin (δ ∙ t + φg)
Astfel, la ieșirea demodulatorului cu cadre avem două semnale
Ib (t) = 0,5 ∙ i (t) ∙ cos (δ ∙ t + φg) + 0,5 ∙ q (t) ∙ sin (δ ∙ t + φg)
Qb (t) = 0,5 ∙ q (t) ∙ cos (δ ∙ t + φg) - 0,5 ∙ i (t) ∙ sin (δ ∙ t + φg)