În metoda LU-factorizare (această schemă este denumită schema gaussiană compactă), următoarea secvență de acțiuni se efectuează la rezolvarea sistemului.
Matricea este reprezentată ca o lucrare
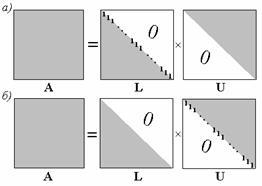
Fig. 2.3. Structura matricelor L și U din Dulittl (a) și Kraut (b)
unde L este matricea triunghiulară inferioară, U este matricea triunghiulară superioară. Această descompunere este unic cu alegerea prealabilă a unuia dintre elementele diagonale ale matricelor. În acest caz, numărul de elemente din matricea A coincide cu numărul total al elementelor necunoscute ale matricelor L și U. Dacă unitatea este primită L diagonală, o astfel de descompunere se numește descompunerea Doolittle Dacă unitatea U diagonală (figura 2.3, a.) - descompunerea Kraut (Figura 2.3. , b). În viitor, în construirea metodei LU-factorizare, vom folosi descompunerea Kraut.
Sistemul este înlocuit de sistem
ușor de rezolvat în două etape:
Pasul 1. Luând în considerare forma triunghiulară a matricei L., nu este dificil să se obțină acest lucru în algoritmul Kraut
Pasul 2. Soluția acestui sistem în algoritmul lui Kraut:
Costurile totale pentru implementarea ambilor pași pentru n >> 1 sunt operațiuni lungi.
Obținem relațiile pentru calculul elementelor matricelor L și U în algoritmul Krautt. Pentru a face acest lucru, multiplicăm matricele L și U și echivalăm rezultatul cu A. Prin regula de multiplicare a matricelor
Luați în considerare elementul (Figura 2.4) situat pe diagonala centrală sau în partea triunghiulară inferioară a matricei A. Pentru un astfel de element i ≥ j. Din figura aceasta rezultă
Fig. 2.4. Ilustrație a calculului elementului matrice situat
sub diagonala principală
deoarece i ≥ j și. De aici
Luați în considerare elementul (figura 2.5), situat deasupra principalului
Fig. 2.5. Ilustrație a calculului elementului matrice situat
deasupra diagonalei principale
diagonală a matricei A (pentru ea j> i). În acest caz
Am primit ca urmare a unor raporturi care permit să se calculeze elementele matricelor L și U. Secvența de calcul: prima coloană a matricei este calculat L. U. în continuare rând al matricei și apoi coloana matrice L. din nou rând suplimentar al matricei U, și așa mai departe (vezi figura 2.6 .... care ilustrează secvența de calcule și schema de stocare a matricelor L și U).
Calculul coloanei matricei L și rândul matricei U se numește etapa descompunerii LU. Să dăm un exemplu de schemă de stocare pentru elementele matricelor A, L, U după al doilea pas al descompunerii LU (Figura 2.7).
Numărul de operații aritmetice lungi în etapa de descompunere a LU pentru n >> 1 este o valoare. la etapa de decizie
sisteme cu matrice triunghiulare. Numărul total al operațiunilor lungi este aproximativ egal (ca în metoda Gauss),
Fig. 2.6. Matricea inițială A (a), schema de stocare L și U a matricelor (b), secvența de calcul a elementului din schema de stocare primită (c)
Fig. 2.7 Schema de depozitare a elementelor 4'4 ale matricelor A, L, U după a doua etapă a factorizării LU
.. Aceasta este, principalele costuri cad pe LU-factorizarea A. Această caracteristică face o metodă deosebit de atractivă a LU-factorizare de rezolvare a sistemelor liniare cu aceeași matrice A. dar diferite părți din dreapta face:
În acest caz, factorizarea matricei se realizează o singură dată, necesitând operațiuni lungi, iar soluția fiecărui sistem cu partea dreaptă corespunzătoare este realizată pentru astfel de operațiuni.
punerea în aplicare extrem de eficientă a metodei LU-factorizare poate fi obținută dacă vom restricționa clasa sistemelor liniare cu simetrică pozitiv matrice bine definit A. t. E. O astfel de implementare se numește prin metoda Cholesky sau de rădăcină pătrată.
Presupunem că sistemul care trebuie rezolvat
are o matrice simetrică pozitivă simetrică A. În acest caz, matricea A este reprezentată în formă
Aici este matricea triunghiulară inferioară. O astfel de descompunere există și este unică pentru matricile simetrice definite definitiv.
Sistemul este transformat în formă
Vectorul este căutat printr-o soluție secvențială de două sisteme cu matrice triunghiulare:
Pentru a obține relațiile calculate ale elementelor matricei, considerăm un element arbitrar al matricei A:
Suma aici este efectuată numai până la j. t. la. Selectați termenul pentru valoarea k = j:
Aceste relații ne permit să calculam elementele matricei prin coloane.
Eficacitatea acestei metode se realizează în stadiul de extindere a matricei, deoarece în acest caz trebuie calculată numai matricea. Costurile aritmetice în metoda Cholesky constituie operațiuni lungi și n operații pentru extragerea rădăcinii pătrate.
Există o altă variantă a descompunerii unei matrici simetrice pozitive definite, în care este posibil să se evite operațiile de extragere a unei rădăcini pătrate. În această variantă, o nouă matrice este introdusă conform regulii
și - matricea, calculată anterior de schema Cholesky, este o matrice diagonală cu elemente de matrice. Matricea există și este triunghiulară inferioară cu unitatea diagonală. În acest caz
Relațiile calculate pentru elementele matricelor u pot fi obținute, ca și mai înainte, prin aplicarea regulii de multiplicare a matricelor
din care rezultă că
deoarece matricea are o unitate diagonală.
Un astfel de algoritm va necesita dubla multiplicare ca si schema Cholesky. Totuși, dacă introducem o schimbare a variabilelor
atunci relațiile calculate vor lua forma
Aici se calculează mai întâi cantitățile auxiliare. și apoi sunt utilizate pentru a determina cantitățile necunoscute și. Numărul de multiplicări cu o astfel de organizare a algoritmului este aproximativ și nu conține o operație de extracție a rădăcinii pătrate.