În această lucrare, timpul este măsurat direct
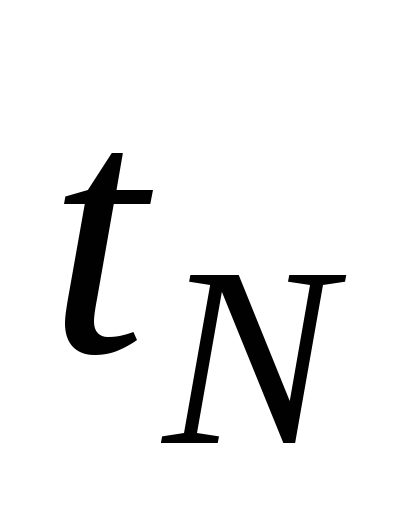
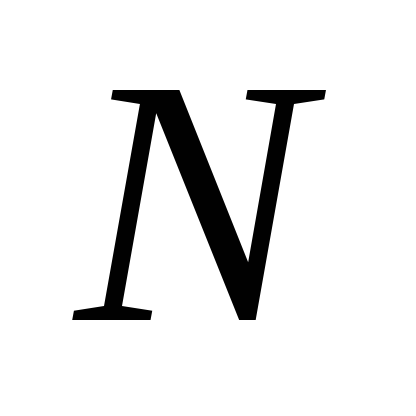
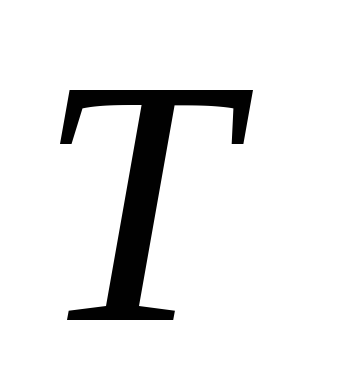
Astfel, din timpul măsurat
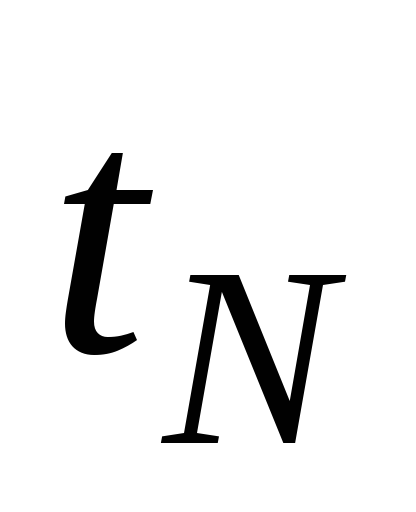
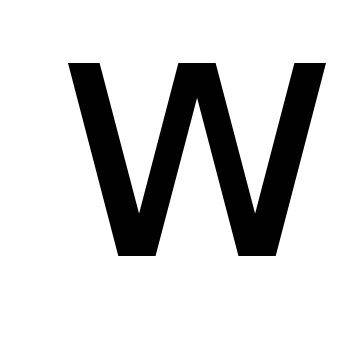
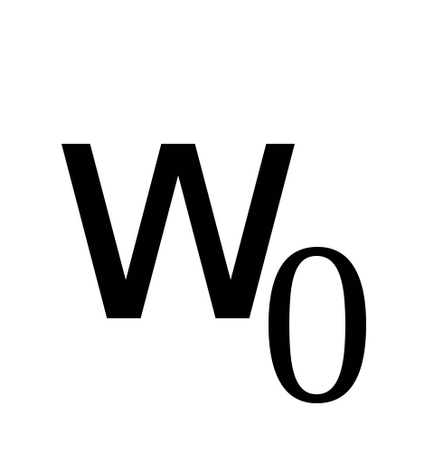



eroare
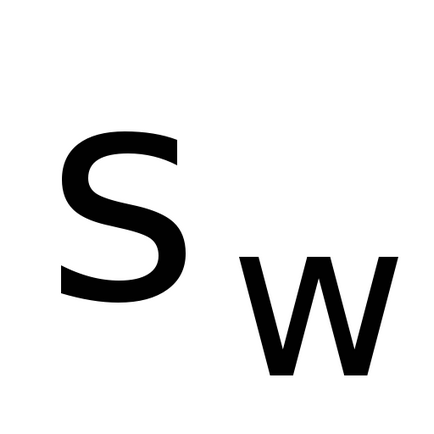
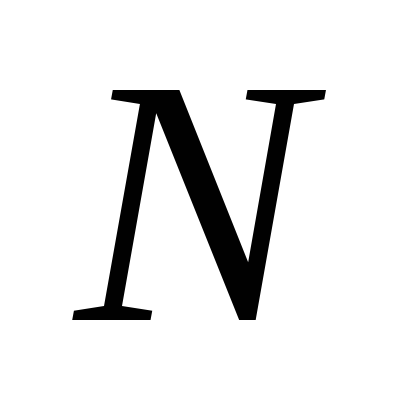
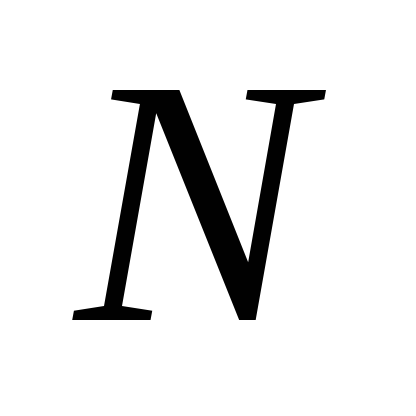
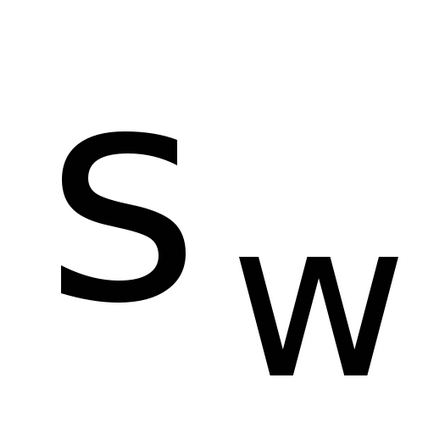
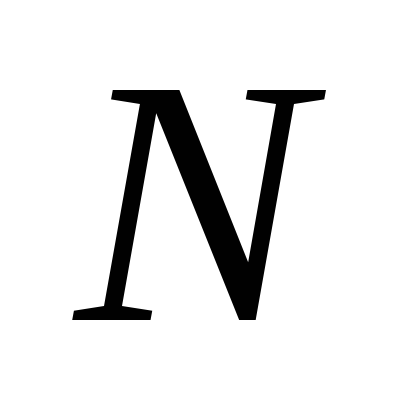
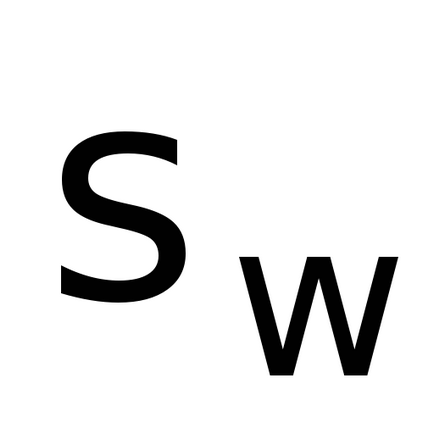
Teoretic discutat modelul Deformarea unghiurile pendulului din poziția de echilibru presupus a fi mici (ipotezele (1) și (2)), astfel încât atunci când lucrarea de laborator trebuie amintit că deformarea maximă unghiurile pendule ar trebui să fie nu mai mult, de exemplu, 10 de grade.
Vă recomandăm să luați următoarele valori pentru numărul de oscilații observate:
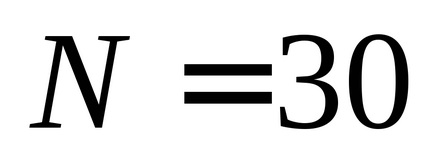
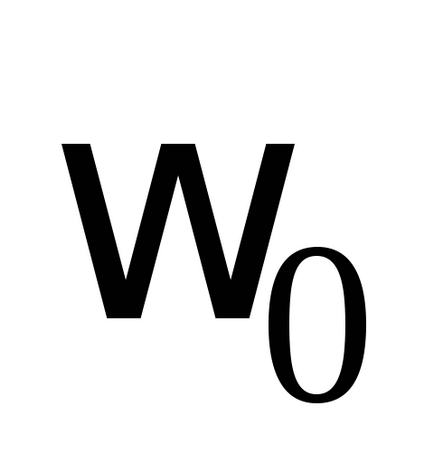
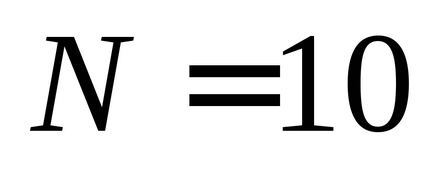


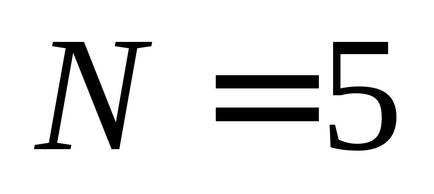

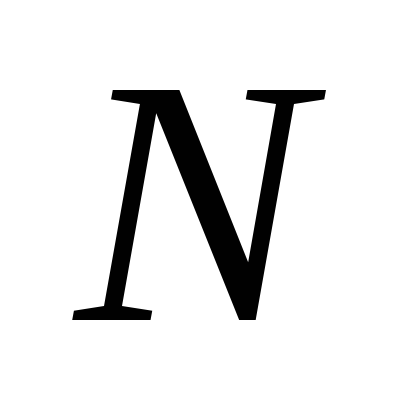
Activitate de laborator
Scoateți arcul. Măsurați frecvențele
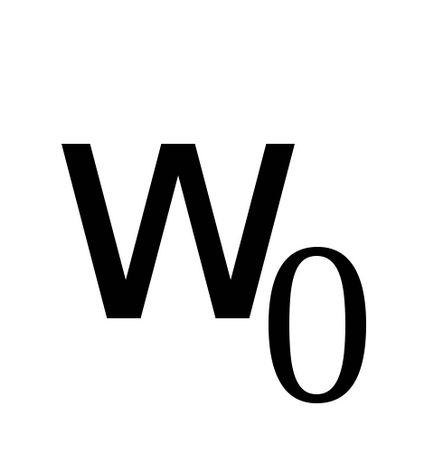
Setați arcul (prima poziție, cea inferioară, poziția arcului este setată de către instructor). Măsurați frecvențele oscilațiilor normale



Efectuați pasul 2 al sarcinii pentru alte patru poziții de arc, ridicându-l în sus.
Calculați frecvența bate

Pe baza rezultatelor lucrării, trage concluzii cu privire la valabilitatea următoarelor predicții teoretice:
despre egalitatea de frecvență aproximativă

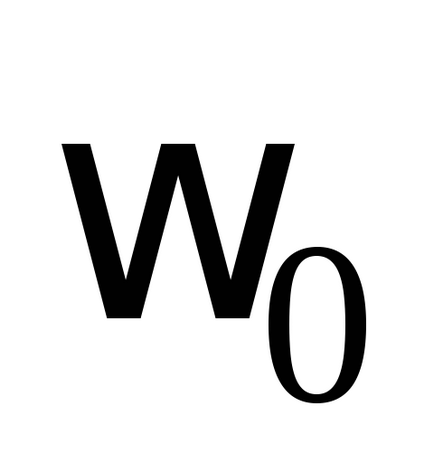
privind independența frecvenței

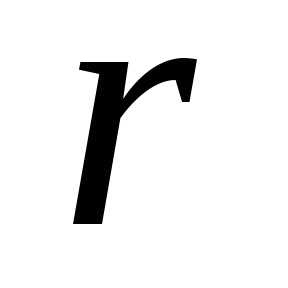
despre creșterea frecvenței

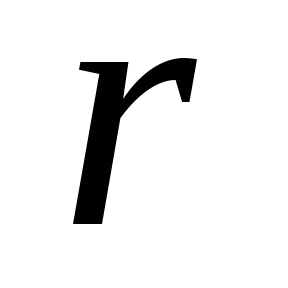
privind egalitatea frecvenței batei

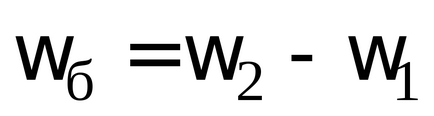
la creșterea frecvenței batei

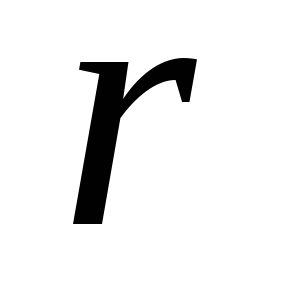
Pentru aceste constatări fac mai evidente, își prezintă rezultatele în cadrul incertitudinilor de măsurare grafic în ușor de citit și de a compara forma de pre-a decide problema ce să amâne axele.
Întrebări de test
Care este scopul lucrării?
Ce formule funcționează?
Ce veți măsura direct?
Ce veți determina în mod indirect?
Cum veți măsura frecvențele vibrațiilor normale și frecvența bate?
Ce dependențe grafice așteptați să obțineți? Ce ați decis să amânați de-a lungul axelor de coordonate?
Cum veți calcula erorile tuturor cantităților?
Ați dedus formulele corespunzătoare pentru calcularea erorilor corespunzătoare?
Cum se determină numărul de grade de libertate?
Cum este scris ecuația fundamentală a dinamicii mișcării de rotație?
Cum sunt derivate ecuațiile (4) și (5)?
Când ecuațiile (7), (8) intră în ecuațiile oscilațiilor armonice?
Ce oscilații sunt numite normal?
Ca de la poziția normală (18) pentru a obține soluția de ecuațiile (7) și (8), în forma (10), (11)?
Care este fenomenul de batai?
Când are loc acest fenomen?
De ce bătăile nu sunt vibrații armonice?
Care este amplitudinea ritmului? Desenați un grafic al amplitudinii bătăilor versus timp.
De ce funcție de frecvența bătăilor egală cu diferența de frecvență dintre normal, în loc de jumătățile, înregistrat în formulele (25), (26) și (32), (33)?
Ce se întâmplă cu energia pendulurilor în procesul bătăilor?
Rezultatele dvs. teoretice confirmă concluziile teoretice?