1. Luați în considerare câmpul gravitațional al unei mase de puncte m plasate la originea O (0,0,0). Un astfel de câmp este descris de o funcție de vector. unde # 947; - constanta gravitațională; - vectorul de rază al punctului. . Cu o astfel de forță acționează un câmp pe unitate de masă, plasat într-un punct. Câmpul gravitațional este potențial. Acesta poate fi reprezentat ca un gradient al unei funcții scalare. numit potențialul newtonian al câmpului gravitațional al masei punctuale m. De fapt:
2. Câmpul de încărcare a punctului electric e, plasat la origine, este descris în punctul de vectorul de stres. (.) Acest câmp este potențial. Acesta poate fi reprezentat ca un gradient al unei funcții scalare. care se numește potențialul câmpului electric al încărcării punctului e.
Definiția 8. Suprafețele de nivel (liniile de nivel pentru un câmp plan) ale unui potențial se numesc suprafețe equipotențiale (linii).
Rețineți că o suprafață equipotențială (linie) și o linie de vector care trece printr-un punct comun. sunt reciproc ortogonale în ea.
Exemplu 13. Verificați dacă câmpul este potențial. Dacă este, atunci găsiți potențialul câmpului, construiți liniile equipotențiale și liniile de câmp vectorial. Selectați vectorul și liniile equipotențiale care trec prin punct.
Soluția. Câmpul este definit pe întregul plan XOY.
Să verificăm dacă sunt îndeplinite condițiile necesare și suficiente pentru potențialitate: domeniu potențial.
1. Pentru a găsi funcția, vom compila sistemul :.
Din prima ecuație, integrând-o peste variabila x. găsi:
.(Rolul unei constante aici este jucat de orice funcție care depinde de x). Pentru a găsi, înlocuim funcția găsită în a doua ecuație a sistemului:
2. Condiția de echilibru potențial. . prin urmare, obținem o familie de linii echipotențiale.
Reducem ecuația în forma canonică:
Aceasta este o familie de hyperbola la.
În cazul în care. obținem ecuațiile liniilor.
Construim linii echipotențiale în planul XOY.
3. Linia vectorului câmpului. Să compunem ecuația diferențială a liniilor vectoriale de câmp: Să o rezolvăm.
- familie de hiperbola, dacă. și două linii drepte. în cazul în care. Construim liniile vectoriale în planul XOY.
Liniile equipotențiale și vectoriale la punctele de intersecție sunt ortogonale. Să verificăm acest lucru pentru liniile care trec printr-un punct.
4. Vom da coordonatele punctului din ecuația liniilor vectoriale :. O linie vectorială trece prin punctul M.
În mod similar, găsim pentru o linie echipotențială care trece prin punctul M. O linie echipotențială trece prin punctul M.
Calculam panta tangentelor la aceste curbe la punctul M:
Pentru linia vectorului: în M :.
Pentru o linie echipotențială în T. M :.
- starea de perpendicularitate a două tangente.
Concluzie: vectorul și liniile equipotențiale la punctul M sunt ortogonale.
Exemplul 14. Asigurați-vă că câmpul este potențial, găsiți potențialul câmpului și calculați lucrul efectuat de acest câmp atunci când mutați un punct material de la.
Soluția. Pentru a răspunde la întrebarea potențialului unui anumit domeniu, calculăm derivatele parțiale ale funcțiilor. . . Aceste funcții sunt continuu împreună cu derivatele lor parțiale în orice moment.
Vedem că sunt îndeplinite condițiile necesare și suficiente pentru potențialul domeniului. . . . ore, etc.
Pentru a calcula potențialul, folosim faptul că integrarea liniară într-un astfel de câmp nu depinde de calea integrării și poate fi calculată din formula Newton-Leibniz. Permiteți punctului să fie începutul căii, iar unele indică sfârșitul căii. Calculam integrala peste conturul format din segmente de linii drepte paralele cu axele de coordonate (vezi Figura 10). .
Ecuațiile părților contur :. . .
. x este fixat aici, prin urmare,
. aici y este fix. prin urmare,.
Ca rezultat, obținem :.
Acum se calculează același integral prin formula lui Newton-Leibniz. = =.
Din egalitatea obținută rezultă acest lucru. Potențialul acestui domeniu este găsit.
Găsiți lucrarea făcută de câmpul vectorial atunci când mutați un punct de la. Într-un câmp potențial, lucrarea este egală cu diferența potențială la punctele finale și inițiale ale căii,
Exemplul 15. Verificați potențialul unui câmp vectorial. găsiți ecuațiile suprafețelor equipotențiale și selectați printre ele una care trece prin punctul M (2,1,1).
Soluția. Câmpul este definit în fiecare punct al spațiului. Să verificăm potențialul câmpului (a se vedea (11)):
condițiile sunt îndeplinite, câmpul este potențial. Puteți găsi potențialul în același mod ca în exemplul 12, dar într-un mod diferit. Pentru a găsi potențialul, avem sistemul:
Integrarea primei ecuații a sistemului în raport cu variabila x. vom găsi. Diferențiezăm expresia rezultantă cu privire la y: Din cea de-a doua ecuație a sistemului, obținem: Expresia exactă pentru potențial:
. Diferențăm în raport cu variabila z și o comparăm cu a treia ecuație a sistemului :.
Restaurați întreaga funcție :. Potențialul este găsit.
După ce a cerut. obținem ecuațiile de suprafețe equipotențiale:
Reducem această ecuație în forma canonică :.
Acestea sunt ecuațiile de sfere cu centrul O (0; 1; 1) și raza
Găsim o suprafață echipotențială care trece prin punctul M (2,1,1). Înlocuim coordonatele unui punct în ecuația unei suprafețe, definim:
prin punctul M trece sfera.
Gasim linia vectorială a câmpului care trece prin punctul M.
Ecuațiile liniilor vectoriale:
în M :, adică, o linie dreaptă trece prin M. pentru că acesta trece prin centrul sferei, planul tangent la sfera din m. M este perpendicular pe el. Adică, linia vectorului și suprafața equipotențială în M sunt reciproc ortogonale.
Direcția de mișcare a câmpului de-a lungul acestei linii coincide cu direcția axei OX pentru x> 0 și este opusă acestuia pentru x<0. Это совпадает с направлением увеличения потенциала U. Действительно, чем больше потенциал, тем больше радиус сферы.
Benchmark 6.
1. Verificați dacă câmpul vector este potențial. Găsiți potențialul său. Desenați linii de potențial egal. Găsiți liniile vectoriale și le trageți în aceeași figură. Calculați lucrul câmpului atunci când mutați punctul de material de la punctul la. Găsiți linia vectorială și linia echipotențială care trece prin punct.
2. Verificați dacă câmpul vectorial este potențial. Dacă da, găsiți potențialul său.
3. Găsiți potențialul câmpului gravitațional.
4. Arătați că câmpul vector este potențial și căutați potențialul său.
Fluxul unui câmp vectorial.
lăsa # 963; - o suprafață orientată în regiunea G. Alegem o anumită parte a acesteia, dând un vector unic al normalei la suprafață.
Fluxul unui vector printr-o suprafață # 963; este integrale de suprafață a produsului scalar al vectorului de câmp de vectorul unitar normal: n. (13)
Există alte forme de înregistrare a fluxului unui vector. De exemplu, luând în considerare faptul că obținem: П.
Sau puteți defini un vector. direcționate de-a lungul normalei la suprafață, astfel încât: . Apoi :. (14)
Dacă suprafața este închisă, atunci de obicei direcția exteriorului normal la suprafață este luată ca direcția vectorului și este marcată cu
Dacă schimbăm orientarea (luăm cealaltă parte a suprafeței), atunci produsul scalar și, respectiv, semnul de schimbare a fluxului.
Fluxul poate fi scris într-o formă de coordonate, reprezentând produsul scalar al vectorilor u:
unde pe partea dreaptă avem o suprafață integrală a celui de-al doilea tip.
Fiecare dintre termenii din formula (17) este transformat într-un integral dublu pe domeniul D. care este proiecția suprafeței # 963; pe planul corespunzător de coordonate:
unde sunt proiecțiile # 963; pe planurile de coordonate Oyz, Oxz, Oxy, respectiv. Semnul înainte de integrarea dublă pe partea dreaptă coincide cu semnul cosinus al unghiului dintre vectorul normal și suprafața și direcția pozitivă a axelor Ox, Oy, Oz. Expresiile sunt obținute prin exprimarea variabilelor de la ecuația de suprafață # 963;:. Este posibil să se reducă calculul fluxului la calculul integral al primului tip, înlocuind în formula (16). . .
Exemplul 16. Calculați fluxul unui câmp vectorial printr-o parte a planului. închis în primul octant, spre normal, formând un unghi obtuz cu axa OY.
Prin formula (13). unde # 963; - plan S :.
Reamintim că vectorul normal la planul cu ecuația are forma. În sarcina noastră. acest vector formează un unghi ascuțit cu axa OY. Apoi.
Reducem problema la calculul integral al primului tip (vezi (13)).
Dar. și anume . Din algebra vectorului se știe că aria triunghiului MNP (a se vedea figura 12) Răspuns :.
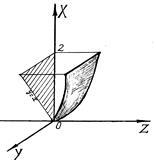
Găsiți fluxul unui câmp vectorial printr-o parte a suprafeței. dacă vectorul normal de la suprafață este un unghi ascuțit cu direcția pozitivă a axei OX.
Soluția. Să compunem integralul pentru calculul fluxului câmpului:
Din Figura 12 vedem că vectorul face un unghi ascuțit cu OX, cu OY o linie dreaptă, cu OZ un unghi abrupt, deci.
Calculăm. Proiecția liniei de intersecție și pe planul YOZ :. Apoi: Din ecuația de suprafață. atunci
Calculăm. Din ecuația de suprafață. atunci
Rezultatul poate fi verificat prin reducerea problemei la un element de suprafață integrat de primul tip. Pentru aceasta, găsim direcția cosine și calculam. Dacă ecuația suprafeței are forma. atunci vectorul este normal pentru el. a.
În exemplul (15), ecuația de suprafață :. Având în vedere că vectorul normal este un unghi ascuțit cu axa OX. noi avem. Apoi.
Pentru a calcula acest integrat de primul tip, proiectăm # 963; pe planul XOY (vezi Figura 12), apoi:
Din ecuația de suprafață. . .
Sarcina de control 7.
1. Gasiti fluxul unui camp vector printr-un paraboloid in doua moduri, folosind formulele (15) si (17).
2. Calculați fluxul unui câmp vectorial printr-o suprafață orientată # 963; dacă: a) # 963; - o parte din suprafața conică. normalul este extern; b) # 963; - parte a avionului. .
3. Calculați fluxul unui câmp vectorial printr-o parte a sferei.