Pentru vectorii geometrici, produsul scalar este determinat prin caracteristicile geometrice și este introdus după cum urmează:
Această expresie poate fi rescrisă în termeni de coordonate (aici formula pentru spațiul tridimensional):
4.) Colinaritatea și coplanaritatea
Vectorii paralele cu o linie sau situate pe o linie sunt numite vectori coliniari
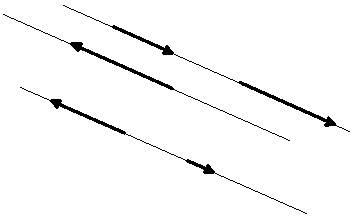
Condițiile de colinearitate pentru vectori
Două vectori vor fi coliniari dacă oricare dintre aceste condiții este îndeplinită:
1. Doi vectori a și b sunt coliniari dacă există un număr n astfel încât
2. Două vectori sunt coliniari dacă rapoartele coordonatelor lor sunt egale.
N.B. Condiția 2 nu este aplicabilă dacă una din componentele vectorului este zero.
3. Două vectori sunt coliniari dacă produsul lor vectorial este egal cu vectorul zero. Produsul vectorial al doi vectori a = și b = într-un sistem de coordonate carteziene este un vector a cărui valoare poate fi calculată folosind următoarele formule: a x b = matrice i j k ax ay az bx cu bz sau a x b =
N.B. Condiția 3 se aplică numai pentru problemele tridimensionale (spațiale).
Trei vectori (sau mai mulți) sunt numiți coplanari dacă aceștia, fiind redus la originea comună, se află în același plan.
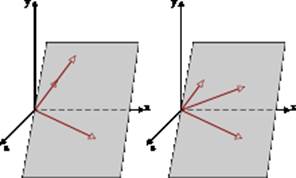
Să fie vectorii spațiului. Apoi următoarele afirmații sunt adevărate:
1. Dacă cel puțin unul dintre cei trei vectori este zero, atunci trei vectori sunt, de asemenea, considerați coplanari.
2. Un vector de vectori care conțin o pereche de vectori coliniari este coplanar.
3. Un produs mixt de vectori coplanari. Acesta este un criteriu pentru coplanaritatea a trei vectori.
Vectorii coplanari sunt dependenți liniar. Acesta este, de asemenea, un criteriu pentru coplanaritate.
4.Există numere reale, cum ar fi pentru coplanar. cu excepția cazurilor sau. Aceasta este o reformulare a proprietății anterioare și, de asemenea, un criteriu pentru coplanaritate.
5. În spațiul tridimensional se formează 3 vectori noncoplanari. Adică, orice vector poate fi reprezentat ca: Apoi vor fi coordonate pe această bază.