Ultimele știri
Problema aranjamentului reginelor. Reîncercați cu întoarcere.
Problema aranjamentului reginelor.
Un mic indiciu pentru rezolvarea problemei aranjamentului a 8 regine.
Esența problemei. A fost necesar să se găsească astfel de aranjamente de opt regine pe o șahă obișnuită, astfel încât să nu se bată unul pe celălalt.
Trebuie remarcat imediat că nu putem sorta toate variantele posibile ale constelațiilor. Mai exact, puteți scrie cu siguranță un astfel de program, dar vom face altfel, mai optim.
Unele observații privind modul de păstrare a aranjamentului.
Să vedem cum vom stoca locația reginei pe tablă. Soluția evidentă ar fi aceea de a crea o matrice de 8X8 și de a scrie unul sau zero în ea, în funcție de faptul dacă celula este ocupată de regină sau nu.
Dar să ne gândim, chiar avem nevoie de întreaga tablă? Se pare că nu. Îți aducem aminte cum umblă regina. Pentru orice număr de celule de-a lungul verticale, orizontale sau diagonale. Evident, dacă există o regină pe o anumită axă verticală, atunci o altă regină nu va fi pusă pe această linie verticală, deoarece se vor bate unii pe alții.
Este logic să stocați numai o gamă unidimensională de opt elemente, fiecare dintre acestea corespunzând unei verticale. Valoarea fiecărui element va corespunde liniei în care este instalată regina. Următoarea figură explică perfect acest principiu.
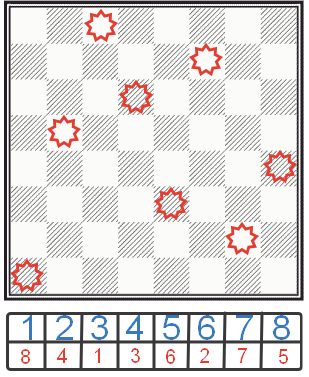
Despre verificarea dacă câmpul este "sub luptă" sau nu.
Să descriem matematic ce celule de șah sunt "sub lupta" reginei, instalate în celulă [i] [j].
Uită-te la figura următoare.
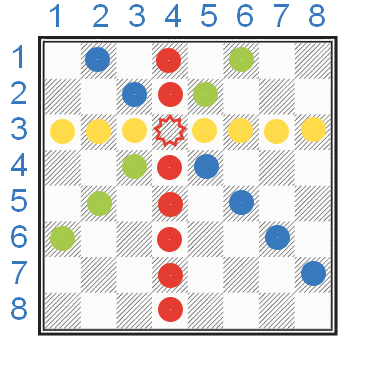
Aceste condiții pot fi schimbate cu ușurință în modul nostru de stocare a reginelor.
Să spunem că există deja mai multe dame care nu se lovesc reciproc. Ce condiții se impun următoarei regine?
Este clar că trebuie să procesați în mod consecvent fiecare dintre elementele anterioare. Să vrem să punem regina pe poziția k.
Începem testul, cu primul element, în care avem valoarea opt. Prin urmare, k nu trebuie să fie egală cu opt, în caz contrar ambele regine vor fi pe aceeași linie orizontală. În plus, k + 4! = 8 + 1 (starea liniei verde), altfel încercăm să punem regina pe diagonala ocupată. Și în cele din urmă, k-4! = 8-1 (condiția liniei albastre), în caz contrar vom cădea din nou pe diagonală, care bate cealaltă regină. Nu este necesar să verificați starea liniei roșii, deoarece modul de reprezentare a constelațiilor din memorie nu va permite ca două regine să fie plasate pe o linie orizontală.
Verificări similare vor fi necesare pentru toate reginele care au fost deja instalate pe placă. Este logic să alocăm aceste verificări unei funcții care are două argumente - șirul și coloana celulă în care dorim să instalăm regina.
Algoritmul de bază al soluției. Reîncercați cu întoarcere.
Acum vom discuta algoritmul de bază care realizează aranjamentul reginelor. Vom acționa așa cum am proceda dacă am avea o adevărată bord în fața ochilor noștri.
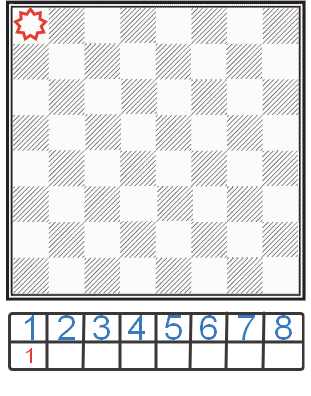
Puneți prima regină în prima celulă a primei verticale. În consecință, în primul element al matricei noastre, salvăm identitatea. Ei bine, prima regină este instalată. Este timpul să încercați să instalați a doua regină.
Trebuie să stea pe al doilea orizontal.
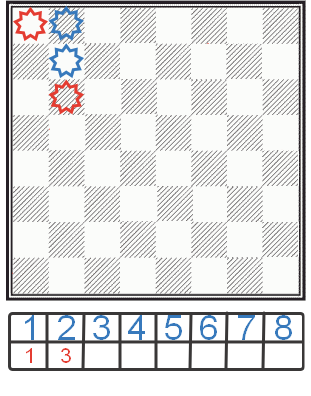
Să verificăm cea de-a doua celulă, a doua pe verticală. Rezultatul verificării este nesatisfăcător, acest câmp bate și regina stabilită anterior.
Acum vom verifica cea de-a treia colivie a celui de-al doilea vertical, poate că ne va potrivi? Într-adevăr se potrivesc. Am instalat regina acolo. Continuăm să instalăm a treia regină pe a treia verticală.
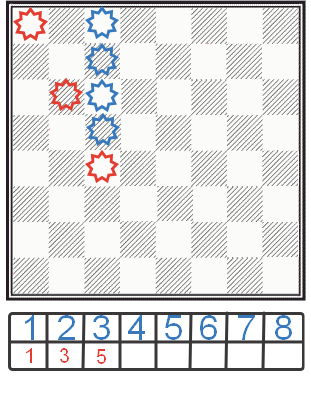
Începem testul cu o celulă a celui de-al treilea vertical.
Cred că este deja evident că nici primul, nici cel de-al doilea, nici cel de-al treilea, nici cel de-al patrulea ne vor potrivi, deoarece sunt bătuți de regine stabilite anterior. Dar cea de-a cincea celulă va fi exactă, deoarece nici prima, nici a doua regină nu sunt bătuți. Deci, ne-am stabilit a treia regină acolo.
În mod similar, vom umple verticalele a patra, a cincea, a șasea și a șaptea. Până în prezent, toate acestea pot fi implementate printr-o căutare standard în două cicluri. Bucla exterioară se mișcă vertical de la 1 la 8, iar cea interioară se mișcă orizontal.
În mod separat, ia în considerare instalarea reginei pe ultima verticală.
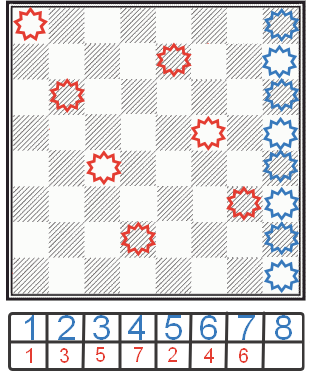
Dacă ați făcut totul în conformitate cu algoritmul, atunci la acest pas veți obține situația prezentată în figura din dreapta. Se pare că regina actuală nu are unde să instaleze, deoarece toate celulele din această linie verticală sunt bătute de cele șapte dame stabilite anterior.
Ce ar trebui să fac? Este necesar să se întoarcă un pas și să încerce să se stabilească a șaptea regină într-un alt loc.
Această operație se numește retur.
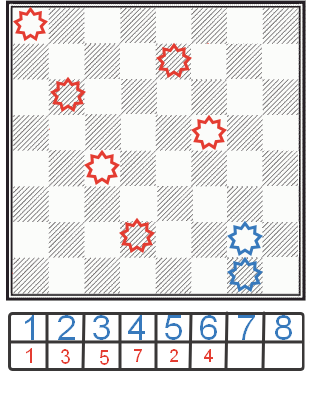
Vom verifica numai celulele de la 5 la 8. Este ușor de văzut că nici unul dintre ele nu este potrivit. Deci, vom face o revenire mai mult și vom încerca să instalăm a cincea regină într-un loc nou.
Verificați, după cum probabil ați ghicit deja, vom începe cu a treia celulă a celui de-al cincilea vertical. Nu va funcționa pentru noi, pentru că este în luptă și de la două regine la o dată, de la al doilea și al treilea. Dar a patra cușcă este liberă și, prin urmare, în ea vom paria regina noastră.
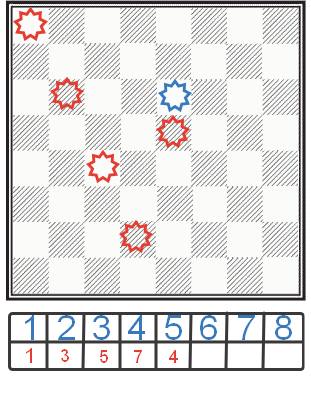
Continuând în acest spirit (alternând cu setarea cu întoarcere), mai devreme sau mai târziu ne vom împiedica pe un astfel de aranjament de regine care să îndeplinească toate cerințele noastre. Cu alte cuvinte, 8 regine vor fi plasate pe bord, care nu se vor bate unul pe altul. Dacă am dat peste un astfel de aranjament, îl vom salva într-o matrice separată sau îl vom putea afișa imediat pe ecran. După aceasta, va trebui să continuăm căutarea.
Acesta este un indiciu uriaș. Folosind cunoștințele dobândite, încercați acum să scrieți programul corespunzător.