Starea activității:
O minge cântărind 0,15 kg lovește un perete neted, la un unghi de 30 ° față de el și se zbate fără să piardă viteza. Găsiți forța medie care acționează asupra mingii din partea laterală a peretelui, dacă viteza mingii este de 10 m / s, iar durata grevei este de 0,1 s.
Numărul de sarcină 2.1.37 din "Colectarea problemelor de pregătire pentru examenele de admitere în fizică ale UGNTU"
\ (M = 0,15 \) kg, \ (\ alpha = 30 ^ \ Circ \) \ (\ Upsilon = 10 \) m / s, \ (\ Delta t = 0,1 \) c \ ( F-A \)
Soluția problemei:
În această formulă, \ (\ Delta p \) - o minge de impuls schimbare a fost lovit de zid, \ (\ Delta t \) - condițiile cunoscute ale interacțiunii.
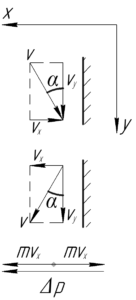
Să găsim schimbarea în ritmul mingii. Figura arată momentele imediat înainte de impact și imediat după impact. Deoarece nu există pierderi de viteză, impactul este considerat a fi absolut elastic, astfel încât mingea va sări în același unghi. Proiectăm viteza mingii înainte și după impactul pe axa \ (x \) și \ (y \).
Se vede că de-a lungul axei \ (y \) (\ upsilon_y \) viteza de proiecție \ egal, înainte și după impact \ (\ Upsilon \ cos \ alpha \), prin urmare, își schimbă pulsul minge în această direcție nu a fost, și mijloace în acest sens și nu există nici o forță.
Pe axa \ (x \) modulul de schimbare a impulsului va fi (vezi partea de jos a circuitului):
\ [\ Delta p = 2m = 2m \ Upsilon \ păcatul \ alpha \; \; \; \; (2) \]
Înlocuim (2) în (1), obținem soluția problemei într-o formă generală.
Substituim datele problemei în această formulă, considerăm răspunsul numeric.
Răspuns: 15 N.
Dacă ți-a plăcut sarcina și soluția, atunci poți să o împărți cu prietenii tăi cu aceste butoane.