Dacă luăm două funcții cum ar fi 1) y = √x și 2) y = x 2 pentru x ≥ 0, atunci descrierea proprietăților lor va coincide, în ciuda faptului că graficul lor diferă. Iată programele lor:
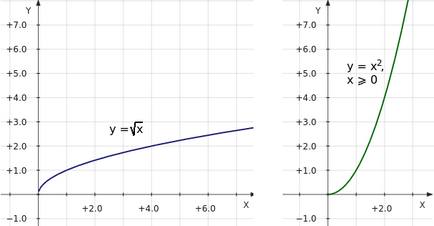
Ambele funcții au același domeniu de definiție [0; + ∞], ambele crescând (x crește cu y), continuu etc.
Dacă nu vedeți graficele acestor funcții, atunci se dovedește că acestea sunt aceleași. Totuși, acest lucru nu este cazul. Prin urmare, matematicienii au introdus o caracteristică suplimentară a funcțiilor - convexitatea lor.
Dacă te uiți la graficul funcției f (x) = √x, poți vedea că este ca și cum ar fi îndoit și spre stânga. Dar graficul f (x) = x2 pentru x ≥ 0 are o convexitate în jos și spre dreapta. Cu toate acestea, va fi suficient să se ia în considerare numai o axă. Luați o poziție verticală și spuneți dacă funcția este convexă în jos sau în sus.
Caracteristica de un fel "ca și cum ar fi îndoit" despre ceea ce nu vorbeste. Trebuie să existe certitudine matematică precisă, care este impusă de convexitatea funcției. Convexitatea graficului este determinată după cum urmează. Prin două puncte arbitrare ale graficului funcției se trasează o linie dreaptă. Dacă complotul parcelei dintre aceste puncte este deasupra liniei trase, atunci spunem că funcția este convex ascendentă. Dacă o parte a graficului dintre puncte se dovedește a fi mai mică decât linia dreaptă prin ele, atunci funcția este convexă în jos.
Deci, funcția y = √x este convexă în sus. Între orice puncte nu trasăm linii, părțile graficului apar întotdeauna deasupra acestor linii:
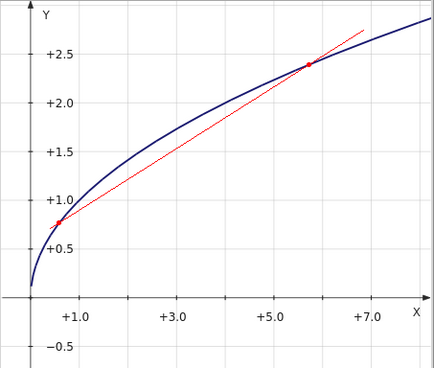
Funcția y = x 2 este convexă în jos, deoarece părțile graficului se dovedesc întotdeauna sub liniile desenate:
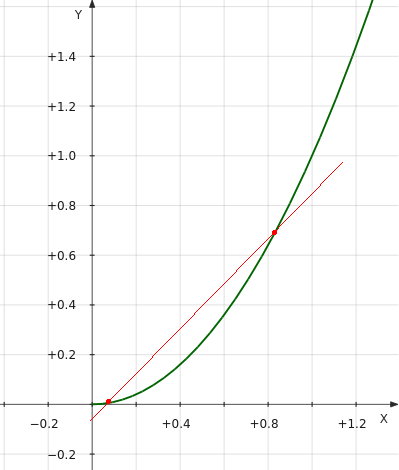
Astfel, atunci când se descriu proprietățile funcțiilor, este de dorit să se specifice convexitatea.