Triunghiul Röhlo are simetrie axială. Ea are trei axe duble de simetrie, fiecare dintre care trece prin vârful triunghiului și mijlocul arcului opus, și o a treia axă de simetrie perpendiculară pe planul triunghiului și extinzându-se prin centrul [* 3]. Prin urmare, grupul de simetrie Rolo triunghi este format din șase hărți (inclusiv identitatea) și coincide cu grupa D 3> simetrii ale unui triunghi echilateral.
Construirea unei busole
Triunghiul Röhlo poate fi construit folosind doar o busolă. nu recurge la un conducător. Această construcție se reduce la succesiunea a trei cercuri egale. Centrul primului selectat arbitrar, al doilea centru poate fi orice punct al primului cerc, iar al treilea centru - fiecare dintre cele două puncte de intersecție a primelor două cercuri.
Proprietăți comune tuturor formelor de lățime constantă
Deoarece triunghiul Röhlo este o figură de lățime constantă, are toate proprietățile comune ale figurilor din această clasă. În special,
- cu fiecare linie de susținere dreaptă, triunghiul Relya are un singur punct comun [14];
- Distanța dintre două puncte ale triunghiului Röhlo de lățime a nu poate depăși [15];
- Segmentul care conectează punctele de tangență a două linii de referință paralele cu triunghiul Röhlo este perpendicular pe aceste linii drepte [16];
- Cel puțin o linie de susținere trece prin orice punct al limitei triunghiului Rielo [17];
- prin fiecare punct P al limitei triunghiului Rielo trece un cerc circular cu o rază a [* 4]. și linia de susținere atinsă spre triunghiul Rielo prin punctul P. este tangentă la acest cerc [18];
- raza unui cerc care are cel puțin trei puncte comune cu limita triunghiului Rölo cu lățimea a. nu depășește [19];
- Teorema Hanfrida Lenz [de] de seturi de lățime constantă Reuleaux triunghi nu pot fi împărțite în două bucăți, diametrul care ar fi mai mică decât lățimea triunghiului [20] [21];
- Relya triunghi, ca orice altă figură de lățime constantă, poate fi înscrisă într-un pătrat [22]. precum și în hexagonul obișnuit [23];
- de constantă lățime teorema Barbier Rolo triunghi perimetrale formulă este valabilă pentru toate cifrele [24] [25] [26].
Proprietăți extreme
Zona cea mai mică
Pentru a găsi zona triunghiului Rölo, putem adăuga aria triunghiului echilateral interior
și zona celor trei segmente circulare identice rămase. susținută de un unghi de 60 °
O figură care are proprietatea extrema opusă este un cerc. Printre toate figurile unei lățimi constante date, aria ei
este maximul [39] [* 5]. Aria triunghiului Rielo corespunzător este mai mică cu ≈10,27%. În aceste limite se află suprafețele tuturor celorlalte figuri cu o anumită lățime constantă.
Cel mai mic unghi
Prin fiecare vârf al triunghiului Röhlo, spre deosebire de celelalte puncte de graniță ale acestuia, nu trece o linie de susținere. ci un set infinit de linii de sprijin. Traversate în partea de sus, ele formează un "pachet". Unghiul dintre liniile extreme ale acestui "pachet" se numește unghiul la vârf. Pentru cifrele cu lățime constantă, unghiul la vârfuri nu poate fi mai mic de 120 °. Singura cifră de lățime constantă care are unghiuri egale cu exact 120 ° este triunghiul Relya [4].
Cea mai mică simetrie centrală
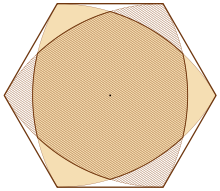
Rolo triunghi (bej) și imaginea sa în conformitate cu simetrie centrală în raport cu centrul său (umbrit). Cele mai multe forma centru simetric, în ea conținea (un hexagon curbilinie), iar cel mai mic centru simetrică, aceasta cuprinde (hexagon regulat) sunt evidențiate printr-o linie groasă
Dintre toate figurile cu lățime constantă, triunghiul Röhlo are cea mai mică simetrie în centru [5] [40] [41] [42] [43]. Există mai multe modalități diferite de a defini gradul de simetrie al unei figuri. Una dintre ele este o măsură a lui Kovner-Besicovich. În cazul general, pentru o cifră convexă C, este egal cu
unde μ este aria figurii și A este figura convexă simetrică centrală a suprafeței maxime conținute în C. Pentru triunghiul Röhlo, o astfel de figură este un hexagon cu laturi curbate, care este intersecția acestui triunghi Röhlo cu imaginea lui la simetria centrală în jurul centrului său [3]. Măsura Kovner-Besicovitch pentru triunghiul Röhlo este
Un alt mod este măsura lui Estermann
unde B este figura simetrică centrală a zonei minime care conține C. Pentru triunghiul Relya, B este hexagonul normal. prin urmare, măsura Estermann este
Pentru figurile simetrice centralizate, măsurile Kovner-Besicovitch și Estermann sunt egale cu una. Dintre figurile cu lățime constantă, doar cercul are simetrie centrală [25]. care (împreună cu triunghiul Röhlo) limitează intervalul de valori posibile ale simetriei lor.
Se rostogolește cu pătrat
Turnarea triunghiului Rielo de către pătrat
Orice figură cu lățime constantă este înscrisă într-un pătrat cu o latură egală cu lățimea figurii, iar direcția laturilor pătratului poate fi aleasă în mod arbitrar [22] [* 6]. Triunghiul Rölo nu face excepție, este inscripționat într-un pătrat și se poate roti în el, atingând în mod constant toate cele patru laturi [44].
Fiecare vârf al unui triunghi, pe măsură ce se rotește, "trece" aproape întregul perimetru al pătratului, deviind din această traiectorie numai în colțuri - acolo vârful descrie arcul elipsei. Centrul acestei elipse este situat în colțul opus al pătratului, iar axele sale mari și minore sunt rotite cu un unghi de 45 ° față de laturile pătratului și sunt egale
unde a este lățimea triunghiului [45]. Fiecare dintre cele patru elipse atinge două laturi adiacente ale pătratului de la distanță
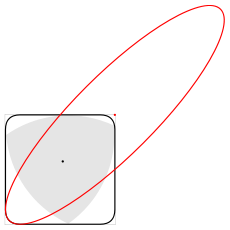
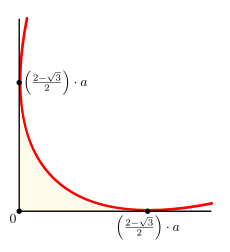
Elipsă (evidențiate în roșu), subliniind unul dintre colțurile figurii (granița sa este evidențiată în negru), care acoperă triunghiul Reuleaux în rotație în pătrat
Unghiul figurinei de rotație. Punctele de tangență ale laturilor unui pătrat cu o elipsă sunt semnate. Galben-deschis arată unghiul pătratului care nu este atins de rotație
Centrul triunghiului Röhlo, pe măsură ce se rotește, se mișcă de-a lungul unei traiectorii compuse din patru arce identice de elipse. Centrele acestor elipse sunt situate la vârfurile pătratului, iar axele sunt rotite cu un unghi de 45 ° față de laturile pătratului și sunt egale
Uneori, pentru mecanismele care realizează în practică o astfel de rotație a unui triunghi, ca o traiectorie centrală, nu alege să lipsească patru arce de elipse, ci un cerc aproape de el [46].
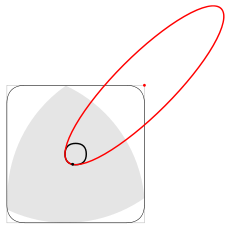
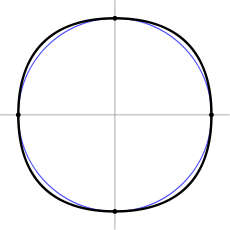
Elipsa (evidențiată în roșu) conturează o a patra curbă de-a lungul căreia se deplasează centrul triunghiului Raelo în timp ce se rotește într-un pătrat
Traiectoria centrului triunghiului Röhlo când se rotește într-un pătrat. Se remarcă punctele de conjugare a patru arce de elipse. Pentru comparație, un cerc este afișat (în albastru) care trece prin aceleași patru puncte
Zona fiecăruia dintre cele patru colțuri necoate este
și, scăzându-le din pătratul pătratului, se poate obține zona figurinei, care formează triunghiul Röhlo în timp ce se rotește în el
Diferența cu pătratul pătratului este ≈1,2%, deci, pe baza triunghiului Rielo, se creează exercițiile. permițând obținerea de găuri aproape pătrate [45].
Forați pătrat în secțiune transversală pe axa frezei
"Am auzit cu toții despre chei. adaptat pentru piulițe cu filet pe stânga, legat într-un nod și apă banane țevile din fontă. Am considerat martisoare astfel de lucruri amuzante, și a refuzat chiar să creadă că ei ne vor întâlni vreodată în viața reală. Și brusc apare o unealtă, permițându-vă să forați găuri pătrate! "
Masina de frezat cu o secțiune transversală sub forma unui triunghi Reuleaux și lame tăietoare, care coincide cu vârfurile sale, produce gaura aproape pătrat. Diferența dintre aceste găuri și pătratul din secțiune este doar în colțurile ușor rotunjite [50]. O altă caracteristică a acestor freze este că ar trebui să nu în timpul axei de rotație pentru a rămâne în vigoare, așa cum este cazul de foraj convenționale în spirală, și descrie în curba secțiunii plane care constă din patru arce de elipse. Prin urmare, cartușul. caracterizat prin aceea că dispozitivul de tăiere este fixat, iar scula de fixare nu trebuie să împiedice această mișcare [45].
Pentru prima dată, Harry Watts, un inginer englez care a lucrat în Statele Unite, a reușit să implementeze o construcție similară a instrumentului. Pentru aceasta, el a folosit o placă de ghidare cu o gaură sub forma unui pătrat în care un burghiu fixat într-un "mandrină plutitoare" se putea mișca radial [50]. Brevetele pentru un cartuș [51] și un burghiu [52] au fost obținute de Watts în 1917. Vânzarea de exerciții noi a fost efectuată de Watts Brothers Tool Works [en] [53] [54]. Un alt brevet SUA pentru o invenție similară a fost emis în 1978 [55].
Motorul Wankel
Schema de funcționare a motorului Wankel
Un alt exemplu de utilizare poate fi găsit în motorul lui Wankel. rotorul acest motor este conceput ca un triunghi Reuleaux [6]. Acesta se rotește în interiorul camerei, suprafața care este format prin epitrohoidă [56]. Arborele rotorului este racordat rigid la roata dințată. care este cuplat la uneltele fixe. Un astfel de rotor cu trei tăișuri se rotește în jurul pinionului, atingând toate vârfurile pereților interiori ai motorului și formând trei regiuni cu volum variabil. fiecare dintre acestea fiind la rândul său o cameră de ardere [6]. Din acest motiv, motorul execută trei cicluri complete de sarcină pe revoluție.
Mecanism de prindere
Mecanismul de clapetă cu came-cam a proiectorului "Luch-2"
O altă aplicație a triunghiului Rölo în mecanică este mecanismul clapetă. realizând mișcarea cadru-cu-cadru a filmului în proiectoarele de film. Graifer proiector „Luch-2“, de exemplu, pe baza Rolo triunghi, care se înscrie într-un cadru pătrat și fixat pe un paralelogram dublu. Rotirea în jurul arborelui de antrenare. Triunghiul mișcă cadrul cu dintele de pe el. Dintele este inclus în perforațiile de film, se trage la cadrul inferior și se întoarce, și apoi ridicându-se la partea de sus a buclei. traiectoria sa este mai aproape de pătrat, mai aproape de vârful triunghiului este ax fix (în mod ideal, o cale pătrat ar permite proiecția cadru ¾ ciclu) [6] [57] [58].
Există o altă construcție a graiferului, bazată și pe triunghiul Raelo. Ca și în primul caz, cadrul acestei apucături efectuează o mișcare cu mișcare alternativă, dar nu este deplasat de unul, ci de două camă ale căror funcționare este sincronizată prin intermediul unei transmisii de viteze [28].
Gloanțe acoperă

Trapă pentru apa recuperată în San Francisco
În formă de triunghi Rölo, se pot realiza capace de găuri - datorită lățimii lor constante, ele nu pot cădea în trapă [59].
În San Francisco. pentru sistemul de recuperare a apei, ecluzele sunt sub formă de triunghi Rölo, dar capacele lor sunt sub formă de triunghiuri echilaterale.
Mecanism cam

Pentru a deplasa obiecte grele pe distanțe scurte, puteți utiliza nu numai structuri pe roți, ci și structuri mai simple, de exemplu, role cilindrice [66]. Pentru a face acest lucru, încărcătura trebuie plasată pe un suport plat montat pe role și apoi împingând-o. Pe măsură ce rolele posterioare sunt eliberate, ele trebuie mutate și așezate în față [67] [66]. Acest mod de transport a umanității a fost folosit înainte de inventarea roții.
În această mișcare, este important ca încărcătura să nu se deplaseze în sus și în jos, deoarece tremuratul va necesita un efort suplimentar de la împingere [67]. Pentru ca mișcarea de-a lungul patinoarului să fie dreaptă. secțiunea lor transversală trebuie să aibă o figura cu lățime constantă [67] [68]. Cel mai adesea secțiunea transversală a fost un cerc. deoarece rulourile erau niște bușteni obișnuiți. Cu toate acestea, secțiunea transversală sub forma triunghiului Rölo nu va fi nici mai rău și va permite obiecte în mișcare atât de simplu [6] [67].
În ciuda faptului că rolele sub formă de triunghi Rølo permit obiecte care se mișcă ușor, această formă nu este potrivită pentru realizarea de roți, deoarece triunghiul Röhlo nu are o axă fixă de rotație [69].
Triunghiul Relo - o formă obișnuită a plectrului (mediator): o placă subțire concepută să joace pe corzile instrumentelor muzicale scoase.
Triunghiul Rölo în artă
arhitectură
Forma triunghiului Rölo este de asemenea folosită în scopuri arhitecturale. Designul celor două arcuri formează un stil gotic caracteristic unui arc ascuțit. dar în întregime se întâmplă destul de rar în structurile gotice [70] [71]. Ferestrele sub forma triunghiului Rölo se găsesc în biserica Fecioarei din Bruges [9]. și de asemenea în biserica scoțiană din Adelaide [71]. Ca element ornamental, apare pe grilele de fereastră ale mănăstirii cisterciene din comuna elvețiană Otriv [70].
Câteva exemple de utilizare



