Există clase semnificative de probleme practice care nu pot fi rezolvate cu ajutorul graficelor luate în considerare. Planul de drumuri și piețe ale orașului este reprezentat cu ajutorul unui grafic plat. Dar dacă această schemă ar trebui utilizată în scopul de a conduce prin oraș, iar traficul pe străzi separate este unul. Apoi săgețile situate direct pe margini pot ajuta.
Se spune că o margine a graficului este orientată dacă unul dintre vârfurile sale este considerat a fi originea, iar celălalt capăt al acestei margini.
Un grafic al cărui margini sunt orientate se numește un grafic orientat.
Marginile unui grafic orientat au un început fix și un final fix și sunt numite arce. Vi Vj ¹ Vj Vi
Semi-gradul de intrare al vârfului unui grafic direcționat este numărul de muchii pentru care acest vârf este un capăt. Denumit de: deg + (V)
Semi-gradul de ieșire a unui vârf al unui grafic orientat este numărul de margini pentru care acest vârf este începutul. Denumit de: deg - (V)
În digraph, traseul este orientat și numit calea.
Nici o margine nu trebuie să se întâlnească de două ori, iar direcția fiecărui arc trebuie să coincidă cu direcția traseului.
O cale este o secvență ordonată de margini ale unui grafic orientat în care capătul muchiei anterioare coincide cu începutul următorului și toate marginile sunt unice.
# 8204; # 8204; # 8204; # 8204; # 8204 ;. # 8204; AD | = 3
Dacă nu puteți "trece" de la un vârf la altul într-un grafic orientat, distanța dintre ele se numește infinită.
Vârful unui grafic orientat se numește sursa. dacă nu intră nici un arc, adică d + (v) = 0.
Un vârf al unui grafic orientat se numește chiuvetă. din ea nu există frunze de arc, adică d- (v) = 0.
Matricea de adiacență este o matrice pătrată de dimensiune n * n, (unde n este numărul de vârfuri ale graficului), care reprezintă în mod unic structura sa.
A =, i, j = 1,2. n și fiecare element al matricei este definit după cum urmează:
aij = 1, dacă ∃ arcul (Vi, Vj),
aij = 0, dacă nu există nici un arc (Vi, Vj).
La intersecția fluxului și coloanei se pune 1 sau 0, în funcție de. Fie că există un arc care merge de la o etichetă a unei linii într-o etichetă a unei coloane.
Liniile matricei de incidență corespund vârfurilor, iar coloanele de margini sau arce.
Matricea de incidență a unui grafic orientat G este o matrice B = (bij) de mărime n × m astfel încât
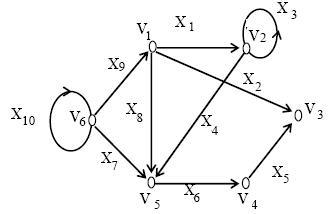
Fie Vi și Vj vârful digraphului G. Vârful Visotimimei de la Vj. dacă există o cale (Vi, y). Orice vârf este atins de la sine. Vitezele Vi și Vj sunt strâns legate între ele dacă sunt realizabile una de alta.
De exemplu, pentru graficul prezentat în Figura 25.2, vârfurile V2 și V3 sunt puternic conectate, vârfurile V1 și V4 sunt puternic conectate, vârful V6 este accesibil din V1. dar punctul V1 nu poate fi atins de V6.
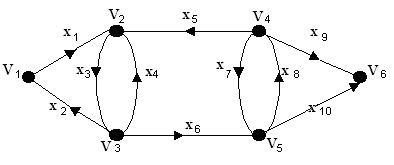
O conexiune puternică a unui grafic G este numit subgraf puternic legat, care nu este un subgraf propriu al oricărui alt subgraf puternic legat de graficul G.
Graficul prezentat în imagine. 25.3 are trei componente puternice de conectivitate. Ele sunt încrucișate cu linii punctate.
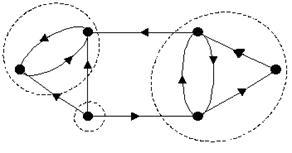
Rețineți că există arce care nu aparțin niciuneia dintre componentele puternice ale conexiunii.
Capacitatea de reinserție într-un grafic este descrisă de matricea de accesibilitate R = [rij], i, j = 1, 2. n, unde n este numărul de vârfuri ale graficului și fiecare element este definit după cum urmează:
rij = 1 dacă vârful xj este atins de la xi,
rij = 0, în caz contrar.
Matricele contrareachabilității Q = [qij], i, j = 1, 2. n, unde n este numărul de noduri ale graficului, este definit după cum urmează:
qij = 1, dacă vertexul xi poate fi atins de la vârful xj,
qij = 0, altfel.
Matricea puternică de conectare a unui grafic orientat D este o matrice pătrată S (D) = [sij] de ordin n. ale căror elemente sunt egale