O funcție logică este o declarație complexă care rezultă din operațiile logice pe simple declarații.
Pentru formarea unor afirmații complexe, operațiile logice de bază sunt cele mai des folosite. exprimată cu ajutorul conectorilor logici "și", "sau", nu ".
De exemplu,
Mulți oameni nu-și plac vremea rea.
Lăsați A = "Mulți oameni preferă vremea rea". Obținem o funcție logică F (A) = nu A.
Bundlele "NU", "AND", "OR" sunt înlocuite de inversarea operațiunilor logice. coroborat. disjuncție. Acestea sunt operațiile logice de bază. cu care puteți scrie orice expresie logică.
O formulă logică (expresie logică) este o formulă care conține doar cantități logice și semne de operații logice. Rezultatul calculării formulei logice este TRUE (1) sau FALSE (0).
Valoarea unei funcții logice depinde de valorile variabilelor sale logice. Prin urmare, valoarea unei funcții logice poate fi determinată folosind o tabelă specială (tabelul de adevăr), care enumeră toate valorile posibile ale variabilelor logice de intrare și valorile corespunzătoare ale funcției.
Operații logice de bază (de bază):
1. Multiplicare logică (conjuncție). din lat. konjunctio - conectați:
• Combinarea a două (sau mai multe) afirmații într-una cu ajutorul sindicatului AND;
• în limbi de programare - și.
• notația: / \. •, și, și.
• În algebra seturilor de conjuncție există o operație de intersecție a seturilor.
O conjuncție este adevărată dacă și numai dacă toate afirmațiile sale sunt adevărate.
exemplu:
Luați în considerare declarația compusă "2 • 2 = 4 și 3 • 3 = 10". Să ne exprimăm simple declarații:
A = "2 • 2 = 4" = 1 (deoarece aceasta este o declarație adevărată)
B = "3 • 3 = 10" = 0 (deoarece aceasta este o declarație falsă)
Prin urmare, funcția logică F (A, B) = A / \ B = 1/0 = 0 (conform tabelului de adevăr), adică această declarație compusă este falsă.
2. Adăugarea logică (disjuncție). din lat. disjunctio - Disting:
• Combinarea a două (sau mai multe) afirmații într-una cu ajutorul uniunii SAU;
• în limbi de programare - Or.
• Desemnarea: \ /, +, sau, sau.
• În algebra seturilor de disjuncții corespunde funcționării unirii seturilor.
Disjuncția este falsă dacă și numai dacă toate declarațiile incluse în ea sunt false.
exemplu:
Luați în considerare declarația compusă "2 • 2 = 4 sau 2 • 2 = 5". Noi propunem simple propoziții:
A = "2 • 2 = 4" = 1 (deoarece aceasta este o declarație adevărată)
B = "2 • 2 = 5" = 0 (deoarece aceasta este o declarație falsă)
Prin urmare, funcția logică F (A, B) = A \ / B = 1 \ / 0 = 1 (conform tabelului de adevăr), adică această afirmație compusă este adevărată.
3. Negație (inversiune). din lat. Inversiune - mă întorc:
• Corespunde unei particule de NOT, combinațiile de cuvinte NU sunt adevărate, CE ESTE sau NU ESTE TRECUTĂ;
• În limbile de programare - Nu;
• Desemnarea: nu A, ¬A, nu
• În algebra seturilor, o completare a unui set universal corespunde negării logice.
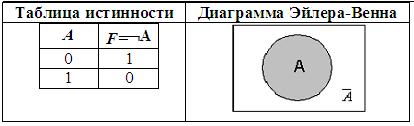
Inversarea unei variabile logice este adevărată dacă variabila însăși este falsă și invers, inversiunea este falsă dacă variabila este adevărată.
¬A = Nu este adevărat că două înmulțite cu două sunt egale cu patru> = 0.
Să luăm în considerare afirmația A. "Luna este un satelit al Pământului"; atunci ¬A va fi formulată după cum urmează: "Luna nu este un satelit al Pământului".
Luați în considerare fraza: "Nu este adevărat că 4 este divizibil cu 3". Indicăm prin A simpla afirmație "4 este divizibil cu 3". Atunci forma logică a negării acestei afirmații are forma ¬A
Prioritatea operațiilor logice:
Operațiile din expresia booleană sunt executate din stânga în dreapta cu paranteze în ordinea următoare.
1. inversiune;
2. Conjuncție;
3. disjuncție;
Parentheses sunt folosite pentru a schimba ordinea specificată a operațiilor logice.
Expresiile logice compuse ale algebrei propoziționale se numesc formule.
Adevărat sau fals, sensul formulării poate fi determinat de legile algebrei logice, fără a se referi la semnificația:
F = (0 \ / 1) / \ (¬0 \ / ¬1) = (0 \ / 1) / \ (1 \ / 0) = 1/1 1 =
F = (¬0 / \ ¬1) \ / (¬1 \ / ¬1) = (1 / \ 0) \ / (0 \ / 0) = 0 \ / 0 =