Matlab. OPTIMIZAREA, PROGRAMAREA LINEARĂ.
Căutați extrema unei funcții a unei variabile. Căutarea unui minim local (într-un anumit interval) este efectuată de funcția [x, y] = fminbnd (FunctionName, IntervalsLength). Dacă este necesar să se găsească un minim local, atunci funcția examinată este luată cu un alt semn și este căutată pentru minimul său, care este de fapt maximul său. În acest caz, valoarea funcției la maxim este valoarea găsită împreună cu celălalt semn.
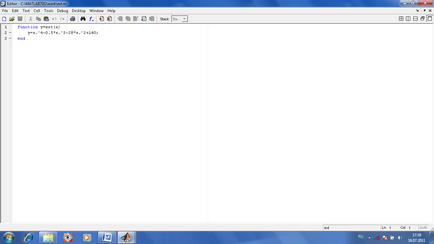
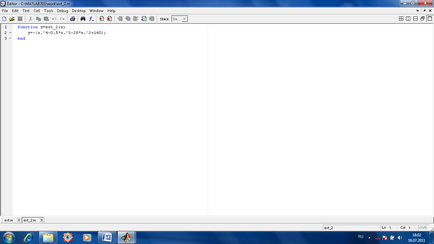
Căutați extrema unei funcții a mai multor variabile. Dacă funcția este calculată pe mai multe variabile, apoi pentru a găsi este utilizată valoarea minimă (după estimarea aproximativă inițiale aproximații variabile în minimul asumat) comanda [x, y] = fminsearch (functionname, vektorNachalnyhPriblizheniyPeremennyh).
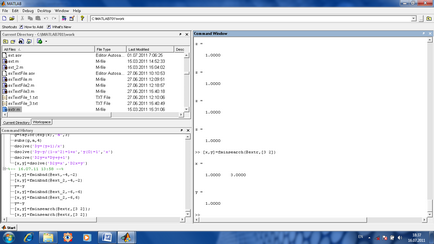
Rezolvarea problemelor de programare liniară. În problemele programării liniare este necesar să se găsească valoarea maximă sau minimă a unei funcții liniare a mai multor variabile cu constrângeri lineare sub formă de egalități sau inegalități. Luați în considerare, de exemplu, o astfel de problemă.
Lăsați funcția L (x1, x2, x3, x4) = x1 + x2 + x3 + x4 și găsiți maximul și valorile variabilelor corespunzătoare maximului său.
Să presupunem că există constrângeri sub formă de inegalități. x1 ≥0, x2 ≥0, x3 ≥0, x4 ≥0.
Să presupunem, de asemenea, că există restricții sub formă de inegalități.
Pentru a rezolva problema de programare liniară (găsirea minimului) vom folosi funcția [x, L, f] = linprog (c, A, b, A1, b1, Lx, Rx)
x vector al valorilor variabilelor, primite ca răspuns; L este valoarea funcției la minim;
(dacă este zero, atunci soluția este suspendată după atingerea numărului maxim de iterații, dacă este pozitivă atunci totul este normal, dacă nu se găsește soluția atunci);
c funcția țintă reprezentată ca vector al coeficienților (în cazul nostru [1 1 1 -1], dar din moment ce avem nevoie de un maxim și funcția [x, L, f] = linprog (c, A, b, A1, Rx) caută un minim, apoi schimbăm semnul în expresia funcției, deci vectorul coeficientului va fi [-1 -1 -1 1]);
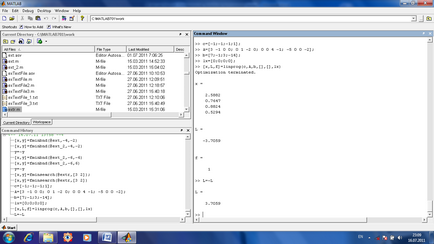
A, constrângeri de sistem b definit într-o formă de matrice Ax≤b (în problema noastră este limitare -x2 3x1 ≤7, x2 -2x3 ≤-1, 4x3 -x4 ≤3, 5x1 + 2x4 ≥14, dar de 5x1 + 2x4 ≥14 nu sunt adecvate, este necesar să se schimbe semnul inegalității în acest caz se va -5x1 -2x4 ≤-14, în acest caz, matricea constă din coeficienți (cu variabile) în aceste inegalități, și coloana b este compus din dreapta (care nu conține variabile ) părți ale inegalităților;
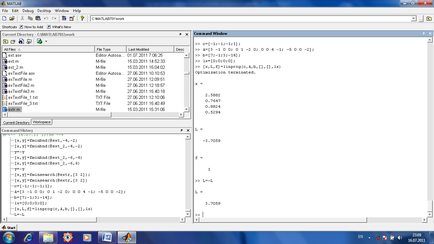
A1, b1 sistemul de ecuații de forma A1x = b (în problema noastră nu există un astfel de sistem de limitări, dar ar putea fi);
Lx, Rx se referă la constrângerile în forma Lx≤x≤Rx, Lx≤x, x≤Rx (în problema noastră există restricții ale formulei Lx≤x, prin urmare vectorul Lx va fi 0 0 0 0).
Atunci când se utilizează funcția linprog, parantezele pătrate goale sunt plasate în lista de argumente în locul celor care nu sunt specificate.
Luați în considerare un alt exemplu de instruire. Fie W = x1 + x2 + 3x3-x4 să fie dat și să se găsească maxim. Să presupunem că există constrângeri sub formă de inegalități.
Am rezolva problema cu funcția [x, L, f] = linprog (c, A, b, A1, B1, Lx, Rx). Pentru ao folosi, trebuie să pregătim argumentele funcției. Vectorul cu coeficienții funcției este egală cu (1, 1 3 -1), ci ca o funcție de cel puțin linprog căutarea și avem nevoie de un maxim, apoi modificați semnul coeficienților funcției și apoi vectorul este (-1 -1 -3 1). matricea A este compusă din coeficienții variabilelor din sistemul inegalităților x1 + 4x3 -5x2 ≤5, x1 -2x2 -3x3 ≤4, x1 + 6x2 + 5x3 ≤4, x2 + ≤1 x3. Deoarece toți au semnul ≤, atunci nu este necesar să se schimbe nimic. Vectorul b constă din laturile drepte ale acelorași inegalități. Matricea A1 din sistemul A1x = b1 nu este relevantă pentru noi (nu există astfel de condiții). Lx, Rx se referă la restricții în formă de Lx≤x≤Rx, Lx≤x, x≤Rx. Avem limitări sub formă de inegalități. x1 ≥0, x2 ≥0, x3 ≥0, x4 ≥0. Apoi vectorul Lx = [0; 0; 0; 0]. În ceea ce privește celelalte tipuri de restricții, deoarece nu avem astfel de restricții, pentru noi ele nu sunt importante.
Probleme de programare neliniară. Problema neliniară diferă de cea liniară. Este un sistem de inegalități liniare Ax≤b, sistemul de ecuații liniare A1x = b1, sistem lx≤x≤rx tipuri de restricții, lx≤x, x≤rx. Cu toate acestea, în afară de acestea familiare (de programare liniară) condiții, există un sistem de tip neliniar de g1 (x) ≤0 constrângeri și ecuații neliniare g2 (x) = 0. Pentru a rezolva problema de programare neliniare (după vectorul de selectare x0 aproximare inițială) este utilizată funcția [x, y, f] = fmincon (F, x0, A, b, A1, B1, Lx, Rx, G), unde G este o funcționalitate M care calculează partea stângă a neliniar constrângeri g1 (x) ≤0, g2 (x) = 0. Dacă unele argumente nu sunt definite, paranteze pătrate sunt plasate în locul lor în apelul pentru funcții.
De exemplu, luați în considerare următoarea problemă. lăsați funcția x1 2 + x2 2 = 1 cu condiția ca x1 x2 = 4, x1 ≥0, x2 ≥0. Vectorul aproximărilor inițiale este considerat a fi x0 = (0,1, 0,1).