Această lege, numită legea gravitației universale, este scrisă în formă matematică după cum urmează:
unde m1 și m2 - greutatea corporală, R - distanța dintre ele (a se vedea figura 11a ..) și G - constanta gravitațională egală 6,67.10-11 Nm 2 / kg 2.
Legea gravitației a fost formulată pentru prima dată de către Newton când a încercat să explice una dintre legile lui Kepler, susținând că pentru toate planetele raportul dintre cubul distanta R de la Soare la pătratul perioadei T de circulație în jurul ei în același mod, și anume,
Vom deduce legea gravitației universale așa cum a făcut Newton, considerând că planetele se mișcă în cercuri. Apoi, în conformitate cu a doua lege a lui Newton la masa planetei MPL se deplasează cu raza R a cercului cu o viteză v și v2 accelerație centripetă / R are o forță F, îndreptată spre Soare (vezi figura 11b ..) Și este egal cu:
Viteza v a planetei poate fi exprimată în funcție de raza R a orbitei și perioada de revoluție T:
Înlocuind (11.4) în (11.3), obținem următoarea expresie pentru F:
Din Legea lui Kepler (11.2) rezultă că T2 = const.R3. În consecință, (11.5) poate fi transformată în:
Astfel, Soarele atrage planeta cu o forță direct proporțională cu masa planetei și invers proporțională cu pătratul distanței dintre ele. Formula (11.6) este foarte asemănătoare cu (11.1), doar masa soarelui în numărătorul fracțiunii din dreapta lipsește. Cu toate acestea, în cazul în care forța de atracție între soare și planeta depinde de masa planetei, această forță va depinde, de asemenea, pe masa soarelui, și, prin urmare, constanta in partea dreapta (11.6) cuprinde o matrice solare ca fiind unul dintre factorii. De aceea, Newton și-a avansat faimoasa presupunere că forța gravitațională ar trebui să depindă de produsul maselor de corpuri și legea a devenit aceeași cu cea pe care am scris-o în (11.1).
Legea atracției universale și legea a treia a lui Newton nu sunt contradictorii. Conform formulei (11.1), forța cu care corpul 1 atrage corpul 2 este egală cu forța cu care corpul 2 trage corpul 1.
Pentru corpurile de dimensiuni obișnuite, forțele gravitaționale sunt foarte mici. Deci, două autoturisme de lângă autoturisme sunt atrase unul de celălalt, cu o forță egală cu greutatea unei picături de ploaie. De atunci, după cum G. Cavendish în 1798 a determinat valoarea constantei gravitaționale, cu formula (11.1) a ajutat pentru a face o mulțime de descoperiri în „lumea de mase uriașe și distanțe.“ De exemplu, cunoscând valoarea accelerației gravitaționale (g = 9,8 m / s2) și raza Pământului (R = 6,4.106 m), este posibil să se calculeze masa MH urmează. Pe fiecare m1 masa corporală în apropierea suprafeței Pământului (adică la o distanță R de la centrul său) forța gravitațională acționează sale atracție M1G egale, în care substituția (11,1) în locul F dă:
din care rezultă că mS = 6.1024 kg.
Întrebări pentru repetare:
· Formulează legea gravitației universale?
Ce este o constantă gravitațională?
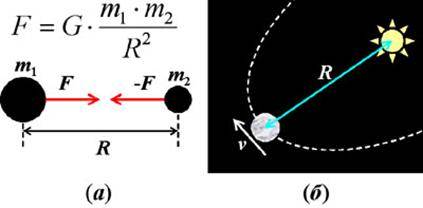
Fig. 11. (a) - la formularea legii gravitației universale; (b) la încheierea legii gravitației universale din legea lui Kepler.
§ 12. PUTEREA DE GRAVITATE. GREUTATE. Imponderabilitate. PRIMUL SPEED SPACE.