O suprafață este suprafața de frontieră formată de deplasarea unui generator rectiliniu de-a lungul unui ghidaj rupt. Suprafețele de granit pot fi împărțite în două tipuri: piramidal și prismatic-
O parte din spațiu, mărginită de toate părțile de o suprafață, este numită corp.
Un poliedron este un corp mărginit de poligoane plane. Considerarea polyhedra este limitată la examinarea prismelor și a piramidelor.
O prismă este un polidron cu aceleași fețe paralele reciproce - baze și fețe laterale - paralelograme. Dacă marginile fețelor laterale sunt perpendiculare pe bază, atunci prisma este numită linie dreaptă. Pentru a specifica o prismă, este suficient să specificați una dintre bazele sale și o margine laterală.
Piramida este un polyhedron, în care o față este un poligon arbitrar care este luat ca bază, iar celelalte fețe (latură) sunt triunghiuri cu un vârf comun, numit vârful piramidei.
Secțiunea de policedru cu un avion. În secțiunea suprafeței de suprafață -
planuri, poligoane, ale căror noduri sunt definite ca punctele de intersecție a marginilor suprafețelor frontale cu un plan secant.
Poligonul unei secțiuni poate fi găsit în două moduri:
- vârfurile poligonului se găsesc ca puncte de intersecție a muchiilor drepte (marginile) cu un plan secant;
- laturile poligonului sunt ambele linii de intersecție a planelor (fețelor) ale polyedrului cu planul secant.
De exemplu, construim secțiunea transversală a prismei de către planul Q proeminent în față (figura 1.80).
Planul secant este perpendicular pe planul frontal al proeminențelor, prin urmare toate liniile situate în acest plan, inclusiv forma transversală pe proeminența frontală, vor coincide cu linia frontală Q v
planul Q. Astfel, proiecția frontală a secțiunii figura 1/2/3 / este determinată atunci când proeminențele frontale ale marginilor prismei cu urmă Qv se intersectează. Proiecția orizontală a figurii secțiunii coincide cu proiecția orizontală a prismei. Proiecția profilului formei secțiunii este găsită de accesoriile proeminențelor punctelor 1,2,3 corespunzătoare marginilor prismei. Dacă presupunem că planul Q se desprinde din partea de sus a prismei, atunci figura secțiunii este pornită
Planul profilului este vizibil, iar dacă nu, linia 2 // 3 // este afișată invizibilă.
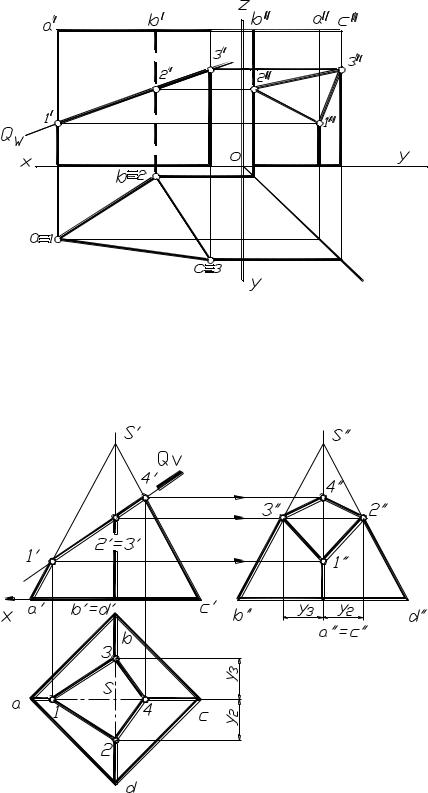
Prism cu gâtul. Ca un exemplu de construcție a unei secțiuni dintr-un polyhedron cu mai multe planuri, luați în considerare construcția unei prisme cu o tăietură formată dintr-o prismă triunghiulară.
În proiecția frontală, marchează proiecțiile punctelor de întâlnire ale marginii B a prismei date cu fețele prismului de decupare: 3 / și 8 /. și punctele de intersecție a marginilor prismei de tăiere cu fețele corpului dat: 1/2/4/5/6/7 /. Noi găsim orizontul -
dal proiecții ale punctelor marcate. Toți se află pe proiecția orizontală a prismei date. Din cele două proiecții obținute de puncte găsim proiecțiile lor de profil. Având în vedere vizibilitatea, conectăm punctele care aparțin fețelor corespunzătoare ale prismei date. În fața AB. punctele 3, 2, 8, în fața BC: punctele 3,5,7,8 și în fața AC. 1,4,6,1.
Piramida cu decolteu. Figura 1.83 prezintă construcția unei piramide cu o decupare (ca urmare a secțiunii piramidei prin mai multe planuri care se proiectează, formând o decupare prismatică). Noi desemnează punctele de proiecție frontală care aparțin simultan unei piramide și prismatice date. Dacă punctele aparțin marginilor unei piramide date, găsim proiecțiile lor orizontale și de profil. Punctele (3) ale intersecției marginii tăieturii prismatice cu fețele piramidei date pot fi găsite în două moduri. Prima metodă constă în trasarea punctelor planului de tăiere S paralele cu baza (ale cărei urme sunt notate în desenul complex). În secțiunea piramidei acest avion
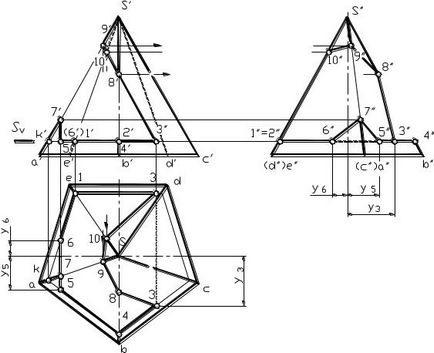
se formează un triunghi asemănător cu baza care trece prin punctul K. Acest punct face parte din punctele 3,1,6,7,5,4,3. De asemenea, puteți găsi puncte pe suprafața piramidei tragând linii drepte prin ele, conectându-le la vârful piramidei și construind în continuare liniile desenate pe planul orizontal al proeminențelor și găsind punctele dorite pe ele. Punctele obținute sunt conectate luând în considerare vizibilitatea în secvența necesară de-a lungul fețelor corespunzătoare ale piramidei date (cele două puncte aparțin unui plan secant și unei fețe a piramidei).
1.18 Organele de rotație
Să luăm în considerare câteva dintre suprafețele revoluției.
Suprafețele formate prin rotirea unei linii drepte. Pentru așa ceva
un cilindru și un con sunt purtate.
Cilindrul de rotație este o suprafață obținută prin rotirea unei linii drepte pe o axă paralelă și limitată de două planuri reciproc paralele.
Conul de rotație este o suprafață formată prin rotirea unei linii drepte (generatrix) în jurul unei axe care se intersectează cu ea (un ghidaj).
Un exemplu de suprafețe formate prin rotirea unui cerc în jurul unei axe fixe este sfera.
O sferă este o suprafață obținută prin rotirea unui cerc în jurul diametrului său.
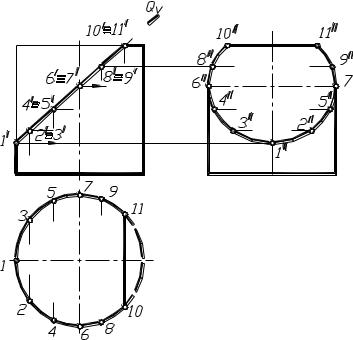
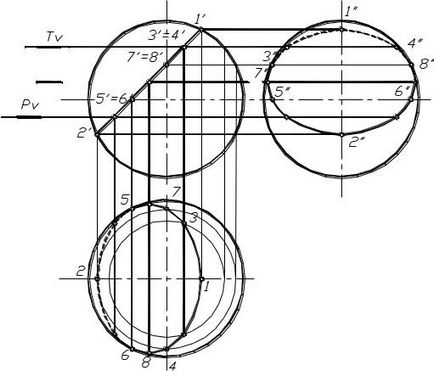
Secțiunea transversală a cilindrului cu un plan. Cu secțiunea transversală a cilindrului,
un plan paralel cu axa de rotație, se obține o pereche de linii drepte (generatoare) în secțiune. Dacă planul secant este perpendicular pe axa de rotație, în secțiune este obținut un cerc. În general, atunci când planul secant este înclinat față de axa de rotație a cilindrului, se obține o elipsă în secțiunea transversală.
Figura 1.84 prezintă un exemplu de construire a proeminențelor liniei de secțiune a unui cilindru printr-un plan Q proeminent în față atunci când în secțiune este obținută o elipsă.
Forma de proiecție frontală în secțiune, în acest caz coincide cu planul frontal al căii ferate și orizontală - proiecția unui cilindru cu o suprafață orizontală - cerc. proiecție profil se bazează pe două proiecții disponibile - igrekovye orizontală și măsurarea frontală coordonatele punctelor în raport cu axa cilindrului și așezându-le pe liniile de proiecție punctele de conectare corespunzătoare.
Secțiunea unui con cu un avion. În funcție de poziția planului de tăiere, se pot forma diferite linii, numite liniile secțiunilor conice, în secțiunea conului de rotație.
Dacă planul secant trece prin vârful conului perpendicular pe baza sa, atunci în secțiunea transversală obținem o pereche de linii drepte - generatoare
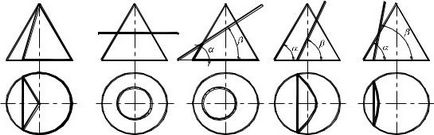
(triunghi - figura 1.85a). Ca urmare a intersecției conului cu un plan perpendicular pe axa conului, se obține un cerc (figura 185b). Dacă planul de tăiere înclinată spre axa de rotație a conului și se extinde în partea superioară, o secțiune conică poate transforma elipsă (planul de tăiere intersectează toate generatoarele conului. - 1.85v Fig). Parabolei este format, în cazul în care planul de tăiere este paralelă cu una dintre generatoarele conului (Fig. 1,85g). Hiperbola este format, în cazul în care planul de tăiere este paralelă cu două generatoare ale conului în funcție de unghiul de înclinare a planului de tăiere la baza conului (Fig. 1.85d).
Se știe că un punct aparține unei suprafețe dacă aparține unei linii a acestei suprafețe. Pentru con, cele mai simple linii sunt generatoare și cercuri. În consecință, dacă prin condiția problemei este necesar să se găsească proiecțiile orizontale ale punctelor care aparțin suprafeței conului, atunci una dintre aceste linii trebuie să fie trasă prin puncte.
Figura 1.86 prezintă un exemplu de construire a proeminențelor unei secțiuni a unui con cu un plan de proiectare frontală, atunci când în secțiune este obținută o elipsă.
Forma secțiunii de pe planul frontal coincide cu traseul planului secant. Notăm punctele caracteristice (a punctelor aparținând conului schița frontală - 1, 6 si 4, 5 - puncte aparținând schița conului profilului) și câteva intermediare (cele mai marcate astfel puncte, mai precis turn secțiunii formei - elipsă). Proiecțiile orizontale și profilate ale punctelor 1,4,5,6 sunt fără construcții suplimentare, deoarece aparțin eseurilor relevante ale conului. Pentru 4 și 5 sunt proiecții ale profilului apartenenței la condițiile de profil schița conului, și apoi măsurarea igrekovuyu coordonate a acestor puncte de axa conului marcat proiecția lor orizontală. Pentru a găsi punctele intermediare ale proeminențelor pot utiliza metoda de tăiere plane paralele cu baza conului sau efectua prin intermediul punctelor reprezentate grafic care formează un con urmat nahozhde-
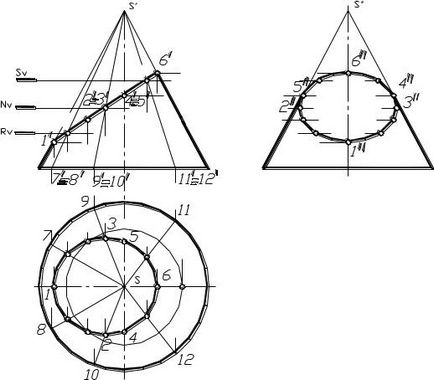
proiecțiile orizontale ale acestor generatoare și găsirea punctelor corespunzătoare pe ele. Apoi, cea de-a treia proiecție a punctelor marcate este construită din cele două proiecții obținute. Proiecțiile obținute de puncte sunt legate printr-o curbă netedă în ceea ce privește vizibilitatea (de exemplu, partea superioară a conului este tăiată de planul Q și, prin urmare, întreaga figura secțiunii pe planul profilului este vizibilă). Dacă o astfel de tăiere nu are loc, atunci pe partea de proiecție a profilului curbei secțiunii 465 va fi reprezentată o linie invizibilă.
Con cu decolteu. Figura 1.87 prezintă un con în care este făcută o crestătură formată din trei planuri cu o anumită poziție care formează o decupare prismatică. Proiecția frontală a figurii secționale coincide cu conturul decupajului prismatic. Pentru a găsi proiecțiile orizontale și de profil ale crestăturii, marchează un număr de puncte necesare. Este necesar să se ia în considerare punctele caracteristice ale eseurilor conului, punctele de inflexiune ale planurilor de decupare și o serie de curbe intermediare pentru acuratețea construcției.
În acest caz, se notează punctele 5.6 și 11.12. Profilul conului; punctele 1, 2, 3, 4, 9, 10, care sunt margini (linii de inflexiune ale planurilor de decupare) ale decupajului prismatic. Pentru o construcție mai precisă a părții parabolice, este necesar să notăm un șir de puncte (ce vor fi ele
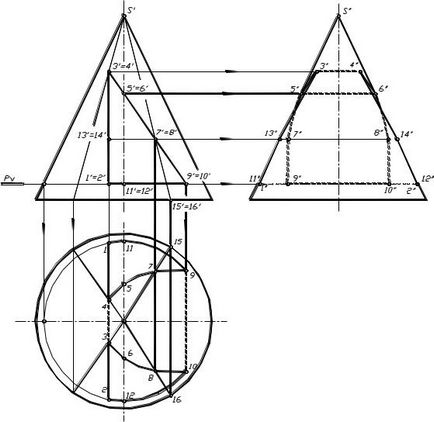
cu cât curba este mai exactă) între 3, 9 și 4, 10 (în acest caz, punctele 7 și 8). Pentru a construi porțiunea decupaj, rezultând partea formată dintr-o hiperbolă, marcat puncte situate între punctele 1 și 3, 2 și 4 (în acest caz, punctul 13 și 14). Ei trebuie, de asemenea, să ia o sumă suficientă.
După construirea proeminențelor orizontale și profilate ale punctelor marcate, proiecțiile decupajului sunt legate de vizibilitate. În plan orizontal, liniile de intrare și ieșire ale decupajului prismatic al conului sunt vizibile. Pe profilul de vizibilitate de proiecție este definit de punctele de frontieră 5, 6 și 11, 12. Linia 5, 7, 9, 11 și 6, 8, 10, 12 la proiecția profil nu este vizibil, dar având în vedere piesele sub formă decupată linie 5 și 7 6, 8 la liniile 3, 13 și 4, 14 vor fi vizibile.
Secțiunea unei sfere de către un avion. Dacă mingea este traversată de un plan, în secțiune se obține întotdeauna un cerc. Acest cerc poate fi proiectat:
- în linie dreaptă dacă planul secant este perpendicular pe planul proeminențelor;
- un cerc cu raza egală cu distanța de la axa de rotație a bilei până schița, în cazul în care avionul se intersectează este paralel cu un plan de proiecție;
- în elipsă. Dacă planul secant nu este paralel cu niciuna dintre planurile de proiecție.
Pentru a construi un punct de proiecție pe suprafața sferei, este necesar să dețină planul de secțiune plan kakoylibo paralel prin el de proiecție și desena un cerc pe care se află acest punct
Figura 1.88 prezintă construcția proeminențelor liniei de secțiune a bilei planului frontal.
Construcția începe cu definirea punctelor caracteristice. Punctele 1 și 2 se află pe schița frontală a mingii (principalul meridian). Aceste puncte sunt capetele axei mici a elipsei, precum și punctele cele mai înalte și cele mai joase. Proiecțiile lor orizontale și de profil se află pe cercurile corespunzătoare ale bilei, pe planurile orizontale și de profil
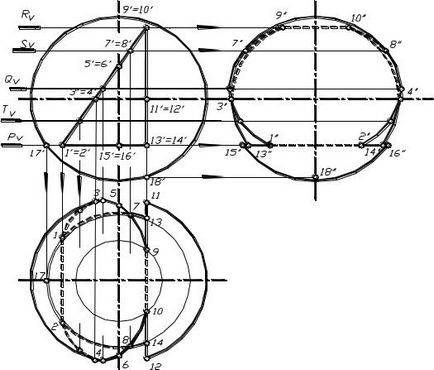
coincid cu axele. Punctele 7 și 8 se află pe profilul mingii (meridianul profilului) și servesc pentru a determina vizibilitatea în planul profilului a proiecțiilor. Proiecțiile orizontale ale acestor puncte sunt situate pe partea frontală și profil. Punctele 5 și 6 se află pe conturul orizontal al mingii (ecuatorul) și servesc la determinarea vizibilității în planul orizontal al proeminențelor. Proiecțiile profilului acestor puncte se găsesc de-a lungul proeminențelor orizontale și frontale. Pentru o construcție corectă a liniei secțiunii, este necesar să găsiți câteva puncte suplimentare. Pentru a le construi, utilizați planuri auxiliare secante (de exemplu planuri orizontale T și P), care în secțiune dau un cerc pe plan orizontal. Punctele obținute sunt conectate printr-o curbă netedă, luând în considerare vizibilitatea acestora.
Un castron cu un gât. Figura 1.89 prezintă construcția proeminențelor unei mingi cu o tăietură formată din trei planuri de o anumită poziție care formează o decupare prismatică.
Pentru a construi proiecțiile crestăturii, marchează punctele necesare. Acestea sunt punctele aparținând eseurilor mingii, punctele de inflexiune ale avioanelor de decupare, precum și o serie de puncte intermediare pentru o construcție mai precisă a liniilor tăiate.