Creșterea finită a formulei Lagrange
Creșterea finită a formulei Lagrange exprimă relația dintre creșterea fiecărui interval continuu pe interval [a; b] și o funcție y = f (x) care poate fi diferențiată pe intervalul (a; b) și valoarea derivatului său: unde c este un număr din intervalul (a; b) Sensul geometric formula Lagrange este după cum urmează: arcul generat această funcție care unește punctele (a, f (a)) și (b; f (b)), există un punct (a, f (c)) (și, eventual, mai multe) , în care tangenta la graficul funcției este paralelă cu coarda care conectează capetele arcului, vezi Fig.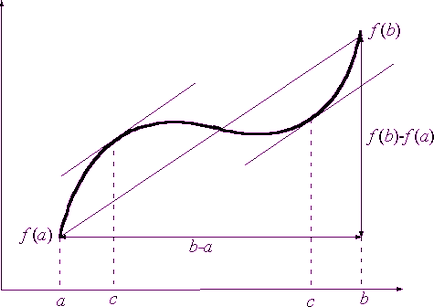
Adesea, formula Lagrange este scrisă într-o altă formă echivalentă: unde Θ este un număr necunoscut care depinde, în general, de x0 și de Δx și satisface inegalitățile 0<Θ <1.
Formula Lagrange pentru o functie a mai multor variabile este urmatoarea: unde 0<Θ <1.
Cu ajutorul formulei Lagrange putem demonstra urmatoarea generalizare: Teorema Cauchy despre valoarea medie: daca functiile f si g sunt continue in intervalul [a; b] și sunt diferențiate pe intervalul (a; b), unde g '(x) ≠ 0 pe (a; b), apoi pe intervalul (a; b) există un punct c. că, la rândul său, această teoremă ușurează dovedirea uneia dintre relațiile importante ale teoriei limitelor - regula de spitalizare.