De obicei oglinzi (plane sau sferice) pentru sisteme optice sunt realizate din sticlă, pe care suprafața este depus prin evaporare în vid, sau prin stratul de metal chimic (argint, aluminiu, cupru), dând reflectanță ridicată (# 961;) luminii, adică, # 1;
Pe lângă această metodă, este utilizată o metodă de fabricare a acestora dintr-o singură bucată de metal, de exemplu aluminiu. astfel de reflectoare mari pot fi folosite în scopuri de astronomie, în sistemele de lumină reflectoarelor.
Luați în considerare fenomenul de reflectare a luminii de la o oglindă sferică. Toate raționamentele sunt efectuate pentru razele care sunt ușor îndepărtate de la axa optică a oglinzii. Astfel de raze se numesc paraxiale. În acest caz, din cauza mici unghiurile de înclinare ale razelor de lumină la axa optică și normala la suprafața de reflexie pot fi înlocuite cu valori ale tangentelor acestor valori și unghiuri sinusale ale unghiurilor înșiși (într-o măsură radială).
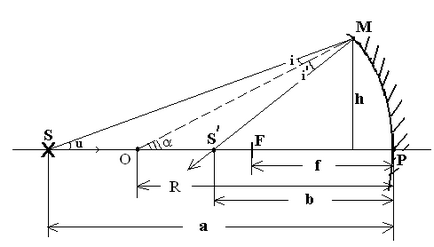
Figura 1 o rază de lumină dintr-un punct de sursă S, situată pe axa optică OR, cade pe suprafața unei oglinzi concave într-un punct M la unghiul i la normal și reflectată de acesta la un unghi i / (i = i /). Normală la suprafață la punctul M este raza R, trase din centrul curburii O la punctul oglinzii M. reflectată fasciculului în punctul M intersectează axa optică în punctul S /. La rândul său, raza SP care se deplasează de-a lungul axei optice se va reflecta în punctul P, care este vârful oglinzii, și va călători înapoi de-a lungul axei optice. În consecință, punctul S / este imaginea punctului S.
Notația introdusă în figura 1 are următoarea semnificație:
a = SP este distanța de la partea superioară a oglinzii la sursa de lumină;
c = S / P este distanța de la partea de sus a oglinzii la imaginea sursei;
R = OM = OP este raza de curbură a oglinzii (normală la suprafața sa);
f = F P este distanța focală;
h este distanța dintre punctul M și axa optică.
Din triunghiurile SMO și OMS / putem scrie:
Adăugând (4) și (5), obținem:
Pentru unghiurile u, u / u # 945; (din cauza dimensiunii lor) pot fi scrise:
Înlocuind valorile acestor unghiuri în formula (6), obținem:
Dacă o → ∞, atunci θ =. Punctul F în care se obține imaginea este în acest caz numit focalizarea principală a oglinzii. Distanța f de la punctul F până la vârful oglinzii P se numește lungime focală și
Inversitatea lungimii focale se numește forța optică a unei oglinzi sferice
Din (5) și (6) avem asta
și anume forța optică a oglinzii sferice depinde numai de raza de curbură a oglinzii sferice.
Din formulele (4) și (5) obținem:
Sensul fizic al formulei (8):
la o poziție strict specificată a obiectului - poziția imaginii este determinată fără ambiguitate.
Determinați lungimea focală a oglinzii sferice concave cu ajutorul unei banchete optice.
Pentru a face acest lucru: i) asamblați unitatea conform figurii 2
O oglindă sferică,
Obiect cu 2 elemente strălucitoare (tensiune pe lampa 6B)
3 ecran mat.
2) Mutarea unui obiect sau a unui ecran mat de-a lungul ghidajului, obțineți o imagine mărită a obiectului. Măsurați de trei ori la distanțe diferite între oglindă și obiect. Folosind o riglă și un pătrat, măsurați în aceste cazuri distanța de la obiect la oglindă și de la oglindă la imagine. Folosind formula (5) pentru o oglindă sferică, determinați lungimea focală.
Înregistrați datele din Tabelul 2.