Școala № 11 din Zhlobin
Tema mea # 13; munca de cercetare științifică "Crearea unui mini-joc" Magic Square ". Sunt # 13; a fost interesat de ideea creării unui mini-joc matematic. Am # 13; cunoașterea limbajului de programare Pascal # 13; nu era suficientă, doar pentru că nu permite crearea de programe # 13; cu o interfață atractivă și ușor de utilizat. M-am confruntat cu două probleme: 1) metode # 13; umplerea matricei pătrate; 2) alegerea limbajului de programare pentru implementarea # 13; jocuri. Prima problemă a fost rezolvată cu ușurință după studierea literaturii relevante. De-a lungul a doua a trebuit să lucreze. A fost aleasă limbajul de programare Delphi, al cărui nucleu este Pascal. Literatura specială a fost studiată, # 13; Forumurile de internet privind unele aspecte au ajutat.
Lucrarea este relevantă pentru cei # 13; care ar dori să înceapă să stăpânească limba de programare Delphi. Înțelepciunea populară spune: "Nu este nimic ce nu puteți # 13; învățați, dar totul poate fi învățat ". Pe exemplul creării unui mini-joc "Magic # 13; pătrat "puteți învăța să utilizați componente, să decorați procedurile, să schimbați numărul 13; proprietățile obiectelor, evenimentele de proces. Un fel de cunoștințe practice - cel mai bun # 13; un fel de cunoaștere eficientă.
Pentru mine personal această lucrare este # 13; un pas important în procesul de învățare și, cel mai important, în aplicarea practică a limbii # 13; programarea la nivel înalt.
Obiectul studiului # 13; este programarea în Delphi.
Subiectul studiului este # 13; dezvoltarea de programe pentru crearea de mini-jocuri în limbajul de programare Delphi.
Scopul studiului nostru # 13; au existat:
teoretic # 13; și dezvoltarea unui program pentru crearea unui mini-joc "Magic Square".
v analizați scopul și # 13; Caracteristici Delphi;
v analizează modalitățile de rezolvare a problemelor # 13; crearea de mini-jocuri în Delphi;
v Dezvoltați un program de mini-jocuri # 13; "Magic Square"
Acest lucru se va asigura
Ø # 13; dezvoltare și # 13; Aplicarea abilităților de programare;
Ø # 13; obținerea abilităților # 13; programarea în sistemul popular de programare Delphi;
Ø # 13; informal # 13; mastering materialele de programare în Delphi.
În conformitate cu scopul și # 13; Ipoteza de cercetare a fost stabilită și rezolvată următoarele sarcini:
Scrieți un program # 13; crearea unui mini-joc "Magic Square", care, în primul rând, generează câmpul # 13; o pătrată magică de 3 × 3 cu niște celule goale; în al doilea rând, # 13; verifică dacă matricea pătrată este un pătrat "magic".
MAGIC SQUARE, masă pătrată de numere întregi, în # 13; care însumează numerele de-a lungul oricărui rând, orice coloană și oricare dintre cele două principale # 13; diagonalele sunt egale cu unul și același număr.
Magic # 13; un pătrat de origine chineză veche. Conform legendei, la data de # 13; domnia Împăratului Yu (aproximativ 2200 î.Hr.) din apele Fluviului Galben (Fluviul Galben) a apărut pe locul 13; țestoasa turcească, pe coaja căreia erau înscrise hieroglife misterioase # 13; (Figura 1, a), iar aceste semne sunt cunoscute ca lo-shu și sunt echivalente cu magia # 13; pătratul prezentat în Fig. 1, b. În secolul al XI-lea. despre patratele magice învățate în # 13; India, iar apoi în Japonia, unde în secolul al XVI-lea. Pătrățele magice au fost dedicate # 13; literatura amplă. Europenii cu piețe magice introduse în secolul 15 din secolul al XV-lea; Scriitorul bizantin E.Moshopoulos. Primul pătrat, inventat de cel european, # 13; este pătratul lui A. Durer (figura 2), ilustrat pe faimoasa sa gravură Melancolie # 13; 1. Data creării gravurii (1514) este indicată de numerele situate în două puncte centrale # 13; celule din linia de jos. Pătratele magice au atribuit diferite mistic # 13; proprietăți. În secolul al XVI-lea. Cornelius Heinrich Agrippa a construit piețele din secolele 3, 4, 5, 6, 13; 7, 8 și 9, care au fost asociate cu astrologia celor șapte planete. Se credea că un pătrat de argint gravat pe argint protejează de la # 13; ciuma. Chiar și astăzi, în rândul atributelor consumatorilor europeni, puteți vedea # 13; magic pătrate.
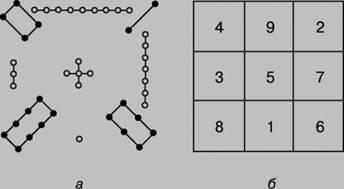
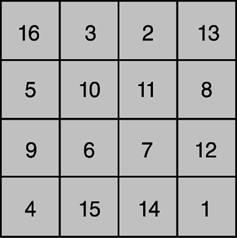
Fig. 2. SQUARE OF DYUR.
În secolele al XIX-lea și al XX-lea # 13; interesul în patratele magice a izbucnit cu vigoarea reînnoită. Au început să exploreze cu # 13; folosind metode de algebră mai mare și calcul operațional.
Fiecare # 13; Elementul pătratului magic este numit celulă. Pătratul a cărui parte # 13; este alcătuită din celule n, conține celule n2 și se numește pătratul n-a # 13; comandă. Cele mai multe pătrate magice utilizează primul n # 13; numere naturale consecutive. Suma numerelor S din fiecare linie, # 13; fiecare coloană și pe orice diagonală, se numește constanta pătratului și este egală cu S = # 13; n (n2 + 1) / 2. Se dovedește că n ≥ 3. Pentru un pătrat de ordinul trei S # 13; = Ordinul 15, al patrulea - S = 34, ordinul 5 - S = 65.
Două # 13; Diagonalele care trec prin centrul pătratului sunt numite diagonalele principale. Linia întreruptă este denumită diagonală, care, ajungând la marginea pătratului, continuă # 13; paralel cu primul segment de pe marginea opusă (o astfel de formă diagonală # 13; celulele umbrite din Figura 3). Celule care sunt simetrice în jurul centrului # 13; pătrat, se numesc oblic-simetric. Astfel, de exemplu, celulele a și b din figura 13; 3.
Fig. 3. LOMA DIAGONALĂ ȘI COSMETICĂ # 13; CELL
Magic # 13; pătratele de ordin ciudat pot fi construite utilizând metoda franceză # 13; geometrul secolului al XVII-lea. A. de la Lubera. Luați în considerare această metodă folosind exemplul pătratului al cincilea # 13; (Figura 4). Numărul 1 este plasat în celula centrală a rândului de sus. Toate # 13; numerele naturale sunt aranjate într-o ordine naturală ciclic de jos în sus în # 13; diagonalele celulelor de la dreapta la stânga. După ce a ajuns la marginea superioară a pătratului (ca în cazul # 13; numărul 1), vom continua să umplem diagonala pornind de la celula de jos # 13; următoarea coloană. După ce ați ajuns la marginea dreaptă a pătratului (numărul 3), continuați # 13; umpleți diagonala care merge de la celula din stânga la rândul de mai sus. Ajungerea la numărul # 13; celule (numărul 5) sau unghi (numărul 15), traiectoria coboară o celulă # 13; în jos, după care procesul de umplere continuă.
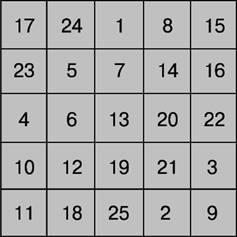
Fig. 4. METODA DE LA LABERA.
Programarea este # 13; procesul de creare (elaborare) a unui program care poate fi depus # 13; secvența următoarelor etape:
1. Specificația # 13; (definirea, formularea cerințelor pentru program).
2. Dezvoltarea algoritmului.
3. Codificare (scrierea algoritmului 13 în limba de programare).