Fie mt să se deplaseze cu viteza de-a lungul unui cerc de rază r în jurul axei fixe de rotație (figura 1.4a). Poziția punctului pe cerc determină vectorul de rază, iar vectorul creșterii sale elementare este îndreptat de-a lungul tangentei către cerc. Noi introducem conceptul unui vector elementar unghiulare: este modulo colț egal rotație elementar d # 966;. direcționat de-a lungul axei de rotație și este asociată cu direcția de rotație a regulii șurubului dreapta, și anume, direcția de rotație a degetului mare trebuie să coincidă cu direcția de rotație a punctului material, apoi direcția de deplasare spre înainte a vectorului definește degetul mare (Figura 1.4a.).
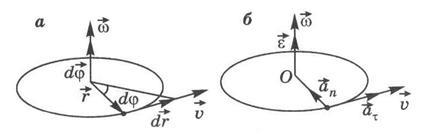
Viteza de rotație mt caracterizează viteza unghiulară egală cu prima derivată a vectorului de deplasare unghiulară în raport cu timpul t:
Direcția vectorului de viteză unghiulară și vectorul deplasării unghiulare elementare coincid.
Viteza de schimbare a vitezei unghiulare este caracterizată de vectorul de accelerare angulară, egal cu primul derivat al vitezei unghiulare în raport cu timpul t:
În plus față de valorile enumerate mai sus, viteza de rotație n este utilizată pentru a descrie mișcarea de rotație a corpului. definită ca numărul de revoluții pe corp per unitate de timp și perioada de revoluție T, ca timp al unei revoluții complete. Următoarea relație este valabilă # 969; n și T:
Se stabilește relația dintre caracteristicile liniare (,) și unghiulare (,) în cazul mișcării de rotație.
Folosind definiția vectorului produs de doi vectori (vezi apendicele 1) și Fig. 1.4a. pot fi scrise
Expresia (1.9) ne permite să obținem următoarele formule pentru relația dintre caracteristicile lineare și unghiulare:
1) pentru vitezele u
2) pentru accelerații ,,