
Maestrul de secretele rezervate!
Ce este Fortune, fericirea tuturor triburilor
Ținut în ghearele lui victorios?
Dante. Comedie divină.
Iadul. VII, 67-69
Folclorul școlar conține o poveste despre un bărbat care, cu ajutorul unui calculator, a dezvoltat un sistem pentru a juca "Sportloto" și a câștigat o avere. Această persoană nu a fost văzută și nu există, deoarece nu există o strategie câștigătoare cunoscută pentru acest joc. Cu alte cuvinte, nu puteți specifica un astfel de mod de a juca, în care suma câștigată va fi întotdeauna mai mare decât banii cheltuiți pentru achiziționarea de carduri. Strategiile pe care le propunem nu fac excepție. Cu toate acestea, cu Sportloto și alte jocuri similare există multe probleme matematice interesante. Vom vorbi despre unele dintre ele.
7 * 10-8; în aceeași notație, p (49,5)
3 * 10 -6 (vă puteți dovedi singuri).
SportPrognoz este jucat după cum urmează. Din calendarul competițiilor sportive sunt alese 13 meciuri, rezultatul cărora, potrivit organizatorilor loteriei, este dificil de prevăzut. Jucătorul trebuie să facă o predicție a rezultatelor acestor meciuri, introducerea în fiecare dintre cele 13 celule din tabel semnul „1“ dacă el crede că echipa gazdă va câștiga, „2“ - echipa vizitatoare și „0“ în cazul unei egalități. După ce rezultatele meciurilor devin cunoscute, se determină cărțile câștigătoare. Bonusurile sunt împărțite între cei care au ghicit cel puțin 11 rezultate și cresc cu o creștere a numărului de predicții corecte din card. Fiecare predicție va fi vectorul 13-dimensional (adică, un șir de 13 numere) cu componente de 0, 1 și 2. De exemplu, vectorul x = (1,1,0,2,2,1,2,0,0, 0,1,1,2) răspunde câștigurilor oaspeților în 4, 5, 7 și 13 meciuri, gazdele - în 1, 2, 6, 11 și 12 meciuri și remize - în cadrul celorlalte întâlniri.
În jocul "Sportloto" trebuie să ghici 6 din 49 sau 5 din 36 de numere. Câștigătorii sunt considerați cărți în care cel puțin 3 dintre numerele trase aleatoriu sunt pierdute. Prognoza în acest caz poate fi descrisă de un vector dimensional 49- (36-) care conține "0" în 43 (31) poziții și "1" în 6 (5) poziții rămase. Numerele de articole unice corespund numerelor previzionate.
În fiecare circulație, un jucător poate oferi mai multe variante ale previziunilor. Noi numim un set de aceste variante un sistem l, dacă există cel puțin unul dintre ele, indiferent de rezultatul circulației, în care cel puțin rezultatele sunt corect ghicite. Pentru noi, numai l-sistemele cu 11<=l<=13 для «Спортпрогноза» и с 3<=l<=6 (5) для «Спортлото». Очевидные примеры l-систем с максимальным l получаются при заполнении всех возможных вариантов прогноза. Эти системы не очень интересны хотя бы потому, что количество заполняемых при этом карточек «Спортпрогноза» равно 1 594 323, т.е. нужно затратить около полумиллиона рублей и около двух лет непрерывной (по полминуты на карточку) работы. Для «Спортлото» соответствующие числа ещё больше. Плохо и то, что, даже справившись с заполнением, нельзя быть уверенным в том, что сумма выигрыша превзойдет сделанные затраты. Для меньших l мы будем стараться придумать такие системы, в которых общее число вариантов было бы как можно меньше.
Deci, dacă joci pe sistem, atunci cel puțin una dintre predicțiile tale va fi în mod necesar destul de adevărată. În acest caz, numărul de carduri achiziționate nu va fi foarte mare.
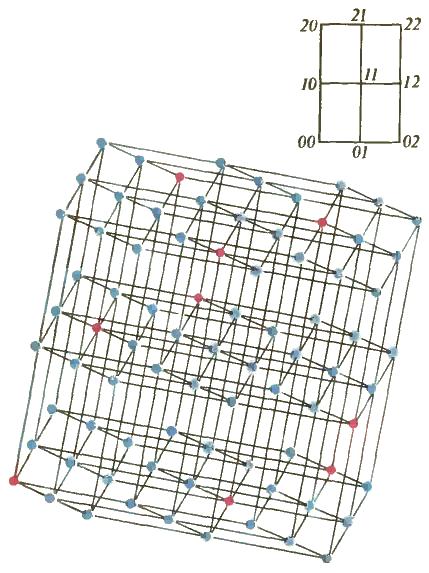
Structura spațiului E 4 3. Figura superioară prezintă 9 puncte din spațiul E 2 3. numerotat de la 0 la 8 în sistemul de numere ternare. Marginile sunt conectate la puncte, numerele "ternare" ale cărora diferă una de cealaltă într-un singur simbol (punctele sunt la o distanță de 1). E 4 3 este obținut din E 2 3 prin înlocuirea fiecărui punct cu 9 puncte din E 2 3; spațiile diferite sunt de asemenea numerotate cu numerele "ternare" de la 0 la 8. Numărăm punctele din fiecare dintre aceste spații în același mod ca în figura superioară. Apoi, numărul "ternar" al fiecărui punct din E 4 3 este obținut prin atribuirea numărului punctului la numărul acelui spațiu E 2 3. în care se află. Figura prezintă nouă puncte aparținând sistemului liniar C0 -.
Previziune sport pentru 4 meciuri
Va fi mai ușor să explicăm ideea construirii de sisteme l folosind exemplul jocului din SportPrognoz-4, care propune să ghicească rezultatele a numai patru meciuri. Denumim setul tuturor vectorilor tridimensionali ai trei simboluri - zerouri, unul și două - de către E 4 3. Dimensiunea sistemului 4 este apoi egală cu numărul de elemente ale setului E 4 3 (= 81). Cazul sistemului 3 vă face să vă gândiți deja. Problema noastră reduce la alegerea din E 4 3 un subset C al numărului minim de vectori astfel încât pentru orice vector e ∈ E 3 în C se poate specifica cel puțin un vector c care diferă de e în cel mult o poziție.
Definiția. Distanța Hamming între vectorii a și b este numărul de componente distincte ale acestor vectori.
De exemplu, distanța dintre vectorii a = (0,1,2,0) și b = (0,2,0,0) este egală cu d (a, b) = 2.
Exercițiul 1. Verificați dacă distanța Hamming satisface inegalitatea triunghiului
Luați în considerare următorul sistem C0. (0,0,0,0); (1, 1, 1, 1); (2,0,2,2); (0,1, 1,2); (0,2,2,1); (1,1,2,0); (2,1,0,1); (1,2,0,2); (2.2, 2.0).
Să demonstrăm că Co este un sistem 3. Verificarea directă arată că distanța între orice pereche de vectori C0 este 3. inegalitatea triunghiului la Hamming distanță există vectorul e € E 3. 4 la o distanță de 1 simultan de doi vectori a și b C0 (altfel d (a, b) = 2). Setul de vectori din E 4 3. localizat la o distanță de 4 3 total 81 vector! Prin urmare, orice vector din E 4 3 aparține unuia dintre astfel de seturi, care urma să fie dovedit.
Exemplul 1. Un vector (2, 1, 2, 1) aparține setului de vectori localizați la o distanță 4 3 situată la o distanță de n. localizat la o distanta j Cn i * (q-1) i a vectorilor (Cn i este coeficientul binomial, egal cu n / / (n-i)!
8 (Limita Hamming). Dovedește asta pentru orice cod
k<=Logq [q n /V(n,t)]
([x] este partea intreg a lui x). (3)
Dacă egalitatea este valabilă pentru parametrii de cod în (3), atunci codul este numit perfect.
Teoria matematică a codării, care a apărut cu aproximativ patruzeci de ani în urmă, este acum o știință dezvoltată și foarte profundă. La izvoare au stat Claude Shannon, deja menționați Richard Hamming, Marcel Golay și alți oameni de știință. Pentru mai multe informații despre codurile, corectarea erorilor, puteți citi în cărțile Arsinova MN Sadowski LE „Coduri și matematică“ (Moscova, „Știința“, 1983, Biblioteca „Quantum“, vol. 30), A. Yaglom M. Yagloma, IM "Probabilitate și Informații" (M. Nauka, 1973).
Este ușor de văzut că sistemele l-perfecte coincid cu codurile perfecte. În special, sistemul 3 pentru jocul mini-SportPrognoz este un cod cu q = 3, k = 2 și n = 4, corectând o eroare. Din cele de mai sus, rezultă că acest cod este liniar (în sensul Exercițiului 2) și este perfect și conține, așa cum ar trebui, q k = 9 vectori.
Sistemul propus 3 pentru o serie de patru meciuri permite generalizarea a 13 meciuri în cazul "real"; acest lucru are ca rezultat un sistem de 12 care cuprinde 3 10 = 59049 carduri. Presupunem că vectorul x ∈ E3 13 aparține sistemului C1. dacă coordonatele sale satisfac următoarele ecuații (din nou în modulul 3):
Ca mai sus, numărul unui vector va fi setul primelor nouă coordonate.
Exercițiul 9. Fie numărul vectorului x = (x1, X13) € C1 fiind (x1, X10) = (0,1,1,1,2,0,2,1,2,1). Găsiți x.
Aprobarea. Sistemul 12 construit este liniar și perfect.
Într-adevăr, permiteți vectorilor x și y să satisfacă (4), atunci ambele x + y și 2x satisfac acest sistem de ecuații. Este ceva mai dificil să se demonstreze că distanța dintre oricare doi vectori ai lui C1 este de cel puțin trei. Luați în considerare 2 vectori x, y ∈ C1. Dacă numerele lor sunt aceleași, atunci x = y. Dacă numerele diferă în trei sau mai multe poziții, atunci totul este dovedit. Fie ca numerele să difere într-o poziție, să zicem, i-lea. Apoi remarcăm că orice xi (1<=i<=10) входит с ненулевыми коэффициентами в правые части по меньшей мере двух уравнений системы (4), т. е. по меньшей мере две из трёх последних координат векторов x и y будут различными. Если же номера векторов x и y различаются в двух позициях, скажем, i-й и j-к, то для доказательства достаточно показать, что они различаются ещё по крайней мере в одной позиции. Этого может не быть только в случае, когда i-я и j-я переменные в правые части всех уравнений (4) входят с одинаковыми коэффициентами. Проверка показывает, что таких переменных не существует. Итак, доказано, что расстояние между двумя любыми векторами x, y€C1 не меньше трёх. Тогда множества векторов из E3 13. находящихся от x и y на расстоянии <=1, не пересекаются. В соответствии с упражнением 7 каждое такое множество содержит 27 = 3 3 векторов. Общее же количество векторов в системе равно числу различных номеров, т. е. 3 10. а общий объём соответствующих им непересекающихся множеств равен 3 10 *3 3 =3 13. что совпадает с числом всех возможных карточек. Что и требовалось доказать.
Sistemul 12 construit este un cod cu q = 3, n = 13, k = 10, care corectează o eroare. Acest cod reprezintă un reprezentant al familiei de coduri Hamming perfecte cu q = 3, n = (3 m -1) / 2, k = n-m.
Să revenim puțin timp la sistemul C0 pentru mini Sport Prognoza. Noi scriem toți cei nouă vectori în rândurile mesei. Prin ștergerea din această tabelă a oricărei coloane, obținem un sistem liniar de nouă vectori pentru SportPrognoz-3. Se poate demonstra că acest sistem este cel mai bun dintre cele liniare, adică conține cel mai mic număr posibil de carduri. Se pare că respingerea condiției de linearitate face posibilă îmbunătățirea acestui sistem. Cel mai bun 2-sistem neliniar de lungime 3 constă doar din cinci vectori. Aici este:
* - Se știe că este imposibil să se îmbunătățească.
Un remarcabil 9-sistem de lungime 11
Cu o observație apropiată a mesei, un asterisc clipește singur în mijlocul acestuia. Aici este un remarcabil 9-sistem C2 de lungime 11. Istoria și aplicațiile sale ar putea servi drept poveste pentru un roman matematic fascinant. Dar mai întâi câteva cuvinte despre eroina. Acesta este un sistem perfect liniar. Perfecțiunea este ușor de dovedit dacă știm că oricare doi vectori ai sistemului se află la o distanță de cel puțin cinci. Apoi, ca și mai înainte, seturile (729 = 3 6) ale vectorilor din E3 11 situate la distanță <=2 от некоторой точки системы, не пересекаются. Поскольку в каждом из этих множеств 243=3 5 векторов, суммарный объём этих множеств совпадает с общим числом векторов в E3 11 .
Dăm ecuațiile care conectează numărul ternar (x1 .x2.X6) al oricărui vector x care aparține sistemului C2. cu celelalte cinci coordonate:
În plus față de acest sistem ternar M. Golay în lucrarea sa, în 1949, a descris un alt sistem liniar perfectă - sistem de 20-C3 lungime 23 vectori de zerouri și cele - codul cu parametrii q = 2, n = 23, k = 12, 3 fix eroare. Acest sistem conține 2 12 = 4096 vectori și ar putea fi util pentru "Sport Forecast" pentru 23 duel într-un joc fără remiză.
Exercitarea 11. Folosind rezultatele Exercițiilor 7 și 8, arată că sistemul C3 este perfect (și prin urmare conține cel mai mic număr posibil de carduri între sistemele cu astfel de parametri).
Descoperirea făcută de Virtacallio, cu atât mai surprinzător este faptul că pentru q = 3 alte l-sisteme perfect non-triviale cu l<=n-2 ни для каких значений n не существует. При l=n-1 существуют еще системы с параметрами, приведёнными в конце предыдущего параграфа. При q=2 список нетривиальных совершенных систем с l<=n-1 исчерпывается 20-системой C3 и семейством (n-1)-систем с n=2 m -1 и k=n-m. Эти два утверждения следуют из глубокой теоремы о совершенных кодах, доказанной только в начале 70-х гг.
Problemele matematice care apar în legătură cu codurile Goleigh C2 și C3, de regulă, sunt destul de dificile. Chiar și problema găsirii rapide (nerecuperabile) a cărții câștigătoare a sistemului C2 în funcție de rezultatul cunoscut al circulației este foarte dificilă. Cei care doresc să-și încerce mâna la această problemă dificilă (deși rezolvată) ar trebui să folosească sistemul de ecuații (5) și să acționeze în spiritul exercițiilor 6 și 9. Poate că veți putea să deschideți un nou mod de a rezolva această problemă?
Această din urmă problemă, ne dorim aici să atingeți din cauza „Sportprognoz“ are loc atunci când un jucător presupune că t a n meciuri disponibile oricare dintre cele trei rezultate - o remiză, castiga si a pierde una dintre echipe, și b = nt meciuri câștigurile sale sunt aproape de necrezut. (De exemplu, într-un meci de fotbal „Barcelona“ (Madrid) - „Star“ (Perm), o echipa ar putea cel mai bine să se bazeze pe tragere.) Notăm E2,3 (b, t) o multitudine de vectori de lungime b + t, în care mai întâi coordonate b iau valorile 0 sau 1, iar ultimul t - 0, 1 sau 2. C sistem-l mixt "Sportprognoz" constă din vectorii E2,3 (b, t), că pentru orice vector de € E2,3 (b, t) există un vector c ∈ C care se află la o distanță Hamming de cel mult l.
12. Arătați-le de la distanță <=l от фиксированного вектора a€E2,3 (b, t) находится SUMi=0 l 2 l-i Cb i Ct l-i векторов.
13. Construiți un sistem 3 la t, b = 2, format din șase cărți.
Este deja clar că construcția sistemelor de jocuri „Sportloto“ implică luarea în considerare a unei multitudini de vectori ai pluralitatea n E2, w vectori binari de lungime n care conțin unități exact w. Nu știm niciun sistem bun pentru Sportloto, dar puteți obține o inegalitate simplă care să arate că un astfel de sistem ar trebui să conțină câteva cărți. Numarul lor, desigur,
depinde de cât de înalte cerințele noastre pentru câștigul așteptat. Ca mai sus, să numim o mulțime de cărți m-sistem D, dacă la orice rezultat al rundei, cel puțin una dintre aceste cărți va câștiga cel puțin m numere. Luați în considerare "Sportloto - 6 din 49". 6-sistem D0 conține C49 6 = 13983816 carduri - toate vectorii din setul E2 49.6 vectori binari de lungime 49 cu șase unități. În orice sistem D1-5 există două c1 și c2 vector cu d (c1, c2) = 2. De fapt, oricare doi vectori care conțin același număr de unități sunt unul de celălalt la o distanță uniformă. Prin urmare, dacă nu există vectori c1 și c2 astfel încât d (c1, c2) = 2, apoi minc1, d c2 (c1, c2) = 4, și există un vector y € E2 49,6. care este cel mai apropiat de sistemul este un vector de y la o distanță de 2. Apoi, dacă y este rezultatul circulației, în D1 nu se va găsi o carte cu cinci numere castigatoare.
Exercițiul 14 (limita Hamming pentru vectorii cu același număr de vectori).
a) Dovada ca numarul de vectori in E2 este 49.6. situate la distanță <=2s от данного вектора c€E2 49,6. равно
M (s) = SUMi = 0 s C6 i C43 i = SUMi = 6-s 6 C6 i C43 6-i
b) Dovada ca | D1 | este numarul de carti din sistemul S1 - nu mai putin de [C49 6 / M (1)] = 53992
([x] este cel mai mic număr întreg mai mare sau egal cu x).
În mod similar, se arată că orice 4-sistem D2 nu poate conține mai puțin de 1014 carduri, orice D6 sistem - mai puțin de 54 de carduri. Pentru "Sportloto - 5 din 36" | D1 |> = 2417, | D2 |> = 79, | D6 |> = 8.
În concluzie, oferim un exemplu de 2-sistem D pentru un mini Sportloto, în care este necesar să ghicești 6 din 8 numere:
Deoarece orice rezultat al cursei y conține două zerouri, există un vector C € D astfel încât în unele coordonate vectorii y și c ambele să conțină zero. Atunci distanța dintre y și c nu este mai mare de două; D este într-adevăr un sistem 2. Arătăm că nu există 2 sisteme cu un număr mai mic de vectori. Într-adevăr, trei vectori împreună conțin doar șase zerouri, și chiar dacă sunt toți în poziții diferite, există încă două poziții care nu conțin zerouri. Prin punerea zeroului vectorului y pe aceste poziții, vedem că acesta se află la o distanță de 4 de la fiecare dintre cele trei vectori ai sistemului. Prin urmare, un sistem D de lungime 8 este optim.
Candidat de Științe Tehnice A. BARG,
Candidat de Științe Tehnice S. LITSYN