în cazul în care
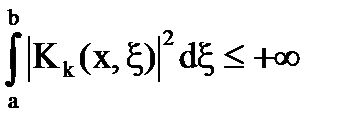
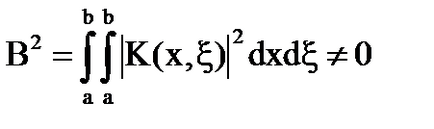
este determinată de formula:
Deoarece seria din (19) converge uniform, putem schimba ordinea sumării și integrării:
Denumim seria Neumann. (23)
Această funcție este numită rezolvarea ecuației (1). Soluția ecuației poate fi scrisă:
Dacă solul este calculat, atunci soluția ecuației poate fi scrisă imediat ().
Definiție: Noi spunem că ecuația integrală (1) are rezoluție R (x, # 958, # 955;), în cazul în care soluția ecuației poate fi scrisă ca (24), iar această soluție este unică pentru orice termen liber f (x).
Este evident că dacă ecuația integrală are un resolvent, atunci este unică.
Într-adevăr, să fie. ecuația are doi resolvenți și. Apoi soluția unică a ecuației poate fi scrisă sub forma:
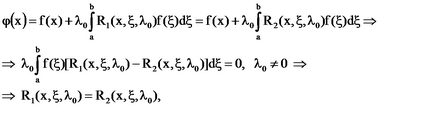
deoarece f (# 958;) este o funcție arbitrară.
Notă: Rezolvatorul a fost definit numai pentru valori # 955; astfel încât. Cu toate acestea, resolventul există în întregul plan al variabilei complexe # 955, cu excepția unor valori izolate # 955;
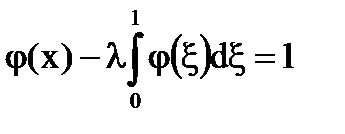
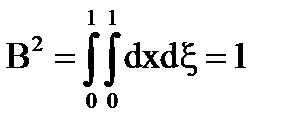
Seria Neumann converge pentru | # 955; |<1.
în special cu # 955; ≠ 1 (în interiorul și în exteriorul cercului # 955; | = 1; pe cerc, exceptând numai # 955; = 1).
Observație: Pentru unele ecuații Fredholm seria (23) converge pentru toți # 955;
Să presupunem asta
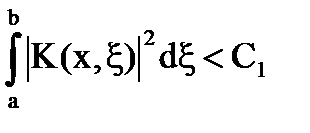
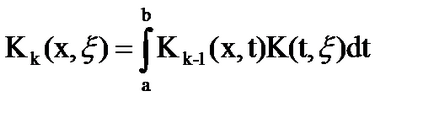
Prin inegalitatea Cauchy-Bunyakovskii:
Integrarea prin # 958 ;, obținem
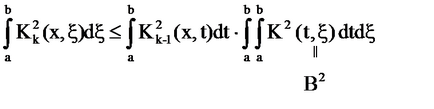
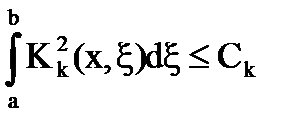
Aici. care este
Prin urmare, seria converge pentru.
Rezoluția îndeplinește următoarea ecuație integrală:
Acest integru este numit trasatura "k" a nucleului sau urmei nucleului "k" iteratat. Avem pentru x = # 958;
După integrarea peste x în raport cu [a, b]:
Un exemplu. Construiți rezolvatorul ecuației integrate cu ajutorul unor kerneluri iterate.
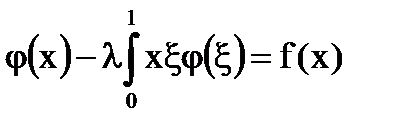
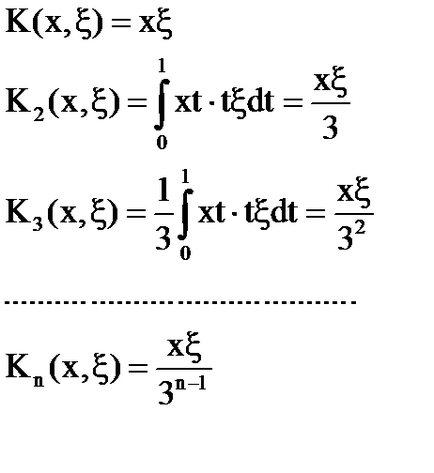
Soluția ecuației integrale:
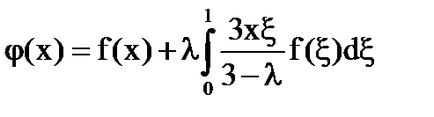
Sarcina pentru munca independenta:
Găsiți nucleele iterate pentru kernelurile indicate pentru a și b
și să construiască solvenții.
Construcția resolventului pentru următoarele kerneluri