Determinarea constantelor de integrare se face pe dl zaklyuchitel etapă a calculului procesului de tranziție, atunci când au fost deja găsite celelalte componente ale soluției-TION. Constantele de integrare sunt determinate prin înlocuirea condițiilor inițiale corespunzătoare în soluție cu funcția dorită.
Fie soluția pentru funcția dorită i (t) să conțină doar o singură constantă de integrare:
Constanta de integrare se găsește înlocuind în soluție condiția inițială pentru funcția în sine, adică i (0):
.
Să presupunem că soluția pentru funcția dorită i (t) conține două integrații constante și are forma:
Constantele integrării în acest caz se găsesc prin substituirea în soluție a condițiilor inițiale pentru funcția i (0) în sine și pentru primul său derivat:
Ca urmare a soluției comune a acestui sistem de ecuații, se determină constantele de integrare A1 și A2 necesare.
Secvența de realizare a etapelor individuale de calcul al proceselor tranzitorii prin metoda clasică este prezentată mai jos sub forma unei diagrame.

Note: 1. Efectuarea tuturor etapelor indicate în diagramă de către celule este obligatorie și necesară.
2. Primii cinci pași din rândul superior al diagramei pot fi executați în orice ordine, deoarece nu depind unul de altul.
Un exemplu. Pentru circuitul din Fig. 132 elemente cu parametri presetate: E = 100 V, R = 50 ohmi, R1 = 20 Ohms, R2 = 30 Ohm, C = 83,5 uF determina i1 curent după-punere în comutație.
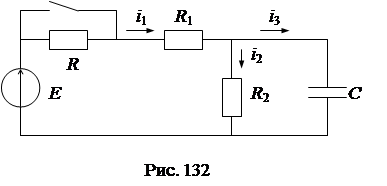
1) Forma generală a soluției pentru funcția cerută:
2) Determinarea constituentului staționar al circuitului după comutare:
3) Ecuația caracteristică și rădăcina ei:
4) Condiția inițială independentă uc (0) de la calculul circuitului înainte de comutare:
5) Sistemul de ecuații diferențiale în conformitate cu legile lui Kirchhoff pentru circuit după comutare:
6) Condiția inițială i1 (0), necesară pentru determinarea constantei de integrare din ecuația (1):
7) Determinarea constantei de integrare:
8) Soluția pentru funcția dorită:
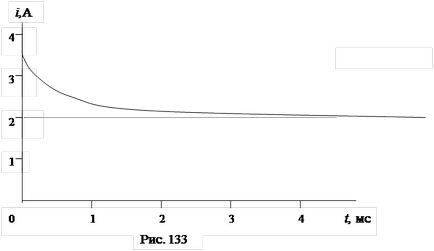
9) Diagrama grafică a funcției căutate i1 (t) este prezentată în Fig. 133:
9. Metoda operatorului pentru calculul tranzitorilor
Dacă sistemul de ecuații diferențiale care descrie procesul tranzitoriu în schemă este rezolvat prin metoda operațională, atunci metoda de calcul a procesului tranzitoriu este de asemenea numită operațională sau asemănătoare operatorului.
Metoda operatorului SINTEZĂ constă în faptul că, în prima etapă efect ing funcției de timp i (t), u (t), denumit originalele sunt înlocuite de noi funcții neko torymi I (p), U (p), numit operator de IMAGINEA -niyami. Corespondența dintre funcția originală f (t) și operatorul IMAGE zheniem-F sale (p) se stabilește pe baza unei conversia directă a integralei La Place:
unde Û - semn de conformitate; p = s + jw este operatorul complex Laplace.
Dacă s # 61472; = 0, apoi p = jw. și transformarea Laplace devine o transformare Fourier, care stă la baza metodei complexe de calcul al circuitelor de curent alternativ.
Transformarea Laplace ne permite să înlocuim operațiunile de tipul al doilea cu funcțiile funcțiilor (diferențiere și integrare) asupra operațiilor de primul tip (multiplicare și diviziune) asupra imaginilor operatorului acestor funcții.
Calculul proceselor tranzitorii prin metoda operatorului se efectuează în mod convențional în 3 etape.
La prima etapă a sistemului de calcul al ecuațiilor diferențiale este compus Nye conform legilor Kirchhoff la funcțiile originale, după aplicarea transformării Laplace-transformă în sistemul de ecuații algebrice pentru imagini cu valori de operă ale acestor funcții.
În a doua etapă, se rezolvă sistemul ecuațiilor operatorului algebric cu privire la funcția necunoscută, rezultând expresia funcției dorite în formularul operator F (p).
La etapa a 3 final se realizează o tranziție inversă din soluția operator TION găsită pentru funcția necunoscută F (p) pentru funcția corespunzătoare de timp f (t), r. F. Deplaseaza între funcția de imagine F (p) f inițială ( t).
Teoretic, tranziția inversă de la imaginea operatorului funcției F (p) la f (t) inițial este stabilită pe baza transformării inverse Laplace:
.
În practică, pentru tranziția inversă se utilizează metode mai simple și mai convenabile, și anume formula de descompunere și tabelul de corespondență.