Să luăm în considerare mișcarea constantă a unui lichid carbonat care are loc într-un mediu poros, când depozitul este dezvoltat la presiunea rezervorului sub presiunea de saturație. În acest caz, gazul dizolvat este eliberat din ulei și două faze se mișcă: ulei și gaz liber. Teoria mișcării unui lichid carbonat a fost dezvoltată mult mai devreme decât teoria lui Buckley-Leverett. Primele studii hidrodinamice privind mișcarea unui lichid carbonat într-un mediu poros aparțin LS Leibenzon, iar primele experimente privind determinarea permeabilităților de fază pentru lichide și gaze au fost realizate de Wycombe și Botset în 1936.
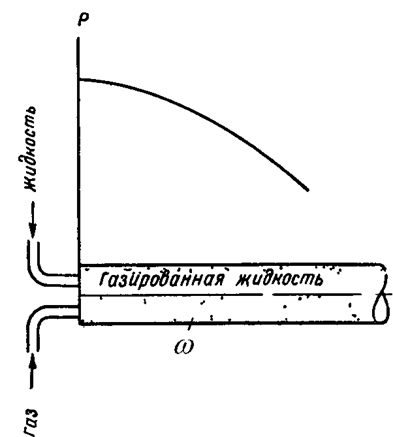
Să considerăm mișcarea staționară rectilinie a unui lichid carbonat într-un mediu poros care umple o conductă de secțiune constantă w (figura 70). Se presupune că filtrarea fiecărei faze respectă legea lui Darcy, adică
unde mzh. mr sunt, respectiv, viscozitatea lichidului și a gazului, care se presupune a fi constante (adică, independent de presiunea P);
relativă permeabilități de fază pentru lichid și, respectiv, gaz;
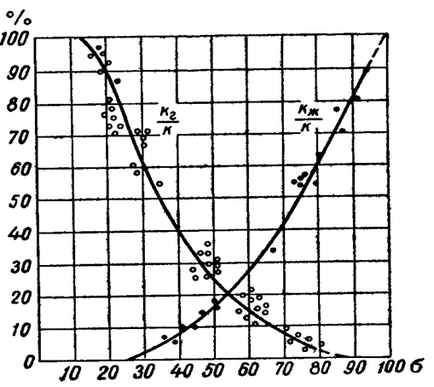
Natura curbelor permeabilităților relative ale fazelor. obținută experimental, este prezentată în Fig.
Caracteristicile caracteristice ale curbelor sunt notate:
1) cu o cantitate mică de permeabilitate a gazului (saturație ridicată cu lichid) <1, т.е. незначительное количество свободного газа весьма сильно уменьшает проницаемость жидкости . и, следовательно, дебит жидкости Qж. Поэтому стараются не допускать чрезмерного выделения газа на забоях скважин, чтобы не снизить фазовую проницаемость жидкости ;
2) dimpotrivă, lichidul este mult mai puțin capabil să miște gazul decât gazul lichid; pentru mici s. și anume la saturație scăzută, lichidul scade foarte puțin.
Să găsim cantitatea totală de gaz (liberă și dizolvată) și să aducem această cantitate volumetrică de gaz la presiunea atmosferică.
Debitul de lichid Qj conține volumul de gaz dizolvat Qgp. care după reducerea la presiunea atmosferică poate fi exprimată prin ecuația:
unde d este coeficientul de solubilitate al gazului în lichid.
- greutatea gazului care se dizolvă într-un volum unitar de lichid atunci când presiunea este mărită cu 1 atm;
- greutatea gazului dizolvat;
P este presiunea absolută.
Gasim viteza gazului liber, redus la presiunea atmosferica. Pe baza lui (10.29).
Apoi debitul volumetric total al gazului (QG) la capul puțului la o scădere a presiunii la valoarea șobolanului atmosferic va fi determinat de suma:
sau luând în considerare (10.31) și (10.32):
Definiți factorul de gaz Г, care este raportul debitului de gaz, redus la condițiile atmosferice, la rata de lichid, adică
Introducem următoarea notație:
Integrăm (10.44) și (10.45), obținem:
- Funcția fără dimensiuni (10.47)
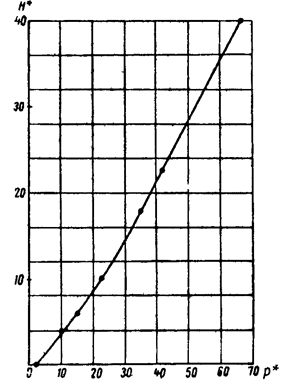
Dependența este reprezentată grafic (graficul 74) prin integrarea grafică utilizând ecuația (10.47). Această dependență a fost construită pentru prima dată de B.B. Lapukom și are forma prezentată în Fig. 75.
Astfel, putem folosi toate formulele pentru mișcarea unui fluid incompresibil omogen, în care presiunea P trebuie înlocuită cu funcția lui Khristianovich N.
Folosind funcția Khristianovich (10.46), se poate scrie, de exemplu, expresia pentru debitul de lichid QZH dintr-o sondă situată în centrul unei formațiuni circulare folosind formula Dupuy:
Funcția H va fi distribuită în același mod ca presiunea în filtrarea unui fluid incompresibil omogen: pentru o mișcare plană-radială, conform legii unei curbe logaritmice, pentru o mișcare paralelă rectilinie, liniar.
Secvența calculelor prin funcția Khristianovich este următoarea: cunoașterea presiunilor conturului PC-ului. RK și factorul de gaz F se găsesc prin și din formula (10.39), și apoi și din grafic (Fig. Cunoscând și din ecuația (10.46) găsim HC și HK. după care toate elementele mișcării sunt fără dificultate.
Tehnica de calcul destul de laborioasă obținută în acest mod poate fi considerabil simplificată dacă se ține cont de faptul că într-un interval larg dependența conform graficului (figura 75) este reprezentată de o linie aproape dreaptă. Prin urmare, cu o precizie suficientă, putem lua:
unde A și B sunt constante.
Luând în considerare (10.48), obținem:
sau. având în vedere (10.43), avem:
Valoarea coeficientului unghiular A din formula (10.48), determinată din grafic (figura 75), este egală cu.
Astfel, formula (10.49) arată că, pentru calcule aproximative, lichidul carbonat poate fi considerat ca un fluid incompresibil omogen fictiv care se deplasează într-o formație în care parametrul trebuie înlocuit cu o cantitate.
În dezvoltarea acestei metode, M.M. Glogovsky și M.D. Rosenberg a stabilit că parametrul A într-un domeniu destul de larg este scris în mod satisfăcător de formula:
unde a este determinată de expresia (10.36), presupunând că: