În matematică, există multe exemple de situații care pot exista în realitate, dar nu au o explicație logică și, prin urmare, ne-au pus într-un final complet. Următoarele probleme legate de teoria probabilităților nu vă vor permite să vă plictisiți și să vă ajutați să vă testați abilitățile mentale.

Imaginați-vă că participați la un spectacol în care prezentatorul vă arată trei porți. În spatele uneia dintre ușile se află un premiu - o mașină nouă, iar pentru cele două rămase - două capre. Puteți alege orice ușă și obțineți exact premiul care este ascuns în spatele ei.
Tu alegi ușa, și ducând apoi deschide una dintre celelalte două uși (maestru știe unde mașina este ascunsă, dar deschide ușa întotdeauna, în spatele căreia există o capră).
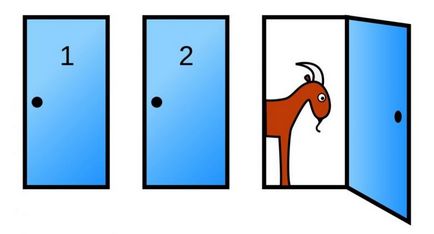
Facilitatorul vă întreabă:
- Vrei să-ți schimbi alegerea? Sau să te oprești la aceeași ușă pe care ai ales-o?
Decizia ta?
Deci, decideți să lăsați opțiunea anterioară.
La urma urmei, nu există nici o diferență dacă să schimbați ușa sau nu. Din moment ce au rămas doar două uși, șansa de a ghici unde este mașina este de 50/50. Corect?

Răspunsul corect este că trebuie să vă schimbați întotdeauna alegerea, deoarece probabilitatea de a câștiga mașina va fi de două ori mai mare.
Un jucator a carui strategie ar fi sa schimbe usa aleasa de fiecare data va juca doar daca alege initial usa din spatele caruia se afla masina. Deoarece probabilitatea de a alege masina cu prima încercare de la unu la trei (sau 33%) șansa de a nu de a alege o mașină, în cazul în care jucătorul se va schimba alegerea sa, este de asemenea egală cu unu la trei (sau 33%). Aceasta înseamnă că jucătorul care a folosit strategia pentru a schimba ușa va câștiga cu o probabilitate de 66% sau două până la trei. Acest lucru va dubla șansele de a câștiga jucătorul, a cărui strategie - de fiecare dată când nu își schimbă alegerea.
Tot nu crezi? Să presupunem că ați ales numărul de ușă 1. Iată toate opțiunile posibile pentru ceea ce s-ar putea întâmpla în acest caz:

Dacă părăsiți alegerea inițială, veți câștiga o dată de la trei; dacă schimbați alegerea - ghiciți de două ori de la trei.
Încă nu esti sigur? Să facem același lucru, doar cu 50 de uși. Alegeți numărul de ușă 1.
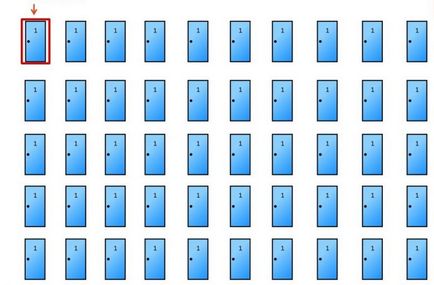
Și deschidem celelalte 48 de uși, în spatele cărora sunt capre ascunse. Încă mai aveți încredere în alegerea dvs.? Amintiți-vă că aveți o șansă din 50 pentru a ghici ușa potrivită la prima încercare. Aici funcționează același principiu.

Răspuns: Șansa ca două persoane în birou să aibă o zi de naștere în aceeași zi este de 50%.
Dacă numărul ajunge la 366, este garantat statistic că cel puțin două persoane vor avea zile de naștere coincide, deoarece sunt posibile doar 365 de zile de naștere probabile. Cu toate acestea, dacă luăm în considerare faptul că toate zilele de naștere sunt la fel de probabil, că, pentru un grup de 57 de oameni probabilitatea unui astfel de coincidență ar fi de 99%.

Cum aflăm?
Să ne întoarcem la cele 23 de colegii de la birou, pentru a înțelege modul în care vozmozhno.Sformuliruem conversa: nu există doi oameni în zilele de meci de grup rozhdeniya.Vyyasnit probabilitatea ca cel puțin două persoane în biroul sarbatorit ziua de nastere in aceeasi zi, este foarte dificil atunci când se confruntă direct cu probabilitate etim.Vyyasnit că nimeni în ziua de naștere grup nu se potrivesc mult mai ușor.
Probabilitatea ca două persoane să nu aibă zile de naștere coincide este:
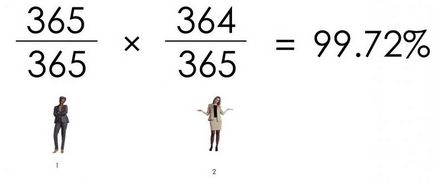
Probabilitatea ca trei persoane să nu aibă zile de naștere coincide este:
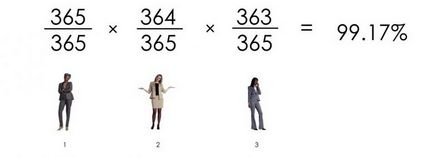
Probabilitatea ca patru persoane să nu aibă zile de naștere coincide este:
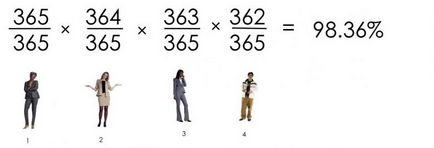
Vedeți la ce ajungem? Probabilitatea ca zilele de naștere să nu coincidă la 23 de persoane este:

Deoarece șansa ca nimeni să nu se fi născut în aceeași zi este de 49,3%, șansa de a coincide cel puțin două persoane este de 50,7%.
Iată cum arată curba de probabilitate:
În acest colectiv, în medie, angajatul are 2,85 prieteni. Cu toate acestea, numărul mediu de prieteni cu care prietenii acestei persoane sunt prieteni este de 3.39.
Acești oameni au fost cei care au un număr mediu de prieteni, după cum se arată mai sus. Prin urmare, ele sunt cele mai populare membri ai colectivului. Dar cel mai important este faptul că 17 din 20 de persoane din birou sunt prieteni ai cel puțin unuia dintre acești oameni:
Un prizonier excitat, pentru că acum probabilitatea de supraviețuire este de 1/2 în loc de 1/3, ca unul dintre prizonieri, A sau C, va pomilovan.Zaklyuchonny Un deținut spune secret C care B va fi executat. Cu prizonierul, de asemenea, entuziasmat, deoarece el încă mai crede că probabilitatea de supraviețuire a unui deținut A este 1/3, iar probabilitatea sa de supraviețuire a crescut la 2/3.
Cine dintre ei se înșeală?
Răspuns: Prizonierul S.
1) Înițial, toți cei trei deținuți au o șansă din trei pentru a fi iertați. Garda a spus că deținutul B va fi executat, ceea ce înseamnă că evenimentele se vor desfășura în conformitate cu unul din cele două scenarii:
- C va fi iertat (1 șansă din 3)
- Și va fi iertat și moneda a arătat "B" (1 șansă din 6)
2) Asta înseamnă: șansele ca deținutul A să fie iertat reprezintă jumătate din șansa de a fi iertați C. Și prizonierul B nu are nici o șansă să fie iertat.
3) Deci, probabilitatea A de a fi grațiată rămâne neschimbată - 1/3, în timp ce probabilitatea C de a fi grațiată crește la 2/3.
Dacă sunteți în continuare îndoieli, aruncați o privire la lista completă a șanselor fiecărui prizonier:
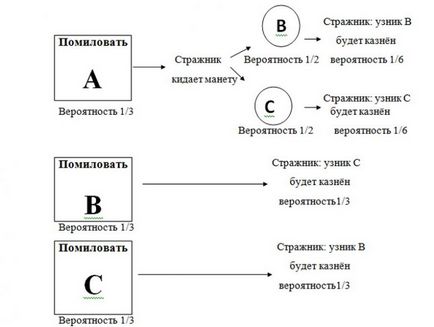
Și dacă te uiți la un exemplu în cazul în care garda a raportat că deținutul va fi executat în, vom vedea că deținutul C are de două ori șansa de a fi grațiat, decât Deținut din:
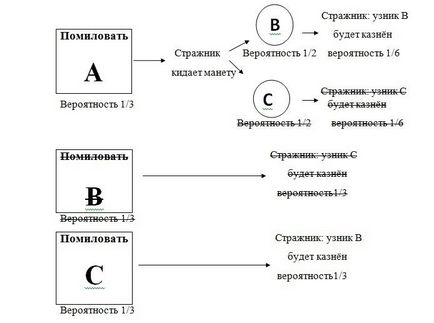
Deci, cum știm sigur că într-o șansă de 0% de a fi iertat, și că C are de doua ori sansa de a fi grațiat, mai degrabă decât A, atunci:
Garda spune că B va fi executat

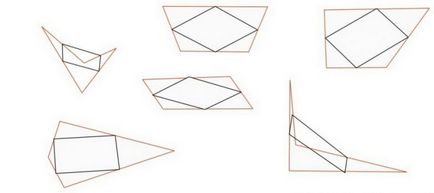
5. Paralela ideală a unui poligon cu patru laturi
Desenați un poligon cu patru laturi.
Poate fi de orice dimensiune, formă neregulată, concavă, convexă etc. Principalul lucru este că are patru colțuri și laturi drepte.
Marcați punctul cu mijlocul de pe fiecare parte a poligonului.
Conectați punctele centrale una la cealaltă. De fiecare dată veți avea un paralelogram ideal.