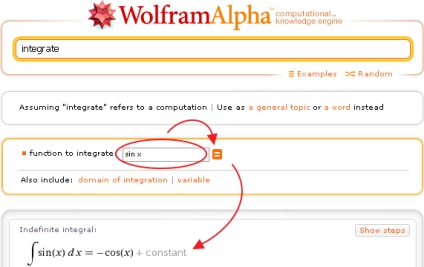
Pentru a integra funcțiile în Wolfram | Alpha, interogarea integrată este utilizată. Puteți utiliza, de asemenea, integral. Uneori Wolfram | Alpha înțelege de asemenea formatul abbreviat int. Cu toate acestea, este mai bine să nu o utilizați, deoarece int este folosit în mod tradițional pentru a face referire la întreaga parte a unui număr.
Iată câteva exemple de funcții de integrare în Wolfram | Alpha.
Pentru început, "cea mai dificilă întrebare":- integrați 1
- integrați x ^ 2-2x + 3

Sfat: pentru a obține o soluție pas-cu-pas, nu uitați de butonul "Afișați pașii".
Următorul integral al unei fracții raționale poate fi o sarcină destul de complexă (a se vedea soluția pas-cu-pas):
- integrat (x ^ 2-3x + 1) / (x ^ 3-8)
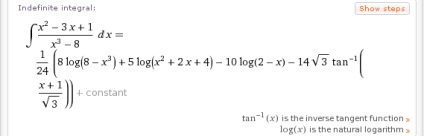
- integral (sinx) ^ 3 (cosx) ^ 4
- integral x ^ 3sinx

- integrat x ^ 2ln (x ^ 3)
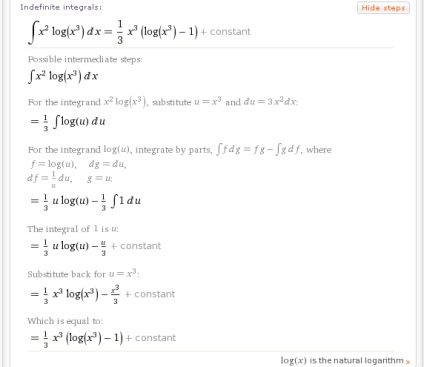
- integra