Operatori de bază: operatori aritmetici, logici și relaționali.
Numărul de operatori matematici în MATLAB destul de mare și include următoarele operații aritmetice:
- divizarea matricelor de la stânga la dreapta (M1 / M2); - divizarea matricelor de la dreapta la stânga (M1 \ M2).
Operatorii relaționali servesc la compararea a două cantități, vectori sau matrici, toți operatorii relaționali au două cantități comparate și sunt scrise în următoarea formă:
Acești operatori efectuează vectori de comparare cu elemente înțelept sau matrici de aceeași mărime și expresia logică este evaluată la 1 (Adevărat), în cazul în care elementele sunt identice, iar valoarea 0 (False) în alt mod.
Operatorii logici servesc la implementarea operațiunilor logice elementale pe elemente ale matricei de aceeași mărime:
O funcție este un obiect unic care realizează anumite transformări ale argumentelor sale și în același timp returnează rezultatele acestor transformări. Funcțiile au, în general, o listă de argumente (parametri) închise în paranteze.
Un set de funcții elementare (toate funcțiile elementare trebuie scrise în programe cu litere mici)
le prezentăm o descriere, iar în funcțiile trigonometrice, unghiurile sunt măsurate în radiani:
- h (modulul) abs (x); - ex (exponent) exp (x); -
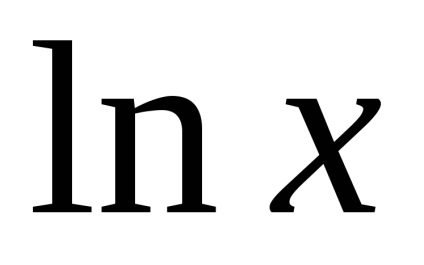
-
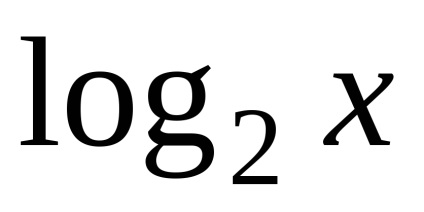
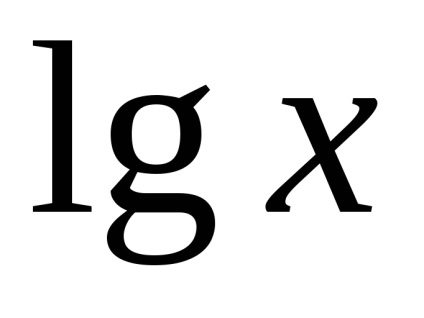
- 2 x (2 la puterea x) pow (x); -
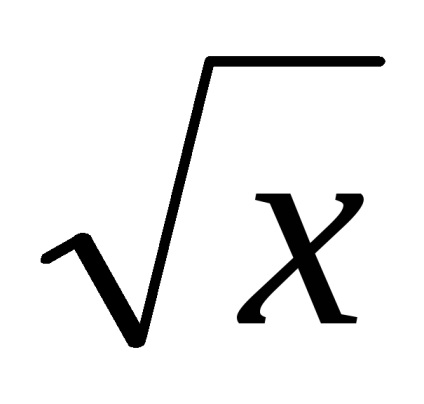
Matrici calcule în MATLAB
În sistemul MatLab, unitatea de bază de date este o matrice, deci sistemul dispune de un set extins de funcții și operații standard pentru prelucrarea matricelor, ceea ce permite:
- formează matrice noi de formă standard;
- efectuarea operațiunilor aritmetice matrice;
- calcula caracteristicile matricei și funcțiile matematice.
Pentru a forma noi matrici ale formularului standard, se folosesc următoarele funcții de sistem:
rand (M, N) - formează o matrice dreptunghiulară de dimensiune M x N, ale cărei elemente sunt numere aleatoare în intervalul (0,0; 1,0), Rand funcția fără parametri generează un număr aleatoriu în același interval.
(M, N) formează o matrice de identitate cu dimensiunea M × N.
zerourile (M, N) formează o matrice de dimensiune M × N, formată din zerouri.
diag (V) creează o matrice diagonală, în care elementele vectorului V sunt elemente ale diagonalei principale.
Operațiunile aritmetice matrice sunt reprezentate de următoarele:
A + B, A-B adunarea și scăderea matricei. Ambii operanzi ai acestei operații trebuie să aibă aceeași dimensiune, dacă sunt matrici. Unul dintre operanzi poate fi scalar.
A * B multiplicare matrice. Operația se efectuează în conformitate cu regulile de înmulțire a matricelor, numărul de coloane ale matricei A trebuie să fie egal cu numărul de rânduri ale matricei B.
A \ B diviziunea stângă a matricelor. Realizează decizia sistemului de ecuații algebrice liniare A * X = B. Numărul de coloane ale lui A trebuie să fie egal cu numărul de rânduri din B.
A / B este divizarea corectă a matricelor. Realizează decizia sistemului de ecuații algebrice liniare X * A = B.
X ^ P matricea este ridicată la o putere. Această operațiune în valoare P scalară ridică pătrat gradul R. matrice X Dacă X - valoarea scalară și P - o matrice pătrată, X ^ P X în matricea de grade F. Aceasta construiește operație este incorectă dacă ambii operanzi - matrice.
În MatLab, există operații matrice care sunt efectuate pe fiecare element al matricei, acestea fiind operații cum ar fi:
.elementary matrix multiplication.
.\ diviziunea stângă a matricelor.
. diviziunea dreaptă a matricelor.
.element-cu-element de construcție matrice.
Ambii operanzi ai acestor operații trebuie să aibă aceeași dimensiune sau una dintre ele trebuie să fie o cantitate scalară.
Operația "apostraf" calculează o matrice complexă de conjugat de transpunere.
Operația "dot apostraf" calculează matricea transpusă.
Sistemul conține funcții standard care vă permit să calculați diferite caracteristici ale matricelor:
det (A) calculează determinantul matricei;
urmări (A) calcularea urmei matricei;
rangul (A) care calculează rangul matricei;
inv (A) calculul matricei inverse.