Prin urmare, fluxul de lumină de la stele de magnitudine a șasea este de 100 de ori mai mic decât fluxul de lumină de la stele de prima magnitudine.
Cu cât strălucește mai mult steaua, cu atât este mai puțin magnitudinea ei aparentă.
Măsurătorile precise ale luminozității stelelor au necesitat introducerea unor magnitudine stelare fracționate și chiar negative. Cea mai strălucitoare stea a emisferei nordice a cerului este Vega (a-Lyra), magnitudinea sa stelară fiind de 0,14. Marimea aparenta a celei mai stralucitoare stele a intregului cer, Sirius, este de 1,58; Soarele - 26,7, iar Luna pe lună plină - 12,5.
Luminosity. Una dintre cele mai importante caracteristici fizice ale unei stele este luminozitatea L - aceasta este energia luminii emise de o stea pe unitate de timp. Fluxul luminos al unei stele depinde de distanța față de observator. Luminozitatea unei stele nu depinde de poziția observatorului. Luminozitatea Soarelui este de aproximativ 4 · 10 26 J / s. Aceasta este o cantitate foarte mare. Energia produsă de omenire de toate tipurile este mai mică de o mie de energie radiată de Soare într-o secundă.
Să găsim relația care conectează luminozitatea L a stelei cu magnitudinea sa aparentă și distanța față de observator.
Fie ca observatorul să fie la distanță R de stea. Înconjurăm steaua cu o sferă de rază R. Obținem fluxul luminos împărțind luminozitatea pe zona sferei:
Substituind expresia (16) în formula (15), obținem
Mărimea absolută. Imaginați-vă că toate stelele sunt situate la aceeași distanță de noi R = 10pc. Pentru a face acest lucru, cele mai apropiate stele ar trebui să se îndepărteze și majoritatea stelelor ne vor aborda. Comparând acum magnitudinile stelare vizibile ale stelelor, s-ar putea judeca care stea îi radiază mai multă energie.
Mărimea stelară absolută a M este acea magnitudine aparentă,
pe care o va avea steaua la o distanta de 10 p. Dacă înlocuim R = 10nk în (17), atunci în loc de r trebuie să scriem M
Scăderea (17) din (18), obținem
Conform formulei (19), este posibil să se determine magnitudinea stelară absolută dacă mărimea aparentă stelară m și distanța R la stea sunt cunoscute. Dacă Soarele este mutat la o distanță de 10pk, acesta se va transforma într-un asterisc cu magnitudinea stelei M = + 4,9. Mărimea absolută a lui Sirius este M = 1,4. Absolut magnitudinile stelare ale stelelor foarte luminoase sunt negative și ajung la M = -9. Cunoașterea magnitudinii stelare absolute a unei stele înlocuiește cunoașterea luminozității sale, precum și cunoașterea magnitudinii aparente stelare înlocuiesc cunoașterea fluxului luminos al stelei.
Reducerea mărimii stelare absolute cu o unitate înseamnă o creștere a luminozității stelei de 2,512 ori.
Partea a II-a. Exemple de rezolvare a problemelor.
Sarcina 1. Lampa din sticlă de lapte are forma unei mingi. Se suspendă la o înălțime h = 1 m deasupra centrului mesei rotunde cu un diametru de 2 m. Intensitatea luminii este de 50 cd. Determinați fluxul luminos al lămpii, iluminarea în centru și pe marginea mesei.
Problema 2. Un desen mare este fotografiat mai întâi cu un ac, apoi unele dintre detaliile sale într-o cantitate naturală. De câte ori este nevoie pentru a mări timpul de expunere când fotografiați componente?
Când fotografiați întregul desen, care este mult mai mare decât placa fotografică, imaginea este obținută aproximativ la focalizarea principală a obiectivului. Când fotografiați detaliile unei imagini în dimensiune completă, aceasta se obține prin plasarea obiectului la o distanță dublă focală de la obiectiv (la aceeași distanță, se obține imaginea de pe placa fotografică). Zona imaginii va crește cu un factor de unu.
Iluminarea plăcii fotografice scade cu același factor; prin urmare, expunerea ar trebui crescută de 4 ori.
Problema 3. O suprafață mată ideal cu coeficient de reflexie k = 0,9 are o iluminare de E = 30 lux. Scade luminozitatea.
Problema 4. În centrul unei încăperi pătrate de 25 m 2, o lampă se blochează. Presupunând că lampa este o sursă de lumină punctuală, găsiți la ce înălțime lampa să fie amplasată de pe podea, astfel încât iluminarea în colțurile camerei să fie cea mai mare.
Iluminarea în colțurile camerei.
Distanța de la lampă până la colțul camerei R. Valoarea (jumătate din diagonala pătratului pătrat al camerei), latura pătratului și înălțimea lămpii deasupra podelei h sunt legate de egalitatea evidentă
Pe baza (2), expresiile pentru iluminare pot fi scrise astfel: Pentru a găsi E maxim, luăm derivatul și echivalăm-l la zero:
Apoi va fi înălțimea h necesară
Problema 5. Iluminatorul de lumină ambientală produce un fascicul de lumină sub forma unui con trunchiat cu un unghi al soluției 2 = 40 °. Fluxul de lumină F al proiectorului este de 80 klm. Presupunând că fluxul de lumină este distribuit uniform în interiorul conului, determina intensitatea luminii I a luminii de proiecție.
Problema 6. Masa rotundă este iluminată de o lampă care atârna la altitudinea H deasupra centrului acesteia. Determinați distanța de la lampă la marginea zonei centrale, care reprezintă jumătate din fluxul de lumină care se află pe masă, dacă raza mesei este R. Luați în considerare lampa ca sursă de lumină punctuală.
Problema 7. O lentilă de colectare subțire cu o distanță focală f = 15 cm și un diametru D = 5 cm dă imaginea soarelui pe un ecran normal față de razele soarelui. Dacă nu luați în considerare pierderea de lumină a obiectivului, găsiți iluminarea medie a imaginii dacă luminozitatea soarelui este Bc = 1,5 10 9 cd / m 2.
Soluția. Iluminarea medie Ec este determinată din relație;
unde Φ este fluxul luminos care produce imaginea Soarelui pe ecran, iar S este zona imaginii. Deoarece imaginile sunt create de aceleași raze care au căzut prima pe lentilă, este posibil să se caute Φ ca fluxul de lumină care a survenit pe suprafața lentilei S1. prin urmare
unde E este iluminarea suprafeței lentilei de razele solare. Să o exprimăm prin strălucirea Soarelui dată în condiție, folosind legea iluminării și relația (11):
unde este raza Soarelui, a suprafeței sale vizibile (aria cercului și nu a emisferei!), R este distanța de la Pământ la Soare. Având în vedere că dimensiunile unghiulare (vizibile) ale soarelui pot fi foarte mici. Apoi, înlocuind valoarea lui E. determinată prin (3), în formula (2), obținem
Pentru a calcula zona S a imaginii Soarelui, ținem cont că va sta în planul focal al obiectivului. prin urmare
Acum, folosind formula (1), luând în considerare (4) și (5), avem
Înlocuind valorile numerice ale cantităților și realizând calculul, găsim Ec = 1,3 10 8 lux.
Partea a III-a. Sarcini pentru auto-soluționare.
1. În curte la o altitudine de 6 m, două lămpi sunt suspendate, distanța dintre lămpi este de 8 m. Calculați iluminarea la sol sub fiecare lămpi și în mijlocul acesteia. Puterea luminii fiecărei lămpi este de 500 cd.
2. Soarele este situat la o înălțime de 30 0 deasupra orizontului. Calculați iluminarea suprafeței, dacă se știe că atunci când Soarele se află la zenit, iluminarea suprafeței este de 100.000 lux.
3. Lumina de la un bec electric de 200 cd pas oferă un unghi de 45 0 la locul de muncă, iluminarea sa este de 141 lx. Caută:
1) la ce distanță de la locul de muncă este un bec,
2) la ce înălțime de la locul de muncă se blochează.
4. O lampă suspendată de tavan oferă intensitatea luminii de 60 cd în direcția orizontală. Ce flux de lumină cade pe imagine de 0,5 m 2. atârnând vertical pe perete la 2 m de lampă, dacă pe peretele opus există o oglindă mare la o distanță de 2 m de lampă?
6. La prânz în timpul echinocțiului de primăvară și toamnă, Soarele se află pe ecuator la zenit. De câte ori, în acest moment, iluminarea suprafeței Pământului la ecuator este mai mare decât iluminarea suprafeței pământului din Leningrad? Latitudinea din Leningrad 60 0.
7. Deasupra centrului mesei rotunde cu un diametru de 2 m este o lampă cu o intensitate luminoasă de 100 cd. Presupunând că lampa este o sursă punctuală de lumină, se calculează schimbarea iluminării marginii mesei cu o creștere treptată a lămpii în intervalul de 0,5 8. În centrul mesei rotunde de 1,2 m în diametru, există o lampă de masă de la o lampă electrică-rinichi la o înălțime de 40 cm de suprafața mesei. Deasupra centrului mesei la o înălțime de 2 m de la suprafața sa se află un candelabru fabricat din patru becuri. În ce caz va fi o iluminare mare pe marginea mesei (și în câte, de câte ori): când lampa de masă arde sau când candela arde? 9. Când fotografiați un obiect, subiectul este iluminat de o lampă electrică situată la 2 m de el. De câte ori ar trebui expusă expunerea dacă aceeași lampă este deplasată la 3 m de obiect? 10. Găsiți iluminarea de pe suprafața Pământului, cauzată de grinzile solare care cad în mod normal. Luminozitatea Soarelui este de 1,2. 10 9 nt. 11. Becul cu spirală cu intensitate luminoasă de 100 cd este închis într-un balon sferic mat, cu un diametru: 1) 5 cm și 2) 10 cm. În ambele cazuri, găsiți luminozitatea și luminozitatea lămpii. Pierderea luminii în coaja contorului ar fi neglijată. 12. O lampă în care un corp radiant servește ca un bec gol, cu un diametru de 3 mm, dă o intensitate a luminii de 85 cd. Găsiți strălucirea acestei lămpi dacă este făcut balonul sferic al lămpii: 1) din sticlă transparentă, 2) din sticlă mată. Diametrul balonului este de 6 cm. 13. Ce fel de iluminare dă lampa problemei anterioare la o distanță de 5 m cu o incidență normală de lumină? 14. Pe o foaie de hârtie albă de 20-30 cm, un flux luminos de 120 lm este normal la suprafață. Găsiți iluminarea, luminozitatea și luminozitatea foii de hârtie dacă coeficientul de împrăștiere este p = 0,75. 15. Care ar trebui să fie iluminarea hârtiei în problema anterioară, astfel încât luminozitatea acesteia să fie de 10 4 nt? 16. O foaie de hârtie cu dimensiunea de 10-30 cm este iluminată de lumina de la o lampă cu o forță de 100 cd, cu 0,5% din toată lumina trimisă de lămpile care cad pe ea. Găsiți ușurința acestei foi de hârtie.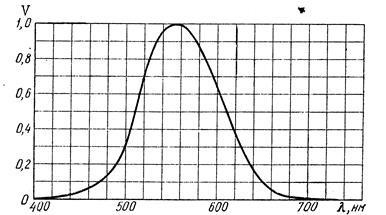
18. Un val lumină monocromatică cu a = 510 nm se află pe o suprafață plană de-a lungul valorii sale normale. Intensitatea valului = 0,32 W / m 2. Folosind imaginea din figura 4.
Un grafic al sensibilității spectrale relative a ochiului determină iluminarea E a suprafeței. La = 555 nm, fluxul de lumină în 1 lm corespunde unui flux de energie de 0,00160 W. Valoarea A = 0.00160 W / lm este uneori numită echivalentul mecanic al luminii.
19. Fluxul de lumină de 1 lm, format de radiația = 555 nm, corespunde unui flux de energie de 0,00160 W. Ce flux de energie corespunde unui flux luminos de 100 lm, format de radiație, pentru care sensibilitatea spectrală relativă a ochiului este V = 0.762?
20. Ce flux luminos corespunde fluxului energetic de 1,00 W, format din radiație, pentru care sensibilitatea spectrală relativă a ochiului este V = 0,142?
21. Să presupunem că escrocheria cuplat cu fluxul de energie de undă a luminii este uniform distribuit egal cu lungime de undă, adică. E. Ca Vaglen caz ar fi în acest caz, lumina curba de distribuție lungimi de undă brilor?
22. Un val monocromatic de lumină cu 5 = 510 nm sub incidență normală pe o anumită suprafață creează o iluminare de E = 100 lux. Determinați presiunea. Lumina exercitată pe suprafață dacă se reflectă jumătate din lumina incidentă.
23. Intensitatea (densitatea medie a fluxului luminos) a undelor luminoase monocromatice J = 100 lm / m 2. Frecvența valului = 3.69 10 15 s -1. Indicele de refracție al mediului în care se propagă valul este 1,50. Găsiți valorile amplitudinilor EM și NM ale intensităților câmpului electric și magnetic ale acestui val.
24. O sursă izotropă de lumină punct emise în toate direcțiile un flux de Φ = 1257 lm. Care este puterea luminii din această sursă?
25. paralel fasciculul de lumină care poartă o uniformă densitate de flux luminos J = 200lm / m 2 cade pe o suprafață plană, exterior din care se formează perpendicular pe direcția fasciculului unghi = 120 °. Care este iluminarea acestei suprafețe?
26. La o înălțime h = 3,00m deasupra punctului axisimetric funcția de intensitate sursă podea agățat este descrisă în interiorul și este zero la (I0 - constanta - unghiul format de fasciculul de lumină cu verticala). Iluminarea podelei sub sursa E = 100 lux. Determinați fluxul de lumină F. emis de sursă.
27. Punctați o sursă izotropă de lumină amplasată deasupra centrului mesei rotunde. Puterea sursei I = 50 cd, raza de masă R = 0,5 m, înălțimea sursei deasupra tabelului h = 1 m. Determinați:
1. Dependența iluminării E a mesei pe distanța r de la centru.
2. Valoarea iluminării: a) în centru, b) la marginea mesei.
3. Fluxul de lumină F. care se încadrează pe masă.
4. Ce fracțiune din fluxul total emis de sursă cade pe masă?
28. Așa cum ar trebui să depindă de unghiul dintre fasciculul și intensitatea luminoasă verticală I () sursa problemei pre- cedent fluxului incident pe masa F = 33 lm-lyalsya distribuite pe suprafața mesei uniform? Care va fi iluminarea E a mesei?
29. Luminozitatea unei suprafețe plane plane luminoase este descrisă de funcția (- unghiul cu suprafața normală la suprafață, - unghiul azimutului). Scrieți o expresie pentru luminozitatea L a acestei suprafețe.
30. Există o suprafață rotundă, uniformă, luminată, a cărei luminozitate (- constantă, egală cu - unghiul cu suprafața normală). Raza suprafeței este R = 10 cm. Găsiți fluxul de lumină FA emis de această suprafață.
31. Determinați la ce unghi la radiatorul normal kosi-nusny emite cel mai mare flux luminos.
32. Plot dependența de ieșire lumen luminos cosinus emiși emițător în interiorul unui con, a cărui axă este perpendiculară pe suprafața de destinatari, unghiul conului.
33. Deasupra centrului mesei rotunde a razei R pe înălțimea H = R, lampa atârnă cu puterea luminii. Construiește un grafic al dependenței iluminării suprafeței mesei de distanța r din centrul mesei. Pentru calcule, puneți. unde
34. Deasupra punctului A al suprafeței plane infinite, la o înălțime h există o sursă de lumină punctuală. Determinați raza inelului cu centrul în punctul A și lățimea dR. pe care scade fluxul luminos maxim.
35. Rezolvați problema anterioară pentru un mic emițător cosinus al cărui plan este paralel cu cel dat.
36. Lampa atârnă deasupra punctului A al suprafeței mesei la o înălțime H. Construiește o linie, când se deplasează peste lampa din punctul A creează iluminarea anterioară.
37. Sfera este iluminată de un fascicul paralel de lumină, creând în regiunea incidenței normale iluminarea lui Eo. Găsiți iluminarea medie a jumătății iradiate a suprafeței sferei.
38. Se calculează lungimea medie cu filament de tungsten luminozitatea de 3 cm și un diametru de 2 mm, în cazul în care intensitatea luminii într-o direcție perpendiculară pe axa helix ravna100 kd.
39. Lampă 100 cd închisă mat acoperă formă sferică de rază de 8 cm Se calculează luminozitatea medie a lămpilor în următoarele cazuri: a) absența pierderilor de flux de lumină în mată ;. b) în prezența unui factor de pierdere k = 0,1.
40. Un cilindru încălzit cu lungimea L și raza r are o temperatură constantă pe întreaga suprafață. Comparați intensitatea luminii emise în direcția axei cilindrului într-o direcție perpendiculară pe axa din mijlocul cilindrului.
41. O placă cu o suprafață S = 5 cm2 radiantă în ambele direcții are o luminozitate B = 106 cd / m 2. Se determină intensitatea medie a luminii emise de această placă.
42. Sfere omogene și cuburi din aceeași masă din același material radiază cu o luminozitate constantă pe toată suprafața. Care corp are o intensitate luminoasă medie mare?
43. Luminozitatea mingii fierbinți depinde de distanța față de ea?
44. Comparați luminozitatea discului solar și o suprafață mată albă ideal, situată perpendicular pe razele solare cu 3 cm.
45. Se determină reflexie medie a suprafeței lunare, în cazul în care luminozitatea medie a lunii pline este 2.5 10 martie cd / m 2 produs de iluminarii lumina directă a soarelui este 1.4 pot 10 lux.
46. Ce fel de iluminare în lux creează pe o stea normală la raze: a) zero magnitudine; b) prima valoare?
47. La o raza normala fata de razele suprafetei, luna plina creeaza o iluminare de 0,3 lux. Care este amploarea sa în acest moment?
8. Când lampa de masă arde, iluminarea marginii mesei este de 1,2 ori mai mare.