Broasca testoasă merge într-o curte și întâlnește un fluture acolo. Este frumos să ai portretul ei în colecția ei. Dar despre aripile care au forma unui cerc.
Cum de a învăța Turtle să deseneze un cerc? Poate ceva asemănător deja am atras? Bineînțeles. Amintiți-vă cum a privit corect pe ecran 20 de gonzi. A fost foarte asemănătoare cu un cerc.
Întrebarea 1: Cum se face poligonul cât mai aproape de un cerc
Puteți crește numărul laturilor. Dar pe ce număr de părți să rămână? Anterior, am constatat că pentru a construi un poligon închis, este necesar ca Turtle să se întoarcă în cele din urmă la punctul de plecare, i. E. a descris un unghi complet de 360 grade și a fost în aceeași orientare ca și cum ar fi fost. Dar poligonul se dovedește a fi "unghiular" dacă numărul laturilor nu este suficient de mare.
Întrebarea 2: Câte părți au nevoie pentru ca un poligon să ne arate un cerc?
Să încercăm să construim poligonul corect cu numărul de laturi 360, folosind comanda "REPEAT".
Întrebarea 3. Câte repetări aveți nevoie pentru a construi acest poligon?
Nu este dificil să se calculeze unghiul de rotație pe care Turtle ar trebui să se întoarcă o dată (ne amintim cum a fost obținut unghiul de rotație pentru construirea a 5, 6, etc., poligoane regulate) - 1 grad. Ce lungime a laturii de ales? Dacă faceți 20 de pași - cercul nu se potrivește pe ecran și pe lângă acesta va fi un poligon pronunțat, nu un cerc.
Întrebarea 4: Câți pași trebuie să facă Teenagerul pentru a desena o parte a acestui poligon?
1 pas este cel mai potrivit număr. Astfel: numărul de repetări este de 360; lungimea laturii - 1 pas; unghiul de rotație pentru o repetare este de 1 grad. Totul este cunoscut pentru a desena un cerc, primul cerc pe care l-am construit. Să numim acest cerc un cerc de prima dimensiune. Vom scrie această procedură.
Acesta este un mediu1
REPEAT 360 [VP 1 PR 1]
END
O parte a unei aripi este gata. Este ușor de văzut că exact aceeași parte se găsește și în cealaltă aripă.
Întrebarea 5: Care este diferența?
A plecat. Ce trebuie să schimb pentru a desena partea stângă a aripii? Desigur, direcția turnului. Partea din stânga va fi desenată astfel:
ACEASTA ESTE ENVIRONMENT1_LEVER
REPEAT 360 [VP 1 LV 1]
END
Acum trebuie să învățăm Țestoasa să tragă un cerc mai mic decât CIRCULA1. deoarece fiecare aripa constă din două cercuri. Ce se poate schimba? Dacă schimbăm numărul de pași, putem să le mărim doar, dar cercul va fi și mai mare. Să încercăm să experimentăm dimensiunea unghiului. Este clar că nu o putem reduce. Ce se va întâmpla dacă creșteți unghiul?
Fie ca VOLL1 să fie unghiul în 1 0. și UGOL2 - 2 0. Acum, să vedem cum se va comporta Teenage atunci când execută un număr de ori comenzile
[EP 1 PR 1] și [VI 1 PR 2].
Dar înainte de a face acest experiment, trebuie să discutăm următorul punct: Broasca testoasă se va roti 1 dată la un unghi de 2 0 și în cele din urmă trebuie să descrie unghiul total de 360 °.
Întrebarea 6. Câte repetiții vor fi suficiente pentru comenzile [VI 1 PR 2]? Este ușor de calculat că numărul de repetiții va fi de 180. Acum, puteți trece la experiment și puteți verifica modul în care Turtle se va comporta atunci când execută comenzi
REPEAT 360 [VI 1 PR 1] și REPEAT 180 [VI 1 PR 2]
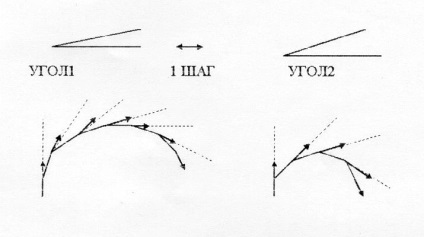
După cum vedem din acest experiment, în cazul în care unghiul este 2 0. atunci Turtle descrie un cerc mai mic (amintiți-vă din viață atunci când trebuie să vă întoarceți la un unghi mai mare dacă vă învârțiți în jurul stadionului sau o nisip rotund în curte?).
Întrebarea 7: Ce concluzie putem trage din acest experiment?
Cu cât unghiul de rotație este mai mare cu fiecare repetare, cu atât este mai mică circumferința. Aceasta înseamnă că pentru a construi a doua parte a aripii (cercul este jumătate la fel de mare ca și circumferința 1), Turtle va repeta comenzile [VI 1 PR 2].
Acum, să scriem procedura pentru desenarea celui de-al doilea cerc. Să numim un cerc al celei de-a doua dimensiuni.
Acesta este un mediu2
REPEAT 180 [VP 1 PR 2]
END