O transmisie simplă a angrenajului va fi numită mecanism mecanic cu trei legături, compus din două trepte și un raft. Să luăm în considerare modul în care este posibil să se exprime raportul de transmisie în transmisii simple cu angrenaje la diferite aranjamente ale axelor roților lor în spațiu.
P eradacha s pallalmelnymi i om sokol'ko s tsilin d richeskaya p yer e și h și d). La angrenajele cu axe paralele ale roților, există cercuri care, atunci când mișcarea este transmisă, se rotește unul pe altul fără alunecare. Strict vorbind, dacă ținem cont de dimensiunea roților în direcția axelor lor (lățimea jantei), apoi, în fapt, nu există nici o atingere de cercuri și cilindri în imaginea lor. Cu toate acestea, în secțiunea acestor cilindri, orice plan perpendicular pe axele lor are același model de tangență a cercurilor. Toate proprietățile de transmisie sunt determinate de proprietățile acelor elemente care sunt situate în planul specificat (deci un astfel de transfer este numit plat). Cercurile care se ating unul de celălalt se numesc centroid. deoarece circumferința unei roți este locul geometric al centrelor de rotație relativă instantanee a celeilalte roți. În Fig. 2.2 prezintă o astfel de transmisie. În el roata 1 se rotește în jurul centrului O1. și roata 2 - în jurul centrului O2. Cercurile lor centroid se ating reciproc la punctul P. Direcția de rotație a roților este indicată prin săgeți. La punctul P, viteza circumferențială a roților sunt aceleași și sunt determinate de produsul dintre vitezele unghiulare ale roților pe razele centroida cercurilor 1 și 2 m. F. Și respectiv. Deoarece aceste viteze sunt egale, avem egalitatea
din care rezultă că raportul de transmisie poate fi exprimat în raport cu raportul dintre razele cercurilor centroidice, adică,
Semne „+“ și „-“ înainte de a raportului raze a apărut datorită faptului că, în contrast cu viteza unghiulară, raze nu poate fi negativă, iar semnul „-“ se referă la acest sistem, un semn „+“ ar fi cazul spargerea interioară a roților.
Dacă centroidul este un cerc de divizare, atunci raza lor poate fi exprimată după cum urmează. Lungimile cercurilor centrice S1 ale primei roți și S2 ale celei de-a doua roți sunt determinate de expresiile respective:
S1 = 2 · π · 1 = p · 1 și S2 = 2 · π · 2 = p · 2. unde p este pasul roților de-a lungul cercului de divizare, adică distanța dintre aceleași puncte ale doi dinți învecinați. măsurată pe cercul de separare, 1 și 2 - numărul de dinți ai roților date, (la fel ca numărul de trepte).
Raportul dintre pasul cercului de divizare și numărul π este numit modulul de angrenaj, care este notat cu litera latină m. Modulul, la fel ca pasul, este același pentru roțile care se cuplează. Este măsurată în milimetri și prin aceasta sunt exprimate toate dimensiunile dinților (magnitudinea modulelor este determinată de standard). Înlocuind acum în loc de raze în expresia înregistrată anterior a raportului, valorile lor găsite mai sus, după o reducere de 2 și m. în sfârșit ajungem
Adică, raportul de transmisie al unui tren simplu de transmisie cu osii roților paralele poate fi exprimat ca raportul invers al numărului de dinți ai roților.
PREGĂTIREA SUSPENDĂRII SUSPENDĂ A ȘCOLELOR DURABILE up part). Teșitura dinții roților dințate tăiate în conuri trunchiate 1 și 2 pe fiecare alte pe PO generatoarea comune și reverberează unul pe celălalt fără să alunece în jurul acestuia (fig. 2.3). Roțile se rotesc în raport cu coloana cu viteze unghiulare și în jurul axelor care coincid cu axele conurilor. Jumătate din unghiurile conurilor sunt marcate cu litere și, prin urmare, suma acestor unghiuri formează unghiul interaxial al transmisiei. care este.
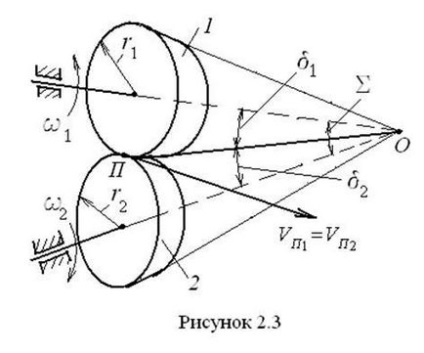
Bazele de conuri cu raze și atinge reciproc la punctul P și au aceleași viteze în ea: și. De la egalitatea vitezelor circumferențiale pe care le avem. Deoarece axele conurilor sunt perpendiculare pe baza lor, putem scrie și. Prin urmare,
Lungimile cercurilor de raze sunt egale cu, respectiv,. unde este treapta pintenilor și - numărul de dinți ai roților. Rezumând toate calculele, vom scrie în cele din urmă toate variantele de exprimare a raportului de transmisie în această unelte :.
PEREDACHA cu pekere krushchina în aushchim și I osmykoloe s (peredadchavint despre wi și k olo l e și m). În această unelte, dinții roților sunt tăiați pe cilindri rotunzi, iar axele roților sunt traversate la un unghi de intersecție. în cazul general, nu sunt egale cu 90 ° și sunt distanțate una de alta la distanța cea mai mică (Figura 2.4a). În acest caz, dinții formează unghiuri față de axele roților - prima roată și - cea de-a doua roată (Figura 2.4b), astfel încât să rămână egalitatea.
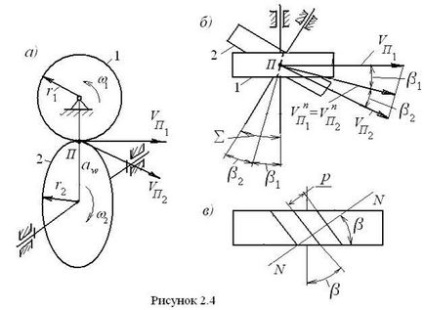
Vitezele circumferențiale ale roților din această roată, diferite în mărime și în direcție, sunt determinate de formulele:. Deoarece unghiul interaxial din transmisie este. iar vitezele circumferențiale ale roților la punctul P sunt perpendiculare pe axele roților, atunci unghiul dintre ele este de asemenea egal. așa cum se vede în Fig. 2.4 b. În această figură, linia punctată arată linia dinților de contact ai roților. Eliminăm perpendicular pe această linie prin punctul P al acestei linii și proiectăm vitezele u pe ea. după ce au primit componentele lor normale, coincisând între ele în mărime și direcție, adică. Așa că ajungem la egalitate. din care urmează
Ultimul termen al acestei egalități indică faptul că raportul de transmisie poate fi influențat nu numai de razele cilindrilor roților de contact, ci și de unghiurile de înclinare ale dinților. Să vedem cum altfel este posibil să exprimăm raportul de transmisie al acestei transmisii. Pentru aceasta ne întoarcem la Fig. 2.4 c. care arată o roată cu dinți oblici care formează un unghi cu axa roții. Vom diseca roata printr-un plan perpendicular pe linia dintelui, a cărui urmă este marcată de linia NN din figură. În acest plan, pasul roții este indicat de litera p. Este aceeași pentru ambele roți, prin urmare, modulele roților m în acest plan sunt, de asemenea, aceleași. În planul final al roții perpendiculare pe axa sa, așa cum se poate vedea din figură, pasul este determinat de raport. Aceste calcule și argumente sunt valabile pentru ambele roți, astfel încât să putem scrie mai departe expresiile pentru razele cilindrilor în acest fel
Înlocuirea acestor expresii în relația anterioară, după abrevieri, obținem în cele din urmă
Astfel, am constatat că într-o transmisie dințată simplă, indiferent de localizarea roții sale axe în spațiu, raportul de transmisie (sau raportul de transmisie) poate fi definit ca raportul dintre numărul de dinți de angrenare adoptate ca un sclav la numărul de dinți de angrenare adoptate ca lider .
Un caz special de angrenaj cu roți cu șuruburi este un angrenaj cu melc. în care una dintre roți poate avea doar un dinte și se numește un vierme. Atunci când un dinte - este un șurub cu un singur fir, cu doi dinți - .. dublu-threaded vierme, etc. Alte roți de transmisie numita roata vierme. În această transmisie raport de transmisie este determinată de o regulă generală stabilită mai sus, adică, raportul de transmisie al viermelui (servește întotdeauna ca maestru) la roata de vierme este egal cu raportul dintre numărul de dinți de angrenare cu numărul de robinete de vierme.