Interferența este una dintre cele mai strălucite manifestări ale naturii luminoase a luminii. Acest fenomen interesant și frumos este observat când două sau mai multe grinzi de lumină sunt suprapuse. Intensitatea fasciculelor de lumină în regiunea de suprapunere are caracter de benzi alternative de lumină și întuneric, intensitatea maximelor este mai mare și minimele mai puțin decât suma intensităților fasciculului. Atunci când se utilizează alb franje de interferență de lumină sunt vopsite în diferite culori ale spectrului. Cu fenomene de interferență pe care le întâlnim destul de des: pete de ulei de culoare pe asfalt, pictura geamuri de congelare de sticlă, modele de fantezie colorate pe aripile unor fluturi și gândaci - toate acestea este o manifestare a interferenței luminii.
I. Primul experiment pentru a observa interferența luminii în condiții de laborator aparține lui I. Newton. El a observat un model de interferență care apare atunci când lumina se reflectă într-un strat subțire de aer între o placă de sticlă plană și o lentilă planoconvex cu o rază mare de curbură (Figura 3.7.1). Modelul de interferență a fost în formă de inele concentrice, numite inele Newton (Figura 3.7.2).
Figura 3.7.1. Observarea inelelor lui Newton. Interferența apare când se adaugă valuri, reflectate de ambele părți ale stratului de aer. "Rays" 1 și 2 sunt direcțiile de propagare a undelor; h este grosimea spațiului de aer
Figura 3.7.2. Inelele lui Newton cu lumină verde și roșie
Newton nu a putut din punctul de vedere al teoriei corpusulare să explice de ce apar inelele, dar a realizat că acest lucru se datorează unei anumite periodicități a proceselor luminoase (a se vedea § 3.6).
Primul experiment de interferență, explicat pe baza teoriei undelor luminoase, a fost experiența lui Jung (1802). În experimentul lui Jung, lumina provenită de la sursă, care a servit ca o fantă îngustă de S., a căzut pe ecran cu două fante scurte S1 și S2 (Figura 3.7.3). Trecând prin fiecare dintre sloturi, fasciculul luminos sa lărgit datorită difracției, astfel încât pe ecranul alb E fasciculele luminoase au trecut prin sloturile S1 și S2. suprapunere. În zona de suprapunere a fasciculelor luminoase, a fost observat un model de interferență sub forma benzilor alternante de lumină și întunecate.
Figura 3.7.3. Modelul de interferență al lui Jung
Jung a fost primul care a realizat că interferența nu poate fi observată atunci când valurile sunt adăugate din două surse independente. Prin urmare, în experiența sa, fantele S1 și S2. care, în conformitate cu principiul Huygens pot fi considerate ca surse de valuri secundare iluminate de sursa de lumină S. Într-un aranjament simetric de fante undelor secundare emise de sursele S1 și S2. sunt în fază, dar aceste unde se deplasează către punctul de observare P diferite distanțe r1 și r2. În consecință, fazele oscilațiilor produse de undele surse S1 și S2 la punctul P. sunt în general diferite. Astfel, problema interferenței valurilor se reduce la problema de a adăuga oscilații cu aceeași frecvență, dar cu diferite faze. Declarația conform căreia valurile din sursele S1 și S2 se propagă independent unul de celălalt, iar la punctul de observare se adaugă pur și simplu, este un fapt experimental și se numește principiul suprapunerii.
Un val monocromatic (sau sinusoidal). propagând în direcția vectorului de rază. este scris ca
unde a este amplitudinea undei, k = 2π / # 955; Este numărul de val, # 955; Este lungimea de undă, # 969; = 2π # 957; Este frecvența circulară. În problemele optice, E trebuie înțeleasă ca modul al vectorului intensității câmpului electric al valului. Atunci când două valuri sunt adăugate la punctul P, oscilația rezultată are loc și la frecvență # 969; și are o anumită amplitudine A și o fază # 966;:
Nu există dispozitive care să poată monitoriza schimbările rapide în câmpul undei de lumină în intervalul optic; Cantitatea observată este fluxul de energie, care este direct proporțional cu pătratul amplitudinii câmpului electric al valului. Cantitatea fizică egală cu pătratul amplitudinii câmpului electric al valului este denumită de obicei intensitatea. I = A 2.
Transformările trigonometrice simple duc la următoarea expresie pentru intensitatea oscilației rezultate în punctul P:
Formulele (*) și (**) sunt universale. Acestea sunt aplicabile oricărei scheme de interferență în care se adaugă două valuri monocromatice de aceeași frecvență.
Dacă în schema lui Young se desemnează prin y deplasarea punctului de observare din planul simetriei, atunci pentru cazul în care d < Când deplasarea de-a lungul axei de coordonate y este egală cu lățimea marginii de interferență # 916; l. adică atunci când se deplasează de la o maximă de interferență la alta, diferența în cale # 916; variază cu o lungime de undă # 955; Prin urmare, unde # 968; Este unghiul de convergență al "razelor" în punctul de observare P. Vom efectua o evaluare cantitativă. Să presupunem că distanța d dintre sloturile S1 și S2 este de 1 mm, iar distanța dintre fante la ecranul E este L = 1 m, apoi # 968; = d / L = 0,001 rad. Pentru lumina verde (# 955; = 500 nm), ajungem # 916; l = # 955; / # 968; = 5,10 5 nm = 0,5 mm. Pentru lumina roșie (# 955; = 600 nm) L = 0,6 mm. În acest fel, Jung a măsurat pentru prima dată lungimile undelor luminoase, deși precizia acestor măsurători a fost mică. Trebuie subliniat că în optica undelor, spre deosebire de optica geometrică, conceptul unei raze de lumină își pierde semnificația fizică. Termenul "fascicul" este utilizat aici pentru scurtcircuit pentru a indica direcția propagării undelor. În viitor acest termen va fi folosit fără cotare. În experimentul Newton (figura 3.7.1), cu o incidență normală a undelor pe o suprafață plană a lentilei, diferența de cale este aproximativ egală cu dublul grosimii 2h a spațiului dintre obiectiv și plan. Pentru cazul în care raza de curbură R a lentilei este mare în comparație cu h. putem obține aproximativ: unde r este deplasarea de la axa simetriei. Atunci când se scrie o expresie pentru diferența de cale, ar trebui să se țină seama de faptul că undele 1 și 2 sunt reflectate în condiții diferite. Primul val se reflectă din granița dintre sticlă și aer și cel de-al doilea val se reflectă din granița aer-sticlă. În al doilea caz, faza de oscilații a undelor reflectate se modifică cu π, ceea ce echivalează cu creșterea diferenței de cale prin # 955; / 2. Prin urmare La r = 0, adică în centrul (punctul de contact) # 916; = # 955; / 2; prin urmare, în centrul inelelor lui Newton există întotdeauna un minim de interferență - un punct întunecat. Radiografia inelelor întunecate ulterioare este dată de Această formulă ne permite să determinăm experimental lungimea de undă a luminii # 955, dacă este cunoscută raza de curbură R a lentilei. Problema coerenței valurilor. Teoria lui Jung a făcut posibilă explicarea fenomenelor de interferență care apar atunci când se adaugă două valuri monocromatice de aceeași frecvență. Cu toate acestea, experiența de zi cu zi învață că interferența lumii în realitate nu este ușor de observat. Dacă două becuri identice ard într-o cameră, atunci în orice punct se adaugă intensitatea luminii și nu se observă interferențe. Se pune întrebarea, în ce cazuri este necesar să se adauge tensiunea (ținând seama de relațiile de fază), în care - intensitatea undelor, adică pătraturile forțelor câmpului? Teoria interferenței undelor monocromatice nu poate da un răspuns la această întrebare. Undele reale de lumină nu sunt strict monocromatice. Datorită cauzelor fizice fundamentale, radiația are întotdeauna un caracter statistic (sau aleator). Atomii sursei luminoase radiază independent unul de celălalt în momente aleatorii, iar radiația fiecărui atom are un timp foarte scurt (# 964; ≤ 10-8 s). Radiația rezultată a sursei în fiecare moment al timpului constă în contribuția unui număr imens de atomi. După un timp de comandă Întregul set de atomi radianți este actualizat. Prin urmare, radiația totală va avea o amplitudine diferită și, mai important, o fază diferită. Faza valului emise de sursa reală de lumină rămâne aproximativ constantă numai pe intervale de timp de ordinul lui # 964; Separați "resturile" radiațiilor de durată # 964; numite trenuri. Zugi au o lungime spațială egală cu c În care c este viteza luminii. Oscilațiile în trenurile diferite nu sunt coerente între ele. Astfel, valul real al luminii este o secvență de trenuri de undă cu o fază care variază aleatoriu. Este obișnuit să spunem că oscilațiile din trenurile diferite sunt incoerente. Interval de timp În care faza oscilațiilor rămâne aproximativ constantă, se numește timpul de coerență. Interferențele pot apărea numai atunci când se adaugă oscilații coerente, adică oscilații legate de același tren. Deși fazele fiecăreia dintre aceste oscilații sunt, de asemenea, supuse schimbărilor aleatorii în timp, dar aceste schimbări sunt aceleași, astfel încât diferența de fază a oscilațiilor coerente rămâne constantă. În acest caz, se observă un model de interferență stabil și, prin urmare, principiul superpoziției câmpurilor este îndeplinit. Când se adaugă oscilațiile incoerente, diferența de fază se dovedește a fi o funcție aleatorie a timpului. Fragmentele de interferență se confruntă cu mișcări neregulate de la o parte la alta și în timp În testarea lor, care în experimentele optice este mult mai lungă decât timpul de coerență (# 916; t >> # 964;), există o mediere completă. Dispozitivul de înregistrare (ochi, placă fotografică, fotocelule) stabilește la punctul de observare valoarea medie a intensității egală cu suma intensităților I1 + I2 ale ambelor oscilații. În acest caz, legea adaosului de intensități este îndeplinită. Astfel, interferența poate să apară numai atunci când se adaugă oscilațiile coerente. Valurile care creează oscilații coerente la punctul de observare sunt numite și oscilații coerente. Valurile din două surse independente sunt incoerente și nu pot da interferențe. T. Jung a ghicit intuitiv că, pentru a obține interferența dintre lumină, trebuie să divizăm valul de la sursă în două valuri coerente și apoi să observăm rezultatul adunării lor pe ecran. Acest lucru se face în toate schemele de interferențe. Cu toate acestea, chiar și în acest caz, modelul de interferență dispare în cazul diferenței de cale # 916; va depăși lungimea de coerență c # 964;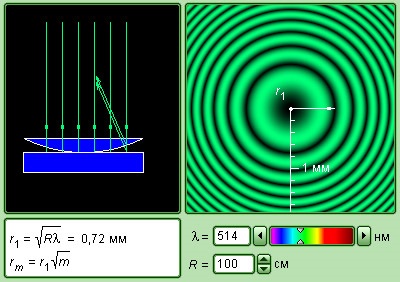
Modelul. Inelele lui Newton