5.2. Operatorul buclă în timp
Limbajul de programare MatLab are doi operatori buclă: în timp ce și pentru. Cu ajutorul lor, de exemplu, se efectuează programarea algoritmilor recurenți. numărarea sumei seriei, enumerând elementele matricei și multe altele.
În cel mai simplu caz, o buclă din program este organizată folosind instrucțiunea while, care are următoarea sintaxă:
Există o expresie condițională similară cu cea utilizată în cazul în care declarația și bucla în timp ce se execută atâta timp cât condiția este adevărată.
Trebuie remarcat faptul că, în cazul în care condiția este falsă înainte de bucla, declarațiile incluse în ciclul nu sunt îndeplinite nici măcar o dată.
Iată un exemplu de modul în care buclă în timp funcționează pentru a calcula suma unei serii:
S = 0; % din valoarea inițială a sumei
i = 1; Contor sumă%
în timp ce i 20% dacă S> 20,
pauză; % atunci ciclul se încheie
capăt
sfârșitul sfârșitului ciclului%
disp (S); % afișare a sumei 21 de pe ecran
În acest exemplu, a doua condiție de terminare a buclei când S este mai mare de 20, se înregistrează în ciclul și cu operatorul părăsește funcția ciclu pauză disp (), în timp ce în picioare imediat după ciclu.
Cel de-al doilea operator care controlează executarea ciclului continuu vă permite să săriți executarea fragmentului de program după el. De exemplu, trebuie să calculați suma elementelor matrice
a = [1 2 3 4 5 6 7 8 9];
cu excepția unui element cu index 5. Un astfel de program poate fi scris după cum urmează:
S = 0; % din valoarea inițială a sumei
a = [1 2 3 4 5 6 7 8 9]; % array
i = 0; % număr indice matrice
în timp ce i =.
capăt
Să luăm în considerare activitatea acestui ciclu utilizând exemplul algoritmului pentru găsirea valorii maxime a unui element într-un vector:
a = [3 6 5 3 6 9 5 3 1 0];
m = a (1); % valoare maximă curentă
pentru i = 1: lungimea (a)% ciclu de la 1 la capătul vectorului c
% pasul 1 (implicit)
dacă m m,
m = a (i); % atunci m = a (i)
capăt
final sfârșitul% pentru buclă for
disp (m);
În acest exemplu, buclă pentru setarea contului i și modificarea valorii sale de la 1 la 10 în trepte de 1. Rețineți că dacă mărimea pasului nu este specificată în mod explicit. atunci este luată în mod prestabilit egală cu 1.
În următorul exemplu, luați în considerare implementarea algoritmului pentru deplasarea elementelor vectorului spre dreapta, adică Cel mai penultim element este pus în locul ultimului, următorul - în locul penultimului, etc. până la primul element:
a = [3 6 5 3 6 9 5 3 1 0];
disp);
pentru i = lungime (a): - ciclu 1: 2% de la 10 la 2 în trepte de -1
a (i) = a (i-1); % schimbăm elementele vectorului a
final sfârșitul% pentru buclă for
disp);
Rezultatul programului
3 6 5 3 6 9 5 3 1 0
3 3 6 5 3 6 9 5 3 1
Exemplul de mai sus arată că pentru a implementa o buclă cu un contor de la o valoare mai mare la una mai mică, trebuie să specificați în mod explicit pasul, în acest caz, -1. Dacă nu faceți acest lucru, bucla se va termina imediat și programul nu va funcționa corect.
6. Soluții ale ecuației
6.1. Metodă grafică pentru rezolvarea ecuațiilor
Afișarea mai multor grafice simultan oferă cea mai simplă modalitate de a găsi valoarea aproximativă a soluției.
Acest grafic prezintă graficele funcțiilor y = sin (t) / t și (x / 5) 2 + y 2 = 1. Deoarece nu este dificil de observat aceste funcții au trei puncte de intersecție.
6.2. Căutați soluția de ecuație
Metoda grafică poate aproxima numai soluția. Pentru a găsi soluția mai precis în pachetul MatLAB, utilizați funcția fsolve (ecuație, valoare inițială). Mai târziu, vom învăța cum să rezolvăm un sistem de ecuații utilizând această funcție. În cel mai simplu caz, ecuația rezolvată poate fi specificată în citate simple. de exemplu: 'x * x-abs (x)'. Dar această funcție are trei soluții, prezentate în Fig.
Soluția pe care funcția fsolve o găsește în acest caz va fi determinată de valoarea inițială de unde începe procedura iterativă pentru găsirea soluției. De exemplu:
fsolve ('x * x-abs (x)', - 2), ans = -1,0000;
fsolve ('x * x-abs (x)', 0,6), ans = 1,0000;
fsolve ( 'x * x-abs (x)', 0,4), ans = 7.9062e-008.
Funcția fsolve continuă procedura iterativă până când găsește o soluție cu precizia specificată. Prin urmare, în exemplul nostru am obținut 7.9062e-008 în loc de 0.
În cazul funcțiilor mai complexe, este mai convenabil să le reprezentăm sub forma unui fișier M. Apoi, ca primul parametru al funcției fsolve, numele acestui fișier este înlocuit în ghilimele simple.
7. fișiere M
M-fișiere în MatLab sunt de două tipuri: program de fișiere (Script M-Files), care conține o secvență de comenzi, și funcțiile de fișier, (Funcție M-Files), care descrie funcțiile definite de utilizator.
7.2. programul de fișiere
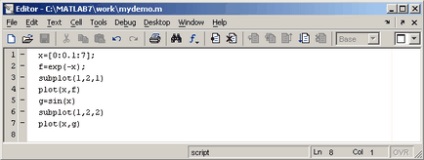
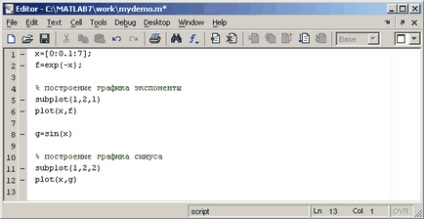
7.3. Funcție fișier
Funcțiile M sunt fișiere M care permit prezența argumentelor de intrare și ieșire. Ele lucrează cu variabile în zona proprie de lucru, diferită de aria de lucru a sistemului MATLAB.
Funcția medie este un fișier M destul de simplu care calculează valoarea medie a elementelor vectoriale:
funcția y = media (x)
% AVERAGE Valoarea medie a elementelor vectoriale.
% AVERAGE (X), unde X este un vector. Calculează valoarea medie a elementelor vectoriale.
% Dacă argumentul de intrare nu este un vector, se generează o eroare.
[m, n] = dimensiunea (x);
dacă (
((m == 1) | (n == 1)) (m == 1 n == 1))
eroare ("Matricea de intrare trebuie să fie un vector")
capăt
y = suma (x) / lungimea (x); % Calculul real
Încercați să introduceți aceste comenzi într-un fișier M numit average.m. Funcția medie permite o singură intrare și un singur argument de ieșire. Pentru a apela funcția medie, trebuie să introduceți următorii operatori:
exempluȘirul pentru determinarea mediei este:
funcția y = media (x)
aici:
funcția - cuvântul cheie care definește funcția M;
y este argumentul de ieșire;
media - numele funcției;
x este argumentul de intrare.
Fiecare funcție din sistemul MATLAB conține un șir de definire a funcției similar cu cel dat.
Dacă funcția are mai mult de un argument de ieșire, lista argumentelor de ieșire este plasată în paranteze pătrate. Argumentele de intrare, dacă sunt prezente, sunt plasate în paranteze. Ciclurile sunt folosite pentru a separa argumentele din listele de intrare și de ieșire.
funcție [x, y, z] = sferă (theta, phi, rho)
Numele variabilelor de intrare pot, dar nu trebuie să se potrivească, numele specificate în șirul de definiție a funcției.
% AVERAGE Valoarea medie a elementelor vectoriale
Numele funcțiilor M. În sistemul MATLAB, aceleași restricții se aplică și numelor funcțiilor M în funcție de numele variabilelor - lungimea lor nu trebuie să depășească 31 de caractere. Mai exact, numele poate fi mai lung, dar sistemul MATLAB ia în considerare doar primele 31 de caractere. Numele funcțiilor M trebuie să înceapă cu o literă; Caracterele rămase pot fi orice combinație de litere, numere și subliniere.
Numele fișierului care conține funcția M este compus din numele funcției și din extensia ".m".
average.m
Dacă numele fișierului și numele funcției din șirul de definiție a funcției sunt diferite, atunci numele fișierului este utilizat și numele intern este ignorat. Deși numele funcției definit în șirul de definire a funcției poate să nu fie același cu numele fișierului, este recomandat să folosiți același nume.