În practică, se găsesc probleme pentru determinarea extremumului funcționalilor atunci când punctele finale ale curbelor variabile sunt fixe, libere sau aparțin unor varietăți. La aceste puncte de frontieră, trebuie îndeplinite așa-numitele condiții de transversalitate.
Condițiile de transversalitate pentru un interval fix T:
Este necesar să se investigheze împreună cu valorile limită pentru x (t), care pot fi fixate sau libere (figura 1).
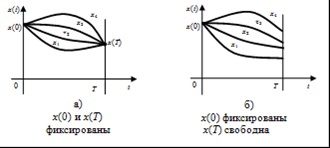
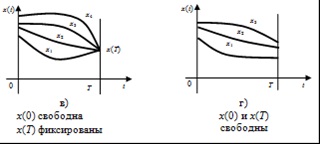
Fig. 1.2.1 Funcțiile admisibile x (t) în funcție de condițiile limită
Dacă valoarea limită x (tpp) este dată (în cazul în care trp = 0 sau T), atunci variația trebuie să fie zero și valoarea derivatului nu este suprapusă.
Dacă valoarea limită x (tpp) este liberă, atunci variația poate fi arbitrară, deci trebuie să fie zero [2].
Considerăm diferite probleme pentru un interval fix de optimizare T.
1. Valorile inițiale x (0) și finale x (T) ale cantității de ieșire sunt date (o problemă cu punctele de graniță fixe, figura 1.2.1, a).
În această problemă, toate curbele posibile x (t), dintre care extrema x * (t) este căutată, trebuie să înceapă și să se termine la anumite puncte. Variațiile (0) și (T) sunt zero și nu se aplică nicio restricție pentru derivatul măsurii de eroare la limitele intervalului. Constantele C1, C2 se găsesc din condițiile limită pentru x (0), x (T) și nu se utilizează condițiile de transversalitate.
2. Valoarea inițială x (0) a cantității de ieșire este fixă, iar valoarea finală x (T) este liberă (o problemă cu o limită dreaptă în mișcare, Fig.12.1, b).
Deoarece x (T) poate lua valori arbitrare, variația (T) poate fi de asemenea arbitrară, prin urmare condiția de transversalitate va fi satisfăcută numai dacă derivatul
Astfel, cele două condiții de limită x (0) și ne permit să găsim valorile constantelor de integrare C1, C2.
Condițiile limită ale problemei cu un punct inițial neangajat x (0) și o fixă finită x (T) (o problemă cu o limită stângă în mișcare, Fig.1.2.1, c) sunt definite în mod similar.
Pe limita stângă, variația (0) poate fi oricare, atunci. Din această condiție și valoarea limită x (T) sunt constantele de integrare.
4. Valoarea inițială x (0) și valoarea finală x (T) a cantității de ieșire sunt libere (o problemă cu punctele de graniță nelimitate, figura 12.1, d).
Deoarece variațiile (0) și (T) pot fi arbitrare, condițiile de transversalitate implică faptul că derivatul măsurii de eroare trebuie să dispară la limitele
Constatările de integrare C1 și C2 sunt determinate din aceasta.
Lăsați următorul lucru funcțional
unde: funcția caracterizează starea sistemului la momentul t = T.