Un desen este primul și foarte important pas în rezolvarea unei probleme geometrice. Care ar trebui să fie desenul piramidei drepte?
Mai întâi, să ne reamintim proprietățile designului paralel.
- segmentele paralele ale figurii sunt reprezentate de segmente paralele;
- se păstrează raportul dintre lungimile segmentelor drepte paralele și segmentele unei linii drepte.
Desenarea piramidei drepte triunghiulare
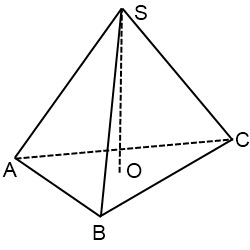
Centrul triunghiului drept este punctul de intersecție a medianilor triunghiului. Deoarece mediana la punctul de intersecție sunt divizate într-un raport de 2: 1, numărate de la vârf, vârf de bază se combină mental cu mijlocul laturii opuse, aproximativ se împarte în trei părți, și două părți în regiunea consemnului vertex. Din acest punct în sus, tragem o perpendiculare. Aceasta este înălțimea piramidei. Desenăm o perpendiculare atât de lungă încât muchia laterală să nu acopere imaginea de înălțime.
Figura unei piramide cvadrangulare regulate
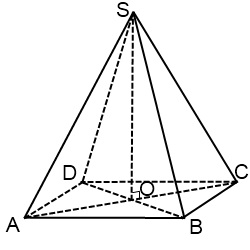
Figura piramidei drept patrulaterale începe, de asemenea, din partea de jos. Deoarece paralelismul segmentelor este păstrat, iar unghiurile nu sunt, pătratul din bază este reprezentat de o paralelogramă. Este de dorit ca unghiul ascuțit al acestei paralelograme să fie micșorat, apoi fețele laterale sunt obținute mai mult. Centrul pătratului este punctul de intersecție a diagonalelor sale. Desenează diagonale, din punctul de intersecție restabilim perpendicularul. Perpendicularul este înălțimea piramidei. Alegem lungimea perpendiculară astfel încât marginile laterale să nu se îmbine între ele.
Figura unei piramide hexagonale obișnuite
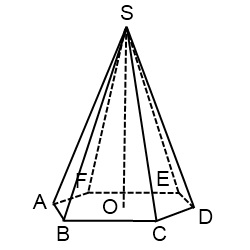
Deoarece proiectarea paralelă de segmente paralele sunt stocate, baza regulate piramida hexagonala - un hexagon regulat - descrie un hexagon, care laturile opuse sunt paralele și egale. Centrul hexagonului normal este punctul de intersecție al diagonalelor acestuia. Pentru a nu deranja desenul, nu tragem diagonalele, dar găsim acest punct aproximativ. Restaurarea perpendicular din aceasta - înălțimea piramidei - astfel încât marginile laterale nu sunt topite împreună.
Când construiți "secțiunea de aur", luați în considerare valoarea primară egală cu 7, 23 cm. Apoi, calculați coeficientul "secțiunii de aur". Acest număr este utilizat în diferite științe și este egal cu 1,618. Înmulțiți 72,3 mm cu 1,618, ceea ce este de 116,981 mm. Valoarea poate fi rotunjită - 117 mm, va fi egală cu laturile bazei piramidei. Deci - 7,2 cm - înălțimea piramidei, 11,7 cm - laturile bazei piramidei.
Acum conta dimensiunea fețe triunghiulare, folosind „legea lui Pitagora“ va primi 92.769 cm, rotunji valoarea la 9.3 cm. Ia un creion, riglă și hârtie, trage patru triunghiuri cu parametrii 11.7 * 9.3. Dacă piramida are o bază, atunci aveți nevoie și de un pătrat cu fețe 11,7 * 11,7 * 11,7 * 11,7. Pentru a prinde laturile piramidei, nu folosiți cuie și șuruburi - energia unei astfel de piramide va fi ruptă.
Așezați triunghiurile în așa fel încât să se dezvolte o piramidă și să se desfășoare la masă. Fixați marginile triunghiurilor cu bandă adezivă, bandă autoadezivă sau lipiți-le cu bucăți de hârtie lipite.
Aliniați punctele de colț ale primei și celei de-a patra fețe cât mai exact posibil. Întoarce-te. lipiți cusăturile interne. Verificați dimensiunea pătratului bazei. Puneți deoparte triunghiurile lipite, lăsați clema să se fixeze.
Modelul rezultat al piramidei este gol. Dacă este suficient, puteți lăsa piramida în această formă, dacă nu, lipiți cupola la bază. Direcționați această sursă de energie pozitivă pentru a rezolva anumite probleme.
Setați programul folosind anumite informații. Pictați piramida în culoarea dvs. preferată, lipiți poze, desenați modele, scrieți urări de bine. Utilizați-l ca o sursă de putere, marcați-i fețele pe fețe. Umpleți paharul cu apă, acoperiți-l cu cupola piramidei. Apa își va schimba proprietățile și va deveni una "vie".
Autosugestia sau nu, principalul lucru este credința în informație, iar gândurile bune se materializează neapărat.
Piramida (pyramid. Pyramid) -. una dintre fețele căreia (numită bază) este arbitrară. și celelalte fețe (numite fețe laterale). având un vârf comun. În funcție de numărul de colțuri ale bazei, piramidele sunt triunghiulare (), cvadrangulare etc. Piramida este un caz special.
Istoria dezvoltării piramidei în geometrie
Originea geometriei piramidei a fost pusă în Egiptul antic și în Babilon, dar a fost dezvoltată activ în Grecia antică. Volumul piramidei era cunoscut de vechii egipteni. Primul matematician grec care a stabilit ce era egal cu volumul piramidei a fost. dar sa dovedit. Matematicianul grec vechi a sistematizat cunoașterea piramidei în cel de-al 12-lea volum al său. și a derivat și prima definiție a piramidei: o figură solidă legată de planuri care converg dintr-un plan într-un punct (Cartea XI, definiția 12).
Elemente ale piramidei
SO - înălțime
SF - apophema
OF este raza cercului înscris în bază
- - înălțimea feței laterale a piramidei obișnuite, trasată de la vârf;
- laterale - triunghiurile convergente la vârf;
- margini laterale sunt fețe comune ale fețelor laterale;
- partea superioară a piramidei este un punct care leagă marginile laterale și nu se află în planul bazei;
- înălțime - o secțiune a perpendicularului trasată prin vârful piramidei în planul bazei sale (capetele acestui segment sunt vârful piramidei și baza perpendiculară);
- secțiunea diagonală a piramidei este secțiunea piramidei care trece prin vârful și diagonala bazei;
- baza este un poligon care nu face parte din partea de sus a piramidei.
Dezvoltarea piramidei
Dezvoltarea unei piramide regulate pentagonale:
1. în planul bazei ("stea")
2. în planul uneia dintre fețele laterale
Se numește matura plan figura obținută prin combinarea suprafeței geometrice a corpului cu un plan (fără impunerea unor fațete sau a altor elemente de suprafață între ele). Începând să studieze dezvoltarea suprafeței, aceasta din urmă este considerată în mod oportun ca un film flexibil, inextensibil. Unele dintre suprafețele reprezentate în acest fel pot fi aliniate cu planul prin îndoire. În acest caz, dacă suprafața compartimentului poate fi combinat cu un avion fără ruperea și lipire, suprafața unui astfel de apel construibil, iar forma plană rezultată - matura sale.
Proprietățile piramidei
Dacă toate marginile laterale sunt egale. atunci:
- în jurul bazei piramidei, puteți descrie un cerc, iar vârful piramidei este proiectat în centrul său;
- nervurile laterale formează unghiuri egale cu planul de bază;
- Reversul este valabil, de exemplu, dacă muchiile laterale pentru a forma un plan de bază unghiuri egale, sau dacă este aproape de baza piramidei poate fi descrisă ca un cerc, cu vârful piramidei este proiectată în centrul ei, toate marginile laterale ale piramidei sunt egale.
Dacă fețele laterale sunt înclinate la un unghi în planul bazei. atunci:
- în baza piramidei, puteți introduce un cerc, iar vârful piramidei este proiectat în centrul său;
- înălțimile fețelor laterale sunt egale;
- Suprafața laterală este egală cu jumătate din produsul bazei pe fața laterală.
Teoremele care leagă piramida cu alte corpuri geometrice
Descrierea sferei din jurul piramidei drepte:
SD - înălțimea piramidei.
AD este raza circumferinței care descrie baza.
B - mijlocul marginii marginii laterale
C este punctul de intersecție al avioanelor care trec prin mijlocul muchiilor perpendiculare pe ele.
AC = CS este raza sferei care descrie piramida
Sfera este înscrisă în piramida corectă:
D - centrul bazei
SF - apophema
ASD - planul bisector al unghiului dintre fețele laterale
BCE este planul bisector al unghiului dintre bază și fața laterală
C este punctul de intersecție al tuturor planurilor bisector
CK = CD este raza sferei înscrise în piramidă
- lângă piramidă, puteți descrie sfera atunci când există un poligon în partea de jos a piramidei, în jurul căruia puteți descrie un cerc (o condiție necesară și suficientă). Centrul sferei va fi punctul de intersecție a planurilor care trec prin mijlocul marginilor piramidei perpendiculare pe ele. Din această teoremă rezultă că ambele în apropierea oricărei piramide triunghiulare și apropiate pot descrie o sferă;
- În piramida, puteți introduce sfera atunci când piramidele interne se intersectează la un punct (). Acest punct va fi centrul sferei.
- Conul este numit inscripționat în piramida, dacă vârful lor coincide și baza sa este înscrisă în baza piramidei. În plus, conul poate fi înscris în piramidă numai atunci când apofemele piramidei sunt egale (o condiție necesară și suficientă);
- Conul se numește descris în apropierea piramidei, când vârfurile coincid și baza sa este descrisă aproape de baza piramidei. Și puteți descrie conul lângă piramidă numai atunci când toate marginile laterale ale piramidei sunt egale (o condiție necesară și suficientă);
- Înălțimile acestor conuri și piramide sunt egale una cu cealaltă.
- Cilindrul înscris într-o piramidă numită dacă una dintre bazei sale coincide cu cercul înscris în secțiunea transversală a piramidei cu un plan paralel cu baza și o altă bază aparține baza piramidei.
- Un cilindru se numește descris în apropierea piramidei, dacă partea superioară a piramidei aparține unei singure baze, iar cealaltă bază este descrisă aproape de baza piramidei. Și puteți descrie cilindrul din apropierea piramidei numai atunci când poligonul inscripționat (starea necesară și suficientă) este în partea de jos a piramidei.
Formule asociate cu piramida
- Piramida poate fi calculată prin formula:
,> unde V p> este volumul paralelipipedului;
- De asemenea, volumul unei piramide triunghiulare (tetraedru) poate fi calculat prin formula:
- Suprafața laterală este suma zonelor fețelor laterale:
- Suprafața totală este suma suprafeței laterale și a bazei:
- Pentru a găsi suprafața laterală a piramidei drepte, se pot folosi formulele:
Cazuri speciale ale piramidei
Piramida dreaptă
Piramida este numită corectă dacă aceasta este fundația. iar vârful este proiectat în centrul bazei. Apoi are următoarele proprietăți:
- marginile laterale ale piramidei obișnuite sunt egale;
- în piramida dreaptă, toate fețele laterale sunt triunghiuri isosceles;
- în orice piramidă corectă este posibilă atât înscrierea, cât și descrierea unei sfere în jurul ei;
- dacă centrele sferei înscrise și descrise coincid, atunci suma unghiurilor plane la vârful piramidei este π. și fiecare dintre ei, respectiv, π n >>. unde n este numărul laturilor poligonului de bază;
- aria suprafeței laterale a piramidei obișnuite este egală cu jumătate din produsul bazei pe apophema.
Piramida dreptunghiulară
O piramidă se numește dreptunghiulară dacă una dintre marginile laterale ale piramidei este perpendiculară pe bază. În acest caz, această margine este înălțimea piramidei.
Un tetraedru este o piramidă triunghiulară. Într-un tetraedru, oricare dintre fețe poate fi luată ca bază a piramidei. În plus, există o mare diferență între conceptele de "piramidă triunghiulară regulată" și "". Piramida dreaptă triunghiulară este o piramidă cu triunghiul drept în bază (fețele trebuie să fie triunghiuri isoscel). Un tetraedru este un tetraedru obișnuit, în care toate fețele sunt triunghiuri echilaterale.