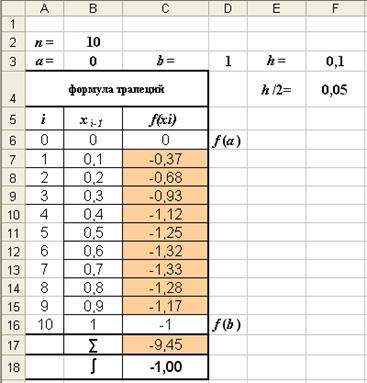
Aceste subintervale sunt construite dreptunghiuri, înălțimea lor este determinată de valoarea funcției f (x), în orice punct subinterval.
(. Figura 2.1) Dacă f (xi) este determinată de marginea stângă a fiecărei sub-fantă, atunci formula dreptunghi este după cum urmează:
și se numește formula dreptunghiurilor stângi.
Dacă f (xi) este definită pentru limita dreaptă a fiecărui subinterval (Figura 2), atunci
și se numește formula dreptunghiurilor drepte.
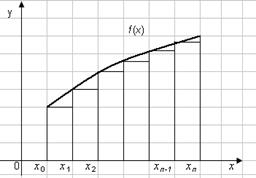
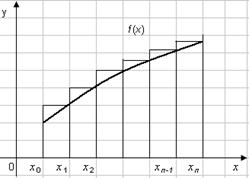
Dacă funcția este monotonică în intervalul [a. b], atunci într-un caz se obține valoarea integrală I cu o deficiență I1. iar în cealaltă - cu un exces de I2. O valoare mai precisă a lui I se obține prin medierea cantităților:
Dacă f (xi) este definită pentru mijlocul fiecărui subinterval, atunci formula dreptunghiului are următoarea formă:
și se numește formula dreptunghiurilor mijlocii.
Precizia integrării pentru aceste metode este aproximativ egală cu # 949; ≈ h.
Folosind formulele dreptunghiurilor stânga, dreaptă și mijlocie, calculează. dacă h = 0,2.
○ Calculați integralele folosind metoda dreptunghiului din tabelul Excel (fig.3, 3-a).
Valorile intervalului de integrare [0, 1] sunt plasate, respectiv, în celulele B3 și F3. Intervalul de integrare este împărțit în 5 subintervențe (n = 5). Introduceți valoarea lui n în celula B2. Pasul de integrare este calculat în celula F2 prin formula
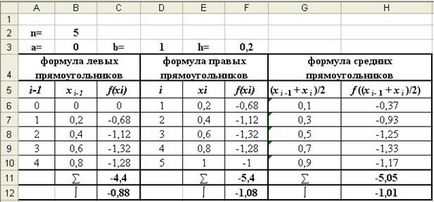
Fig. 3 (Mod soluție)
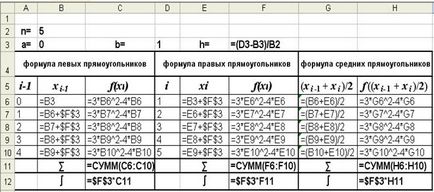
Formula de afișare a modului
I) Pentru calcularea aproximativă a integrității prin formula dreptunghiurilor stângi (3), este necesar să se calculeze valorile funcției f (x) = 3x 2 - 4x la punctele (2):
Calcularea valorilor lui x0. x1. x2. x3. x4. este reprezentat în blocul de celule B6: B10, iar valorile funcției corespunzătoare sunt în blocul de celule C6: C10.
Apoi, calculați suma acestora (în celula C11) și multiplicați valoarea rezultată prin etapa de integrare h (în celula C12):
Σ = 0-0,68-1,12-1,32-1,28 = -4,4 I = 0,2 # 8729; (-0,44) = -0,88.
II) Pentru calcularea aproximativă a integrității prin formula dreptunghiurilor drepte (4) este necesar să se calculeze valorile funcției f (x) = 3x 2 - 4x în punctele:
Calculul valorilor lui x1. x2. x3. x4. x5 este reprezentat în blocul de celule E6: E10, iar valorile funcției corespunzătoare sunt în blocul de celule F6: F10.
Apoi, calculați suma lor (în celula F11) și multiplicați rezultatul prin etapa de integrare h (în celula F12):
Valoarea aproximativă a integrala, calculată prin formula dreptunghiurilor stângi, este de -0,88, iar formulei dreptunghiurilor drepte este -1,08.
Valoarea lor medie este mai apropiată de o valoare exactă egală cu -1.
III) Pentru calcularea aproximată a integralului folosind formula dreptunghiurilor medii (5), este necesar să se calculeze valorile funcției f (x) = 3x 2 - 4x în punctele:
(xi-1 + xi) / 2 (blocul de celule G6: H12), suma lor (celula H11), multiplica valoarea rezultată prin etapa de integrare h (celula H12).
Prin divizarea intervalului de integrare într-un număr mai mare de segmente, de exemplu, cu 10, puteți obține o soluție mai precisă (Figura 4).

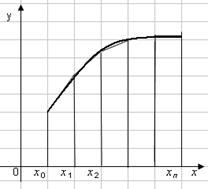
Deoarece suprafața trapezului este egală cu jumătate din suma bazelor înmulțită cu înălțimea, integramentul este aproximativ egal cu suma zonelor tuturor trapezelor obținute:
Astfel, formula trapezoidală are forma:
I = ≈. (8)
Precizia integrării pentru această metodă este aproximativ egală cu # 949; ≈ h 2.
Exemplu (continuare). Folosind formula trapezoidală, se calculează pentru h = 0,2.
Soluția. Calcularea metodei integrale prin trapez (8) este fezabilă în tabelul Excel (fig.6, 6-a).
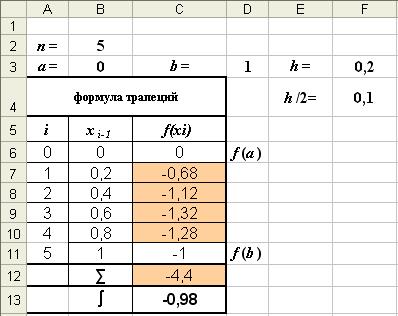
Σ = -0,68 -1,12 -1,32 -1,28 = -4,4 I = 0,1 · [(0-1) -2,4,4] = -0,98
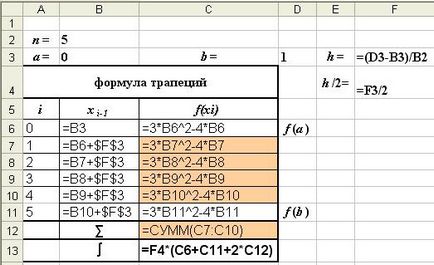
Formula de afișare a modului
Prin divizarea intervalului de integrare într-un număr mai mare de segmente, de exemplu cu 10, putem obține o soluție mai precisă (figura 7).