Să ne întoarcem la modelul sistemului mecanic dat în exemplul 3.1. Ecuația modelului nelinar are forma
.
Din ecuația de ordinul doi se poate ajunge la un sistem autonom al formei
,
Dacă acum excludem timpul t în sistem, obținem ecuația diferențială a traiectoriilor sistemului pe planul de fază
Ultima ecuație poate fi rescrisă după cum urmează:
Apoi, presupunând că pentru, a. După integrarea ecuației în intervalul de la, obținem egalitatea
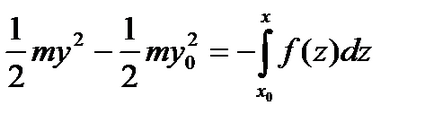
care pot fi rescrise ca:
Observăm asta
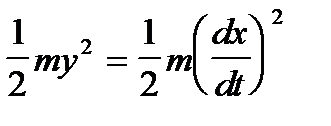
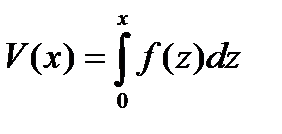
- formula energiei sale potențiale. Astfel, ecuația exprimă legea conservării energiei:
unde este energia totală a sistemului.
Este clar că ultima ecuație este ecuația traiectoriilor de fază ale unui sistem conservator neliniar, deoarece este obținută ca urmare a integrării ecuației
Astfel, curbele diferite ale energiei constante corespund diferitelor valori ale lui E în planul de fază. Punctele staționare ale sistemului sunt punctele M * (x *, 0), unde x * reprezintă rădăcinile ecuației. În acest caz, dacă rescriem ecuația legii conservării energiei în formă
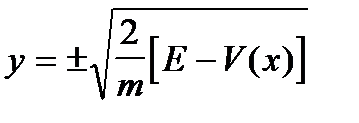
atunci este ușor să construim traiectorii de fază.
Argumentele generale de mai sus ne permit să studiem ecuația de mișcare a unui pendul într-un mediu fără rezistență, care are forma
. unde este o constantă pozitivă.
Deoarece ecuația este un caz particular al ecuației. atunci ea poate fi interpretată și ca o ecuație care descrie mișcarea rectilinie fără frecare a unui corp de masă unitate sub acțiunea unui arc neliniar, unde forța de refacere este egală cu. În acest caz, sistemul autonom corespunzător ecuației va fi scris în formă
Punctele singulare de aici sunt a și ecuația diferențială a traiectoriilor de fază ale sistemului ia forma
Separând variabilele din ultima ecuație și integrând, obținem ecuația de traiectorii de fază
Ultima ecuație este un caz special al ecuației legii conservării energiei, unde. și energia potențială este dată de
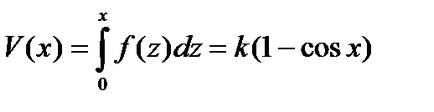
După stabilirea valorilor. putem schița schematic o imagine a comportamentului traiectoriilor în planul de fază, dacă folosim relația.
Portretul de fază care rezultă arată (vezi Figura 3.3) că dacă energia se schimbă de la la. traiectoriile de fază corespunzătoare sunt închise, iar ecuația are soluții periodice. Pe de altă parte, dacă. traiectoriile de fază corespunzătoare nu sunt închise, iar ecuația are soluții periodice. Valoarea în planul fazelor corespunde traiectoriei fazei, care separă cele două tipuri diferite de mișcare, o astfel de traiectorie este numită separatrix. traiectorii de fază de ondulare situată în afara separatrices corespund mișcării de rotație a unui pendul și trasee situate în zonele delimitate de separatrices închis - propunerea vibraționale.
Fig. 3.3. Faza portret a unui sistem conservator neliniar
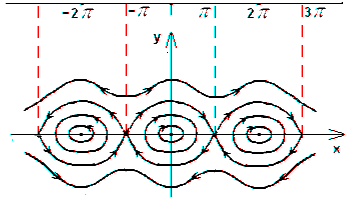
Figura 3.3 arată că în vecinătatea punctelor fixe. unde comportamentul traiectoriilor de fază diferă de comportamentul traiectoriilor de fază în vecinătatea punctelor fixe. unde
Să vedem acum modul în care fricțiunea liniară afectează comportamentul traiectoriilor de fază ale unui sistem conservator. În acest caz, ecuația ia forma
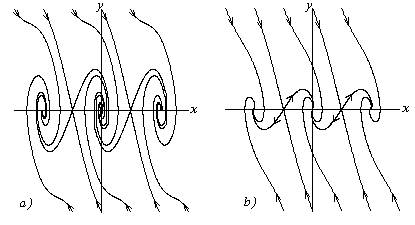
Fig. 3.4.Photratele Phase ale sistemelor conservatoare cu frecare
Un astfel de sistem va fi neconservativ. Dacă frecare în el este suficient de mică, adică este posibil să se arate că traiectoriile de fază sunt prezentate schematic în figura 3.4, a. Dacă fricțiunea nu permite nici o oscilație a pendulului față de poziția de echilibru, atunci imaginea traiectoriilor de fază va avea forma prezentată în Fig. 3.4, b.
Dacă vom compara acum portretul de fază a unui sistem conservator cu ultimele două portrete de fază de sisteme non-conservatoare, se poate observa că traiectoriile de fază închise în frecare redusă, mutat într-o spirală, și cu o frecare puternică - în calea care fac parte din punctele singulare în anumite direcții.
Fig. 3.4.Photretele de fază ale sistemelor cu frecare: a - frecare mică; b - frecarea ridicată