1.4 Diagrame 4. Proiecții ale unei găuri străpunse într-o sferă
Un exemplu. În desenul cu trei proiecții, construiți proiecțiile lipsă ale orificiului periferic în sfera unei raze date
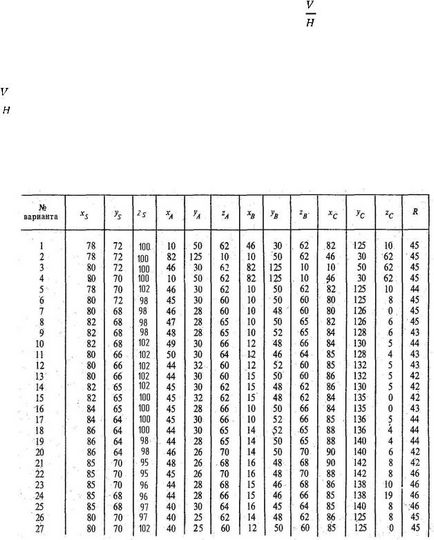
Datele pentru varianta lor sunt date în tabelul 4. Un exemplu de diagramă este prezentat în figura 9.
Linii directoare pentru rezolvarea problemei
Din valorile numerice ale coordonatelor centrului O al sferei preluate din tabelul 4, în funcție de numărul variantei problemei, sunt construite proiecțiile sale (o.o ', o "). Radius R efectuează trei proiecții ale sferei.
Apoi, proiecțiile frontale a, b ', c' și d 'ale vârfurilor patrulaterale sunt construite. Împerecherea prin conectarea proiecțiilor liniei drepte ale punctelor, proiecția frontală a orificiului intermediar din sferă - un poligon reprezentând proiecția degenerată a liniei prin gaură - este obținută în desen. O astfel de proiecție degenerată a găurii din sferă se obține numai în cazul intersecției sale cu patru planuri (compartimente) proiectate în față. În intersecția compartimentelor adiacente ale planurilor proeminente, marginile AA 1. BB 1. CC 1. DD 1 ale tetraedrului sunt formate.
Se știe că sfera este intersectată de un plan de-a lungul circumferinței. Prin urmare, linia de intersecție a sferei cu tetraedrul este compartimentele cercurilor conectate prin punctele de intersecție a marginilor cu sfera.
În funcție de locația secantului
să construiască proiecțiile punctelor de intersecție a fiecărui margine al tetraedrului cu sfera și proiecția compartimentelor cercurilor de intersecție a sferei cu fiecare dintre cele patru fețe.
Fața AA 1 BB 1 este zona de proiecție frontală. Acesta este amplasat oblic față de planurile orizontale și de profil ale proiecțiilor. Circumferința secțiunii sferei de către acest plan este proiectată pe ele sub forma unei elipse. elipsă de construcții produc proiecții de puncte, prelevate pe compartimentul circumferința secțiunii frontală proiecție sferă care coincide cu partea din față a „“ 1, b „b“ fețele 1 proiecție. O multitudine de puncte de pe circumferință separate în poziția tragere a caracteristicii de proiecție frontală (referință) puncte de restricționare mari (punctul 5“, 5' 1) și mici (punctul 1«și 1 1) axele elipsei, situate la ecuator (punctele 3»și 3 "1. Puncte de vizibilitate pentru planul orizontal al proeminențelor, punctele 2 și 2 fiind puncte de vizibilitate pentru planul profilului proiecțiilor)
și principalele meridiane, precum și câteva puncte arbitrare. De exemplu, pentru a construi un punct 4 (4 și 4 ') este necesar să se traseze o paralelă prin punctul 4'. Pe planul orizontal al proiecțiilor, paralela este proiectată într-un cerc cu raza r 4. Punctul 4 va aparține acestei linii.
Proeminențele orizontale și profilate ale punctelor selectate pe planul frontal al proeminențelor sunt construite pe baza apariției ultimei suprafețe sferice. În acest caz, trebuie să procedăm din faptul că proiecția unui punct care aparține unei suprafețe sferice ar trebui să fie localizată pe proiecțiile corespunzătoare ale paralelului sau meridianului său.
Fațetele 1 BB CC DD 1 1 și AA 1 sunt planuri orizontale nivelul compartimentelor. Compartimentele formele lor secționate - cerc, proiectate pe un plan orizontal de proiecție în dimensiunea reală a razei r b și r d este paralela cu raza plane coincidente nivel orizontal. În același timp, determină poziția orizontală proiecții BB 1. CC 1. puncte DD 1 margini de intersecție cu sfera - un punct b. b 1. c. c 1. d. d 1. În conformitate cu punctele de vedere din față și planul secțiuni de coaste și compartimentele de linii de a construi proiecția lor profil.
Fața SS 1 DD 1 este compartimentul planului profilului nivelului. Caseta de cerc situată în această față este proiectată pe planul profilului proeminențelor în dimensiune completă. Raza secțiunii cercului r din secțiune este egală cu raza meridianului, care coincide cu planul profilului nivelului feței.
Schița finală a orificiilor prin gaură din sferă este realizată ținând seama de vizibilitatea proeminențelor lor în desen. Vizibilitatea proiecțiilor punctelor și liniilor sferei este determinată de localizarea acesteia din urmă față de ecuator sau de principalele meridiane. Proiecțiile vizibile ale liniilor sunt realizate printr-o linie continuă groasă, iar liniile invizibile sunt întrerupte.
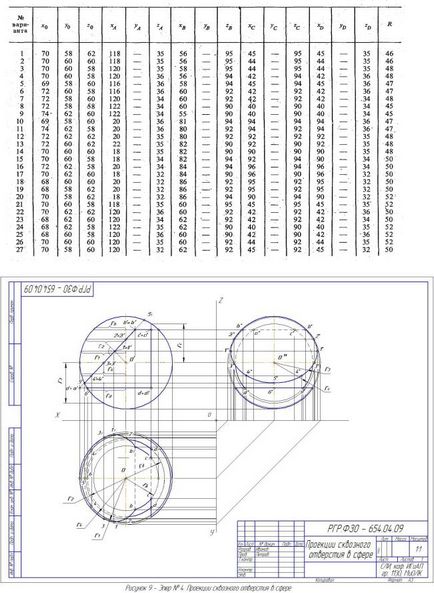
Tabelul 4 - Date pentru diagrama nr. 4 Dimensiuni în milimetri
1.5 Diagrama 5. Secțiunea unui con cu un plan de poziție generală
Un exemplu. Construiți proiecțiile liniei de intersecție a unui con rotund circular de rotație cu un plan de poziție generală. Construiți valoarea reală a secțiunii transversale.
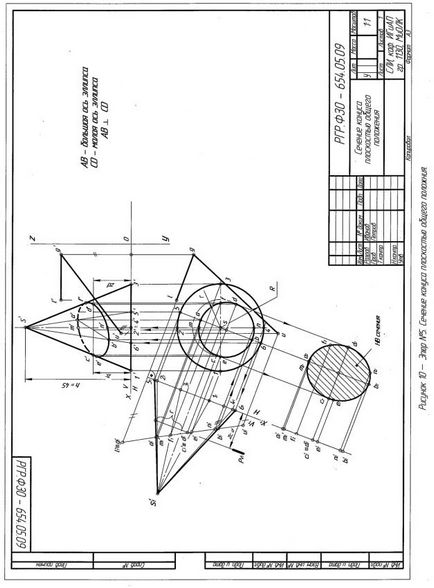
Datele pentru varianta lor sunt date în Tabelul 5. Un exemplu de diagramă este prezentat în Figura 10.
Instrucțiuni pentru rezolvarea diagramei. Pe formatul A3, coordonați axele
și din tabelul 5, în funcție de versiunea lor, se iau valorile (coordonatele lui X.Y. Z), care definesc suprafața conului de rotație și a planului secant. Se determină centrul cercului cu raza R a bazei conului, punctul S (s, s '). Conul se află pe planul H. Înălțimea conului h este numeric
este egală cu coordonatul Z S. Planul secant este determinat de coordonatele punctelor LGU.
Soluția diagramei. Planul unui corp geometric este numit figură plană, care conține puncte care apar atât la suprafață, cât și la planul secant. Principiul construirii unei secțiuni constă în determinarea punctelor de intersecție ale marginilor sau generatoarelor unei suprafețe date cu un plan secant.
Figura 10 prezintă construcția formei secțiunii unui con circular drept cu un plan de poziție generală dat de liniile intersectate LG
și GU. unde LG este orizontal.
Construcția este realizată folosind metoda de schimbare a planurilor de proiecții. Un plan de proiecție suplimentar V 1 este ales astfel încât să fie perpendicular nu numai pe planul H. ci și pe planul secant (LG x GU). Pentru aceasta, axa X 1 este perpendiculară pe proeminența orizontală a orizontalei planului secant lg - X 1 lg. În acest caz, planul secant este proiectat pe un plan V 1 sub forma unei linii. Deoarece planul de tăiere intersectează toate generatoarele conului, forma secțiunii va fi o elipsă, o vedere frontală coincide cu proiecția planului de tăiere - intervalul „1 b“ 1. Tăiați „1 b“ 1 este, de asemenea, proiecția frontală a axei majore și sale cantitate naturală. După cum știți, elipsa este construită pe două axe. o axă majoră și o axă minoră. Axa minoră este perpendiculară pe axa principală a elipsei. Divizarea intervalul 1 jumătate „1 b“ găsi un punct care este o vedere frontală a axei mici a elipsei (c „1 ≡ d“ 1) și este centrul de proiecție al elipsei.
Prin punctul c '1 ≡ d' 1 tragem un plan auxiliar P || H. Acest plan va diseca conul de-a lungul unui cerc de rază r, care este proiectat pe planul H fără distorsiuni. După ce am tras-o, găsim punctele c și d. Determinarea dimensiunii reale a axei minore a elipsei.
Pentru a construi o proiecție orizontală și frontală a secțiunii în
punctele aparținând secțiunii transversale văzută din desen. De exemplu, formând un S (1 s. 1 's') și 3 S (3 s, 3 's') pot determina punctul E (e, e ') și F (f, f'), care sunt de sprijin și împărți vedere frontală forma a sectiunii transversale (elipsa) pe
partea vizibilă și invizibilă în sistemul de avioane. Desenul arată
săgeată, construcția punctului B (b. b ') aparținând generatorului 6 S. și construcția punctului N (n, n') aparținând generatorului 4 S.
Valoarea naturală a secțiunii transversale este determinată de metoda deplasării plane-paralele. Proiecția frontală a figurii secțiunii în sistemul de planuri
paralel cu planul H = a'b'c'd'e'f'm'n '|| H. Prin urmare, în planul H această cifră este proiectată în dimensiune completă.
Tabelul 5 - Date pentru diagrama nr. 5 Dimensiuni în milimetri
1.6 Diagrama 6. Intersecția unui con circular drept cu un cilindru de rotație
Un exemplu. Construiți o linie de intersecție a unui con circular drept cu un cilindru de rotație. Construiți cilindrii cilindrului de rotație intersectat cu un con circular drept.
Diagrama este executată pe două foi de hârtie de desen A4 și A3
Fila 1. Construcția unui desen ortogonal al liniei de intersecție a unui con circular drept cu un cilindru de rotație.
Instrucțiuni pentru diagramă. Pe foaia de format A3, axele de coordonate sunt trase și din tabelul 6, în funcție de varianta lor, ele iau valori care definesc suprafețele unui con circular drept și un cilindru de rotație.
Determinați centrul (punctul S) al circumferinței diametrului D. a bazei conului circular drept în planul orizontal al proeminențelor. Este construită o proiecție frontală a conului, înălțimea h fiind egală numeric cu coordonatul Z S.
Axa de rotație a cilindrului este frontal proeminent drepte. care trece prin punctul T (t, t „), bazele cilindrului sunt cercuri cu diametrul D 1. generatoarele cilindrului au o lungime egală cu 1,5 D 1 și împărțit în jumătate după planul meridian principal al unui con circular drept - linia I - V.
Analiza localizării figurilor geometrice date în raport cu
reciproc și planurile proiecțiilor:
- o suprafață cilindrică este o proeminență proeminentă în raport cu planul frontal;
- linia de intersecție a suprafețelor este o curbă spațială, ale cărei puncte aparțin ambelor suprafețe;
- Din moment ce suprafața cilindrică se extinde în față, este evident că, cu proeminența frontală a cilindrului - cercul situat în interiorul conturului triunghiului, proiecția frontală a intersecției suprafețelor date coincide;
- conturul unui triunghi este proiecția meridianului principal al unui con circular drept.
Pentru a construi o proiecție orizontală a curbei intersecției unui con cu un cilindru pe proiecția frontală, se disting pozițiile proeminențelor suportului și mai multe puncte arbitrare.
Pe planul frontal al proiecțiilor, pozițiile punctelor e 'și f' ale intersecției proiecției frontale a cilindrului cu meridianul principal al conului sunt marcate în primul rând. Aceste puncte se numără printre punctele de referință. Dintre acestea: punctul e este proiecția frontală a celei mai înalte și punctul f este punctul cel mai drept al curbei de intersecție a figurilor. Punctele a și a 1 sunt proiecții ale punctelor inferioare ale curbei
intersecție. Punctele c 'și c' sunt proiecții ale punctelor de vizibilitate ale proiecției orizontale a curbei de intersecție. Punctele b '. b 1 ', d' și d 1 'sunt proiecții ale punctelor arbitrare ale curbei. Poziția lor în desen este aleasă pentru confort pe axa de rotație a conului.
Astfel, proiecția frontală a liniei de intersecție
e'd'c'b'a'f'a '1 b' 1 c '1 d' 1 e 'coincide cu proiecția frontală a cilindrului de rotație, deoarece aceasta este suprafața proeminentă.
Soluția grafică ulterioară a problemei reduce la construirea proiecțiilor orizontale ale punctelor marcate ale curbei de intersecție a figurilor geometrice date.
Deoarece suprafața cilindrică este un front-proiecție, construcția proiecțiilor orizontale ale punctelor de intersecție a curbei este posibilă numai pe baza apartenenței lor la suprafața laterală a conului. Prin urmare, proiecțiile orizontale ale punctelor marcate ale curbei sunt construite folosind paralele ale unui con circular drept.
Pentru a face acest lucru, pe planul frontal al proiecțiilor din interiorul conturului triunghiului - principalul meridian al conului direct al rotației - paralelele sunt trase prin proiecțiile frontale corespunzătoare punctelor curbei. Marcați punctele de intersecție ale acestor linii cu una din laturile meridianului principal al conului.
Prin aceste puncte de linii de racordare se realizează până la intersecția cu orizontala principal trasa planul longitudinal al conului - linia I - V. soluție calibrată, egală cu distanța dintre aceste puncte la proiecția orizontală a axei de rotație a conului, este realizată raza Rb cercului. Rd. Rc sunt proiecțiile orizontale ale paralelelor punctelor corespunzătoare ale curbei de intersecție. În cele din urmă, prin proiecția frontală a punctului de b'b intersecția curbelor „1. c'c“ 1. d „1 selectată se realizează o linie de comunicație și punctul de intersecție cu puncte paralele de proiecție orizontală. Obțineți proiecții orizontale ale punctelor bb 1. cc 1. dd 1 a liniei de intersecție. Construcția punctelor aa 1. e. F poate fi văzută din desen.
Prin conectarea unei curbe netede cu ajutorul unei curbe, proiecțiile orizontale ale punctelor e, d, c, b, a, f, a 1. b 1. c 1. d 1. e. obținem o proiecție orizontală a curbei intersecției unui con circular drept cu un cilindru de rotație. În acest caz, proiecțiile vizibile ale punctelor curbei de intersecție sunt legate printr-o linie groasă solidă, iar proiecțiile invizibile printr-o linie punctată. La punctele cc 1, modificările de vizibilitate. După construirea unei proiecții orizontale a curbei de intersecție a suprafețelor de rotație, liniile finale ale desenului sunt desenate cu un creion. Liniile solide subțiri ale construcțiilor auxiliare, liniile de comunicare din desen ar trebui păstrate.
Toate denumirile digitale și alfabetice trebuie să se facă într-un font de desen.
Foaia 2. Construcția unei curse a unui con circular drept și a unui cilindru de rotație cu linia de intersecție aplicată acestora.