Să o α1 plan și ct2 ecuațiile lor generale. Apoi, unghiul φ dintre planurile și a1 a2 înseamnă cel mai mic unghiul la care este necesar să se transforme unul dintre planurile înainte de a se suprapune cu un alt plan. prin urmare
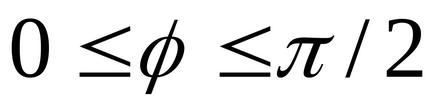
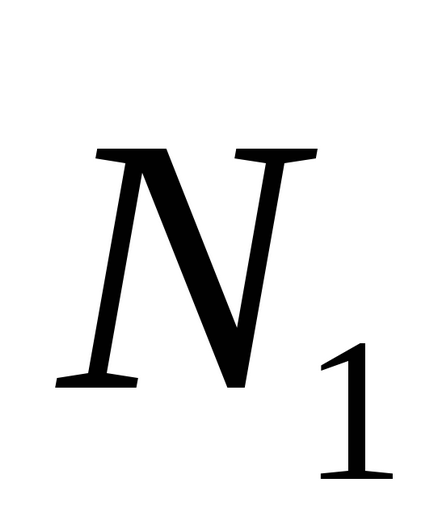
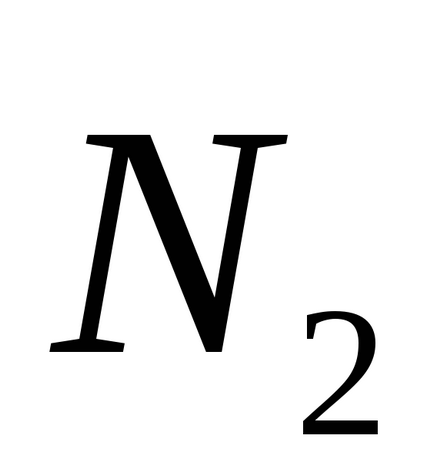
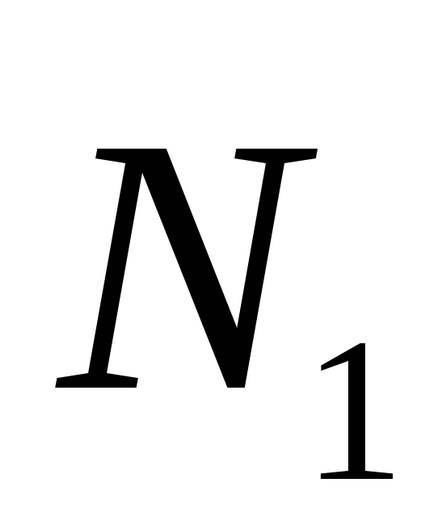
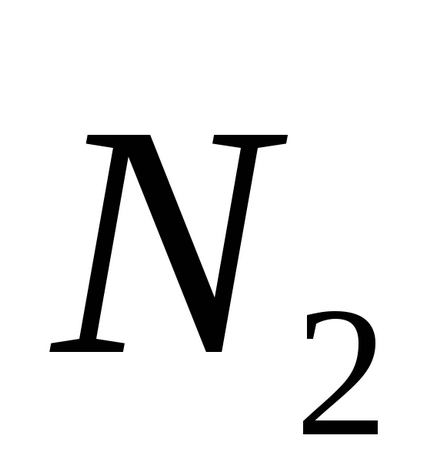
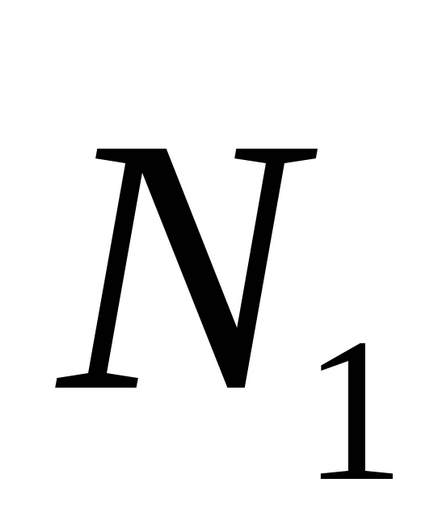
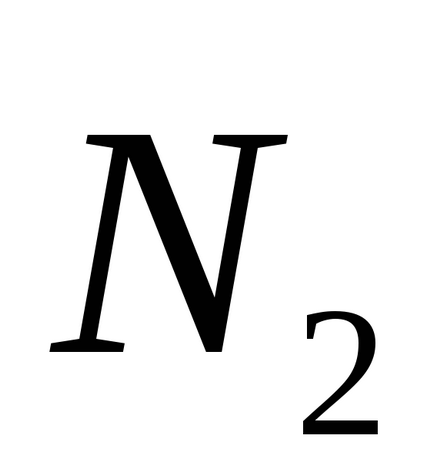
În special, dacă φ = π / 2, atunci
- starea de perpendicularitate a două planuri.
Direct în spațiu. Aranjamentul reciproc al unei linii drepte și al unui plan în spațiu Ecuația unei linii drepte în spațiu
Evident, o linie dreaptă în spațiu poate fi definită ca linia de intersecție a două planuri α1 și α2. Apoi, într-un sistem arbitrar de coordonate afine, linia dreaptă este dată de un sistem de două ecuații liniare
- ecuația generală a unei linii drepte sau ecuația unei linii drepte în formă generală.
Să fiu o linie. Apoi, poziția sa în spațiu este determinată în mod unic prin specificarea vectorului său de direcționare


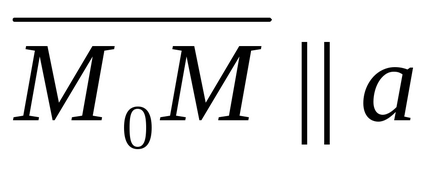
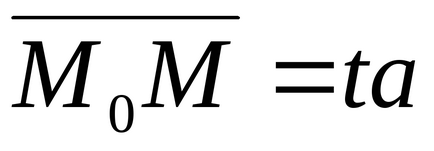
Trecând la coordonate, obținem
X - x0 = tm, y - y0 = tn, z - z0 = tp
-ecuația parametrică a unei linii drepte.
Exprimarea parametrului t. avem
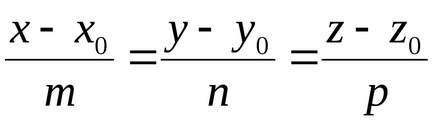
- Ecuația canonică a unei linii drepte care trece printr-un punct
M0 (x0y0, z0) este paralel cu vectorul

Ultima ecuație este echivalentă cu
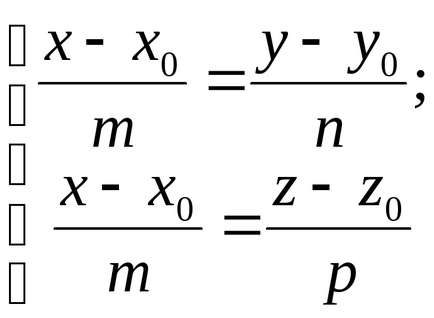
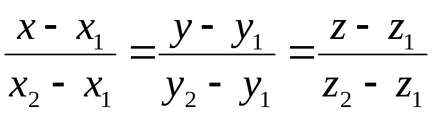
- ecuația unei linii drepte care trece prin două puncte date.
Dimpotrivă, lăsați ecuația generală a liniei.
Luând un punct arbitrar M0 (x0, y0, z0) al liniei, obținem
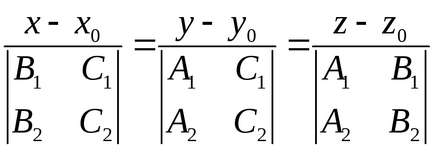
- ecuația canonică a unei linii drepte.
Aranjamentul reciproc de două linii în spațiu
Liniile l1 și l2 să fie date de ecuațiile canonice
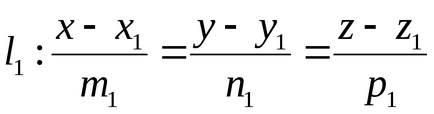
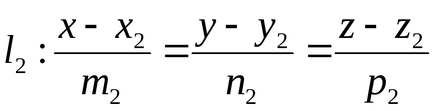
Semnificăm prin
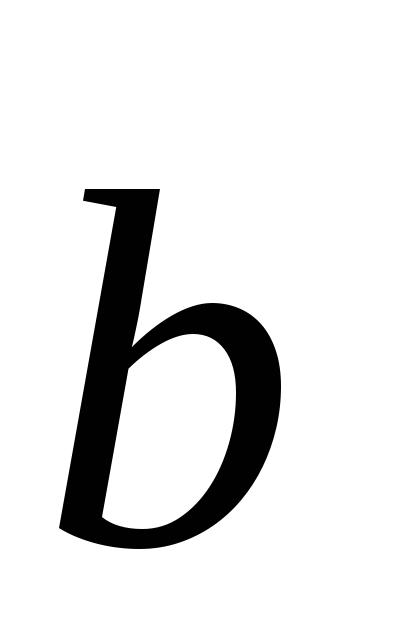
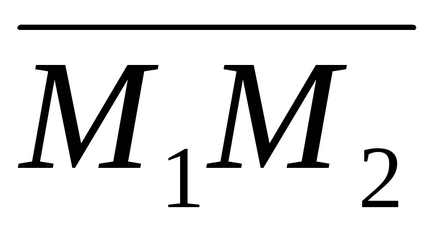
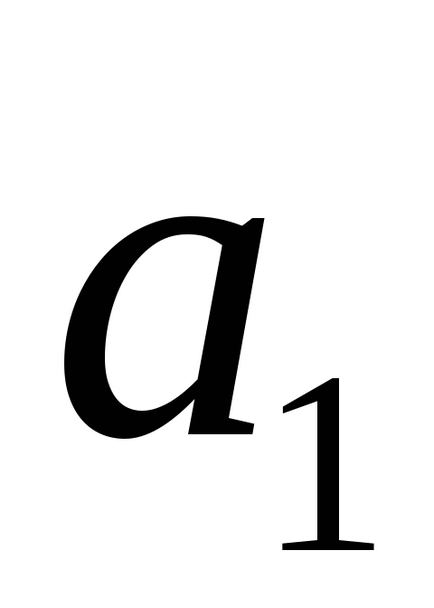
1) dacă liniile coincid, atunci toate cele trei vectori
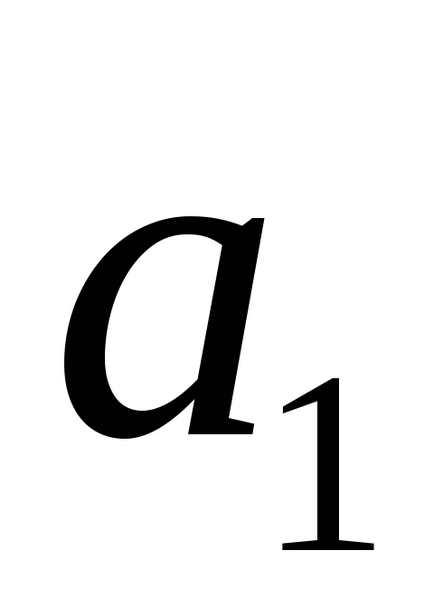
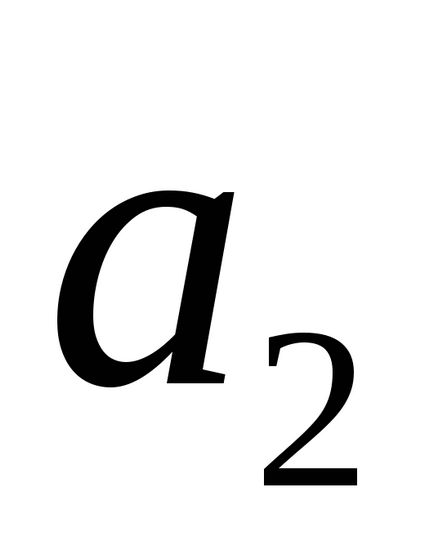
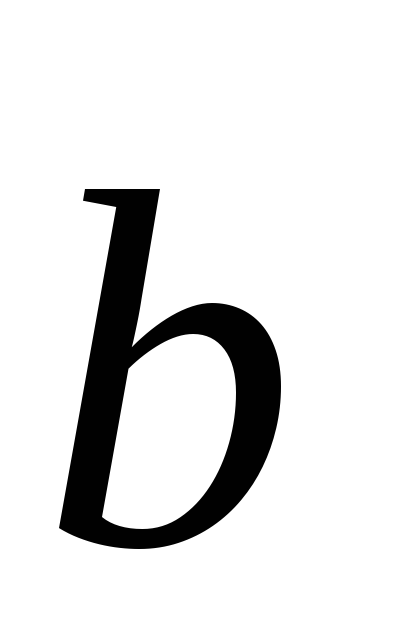
2) dacă liniile sunt paralele și nu coincid, atunci vectorii
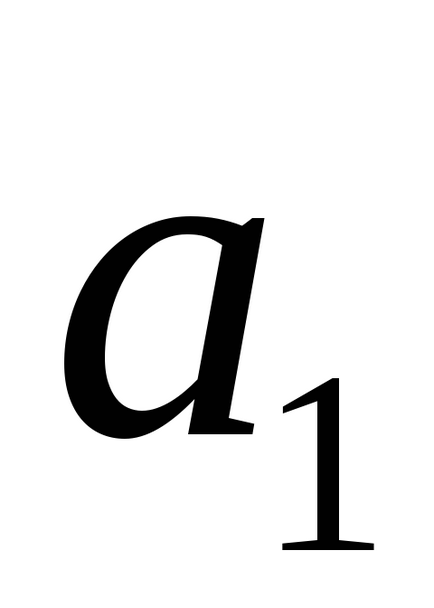
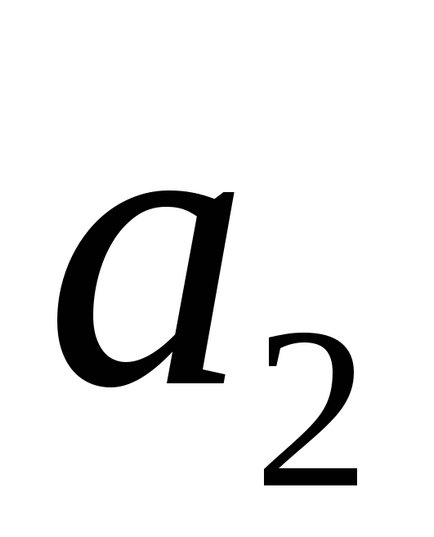
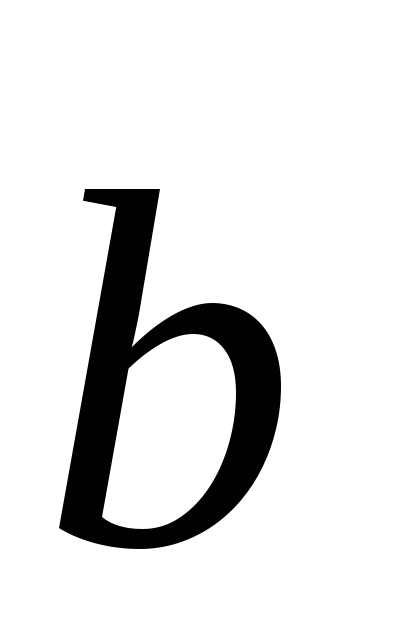
3) dacă firele se intersectează, atunci nu există două vectori
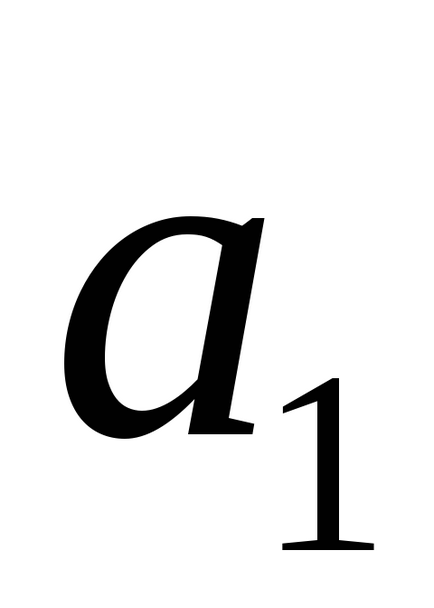
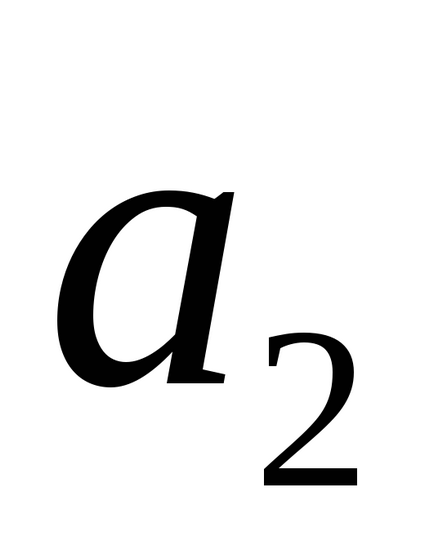
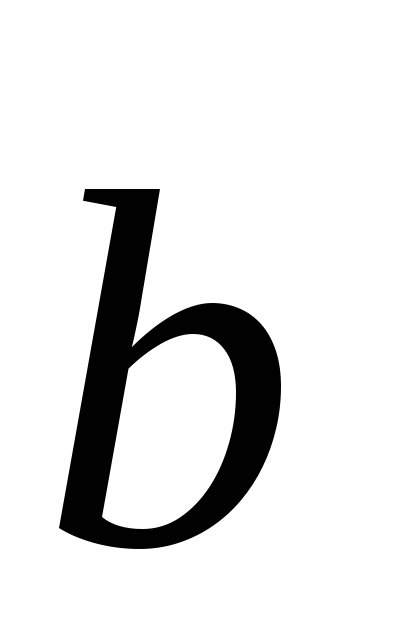
4) Dacă liniile drepte sunt încrucișate, atunci vectorii
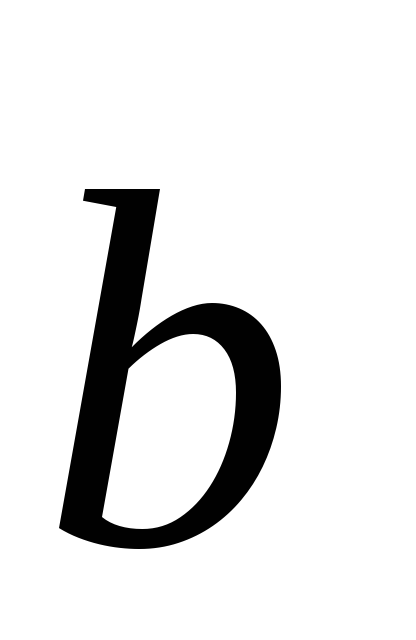
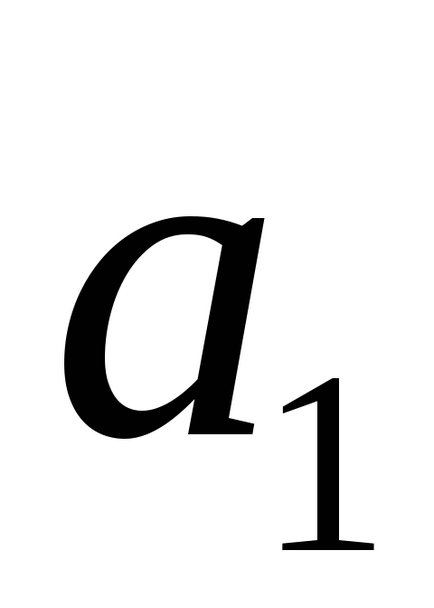
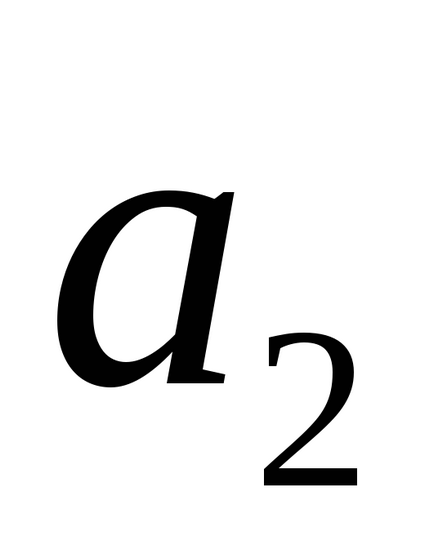
Rețineți că condițiile de paralele și perpendiculare, liniile drepte și l2 sunt l1 termeni echivalenți sunt coliniari și vectorii lor direcție ortogonale
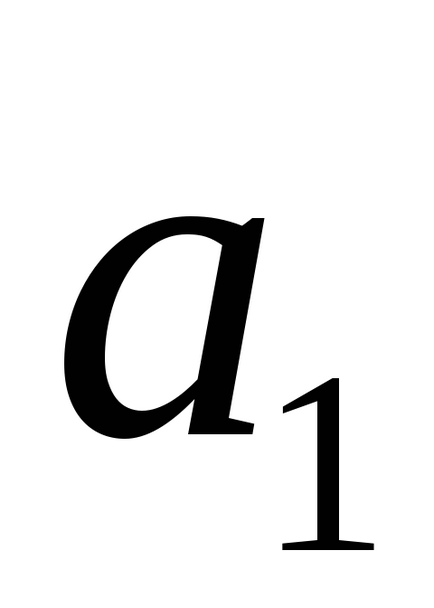
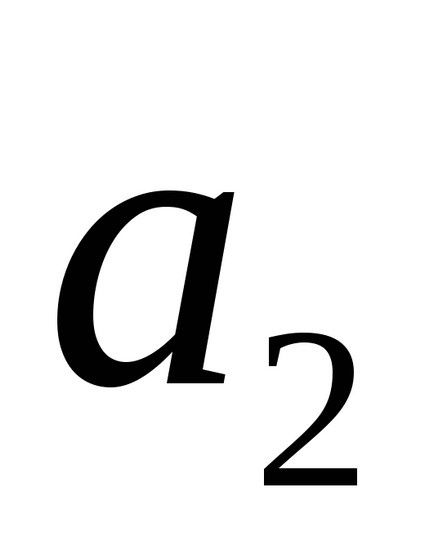
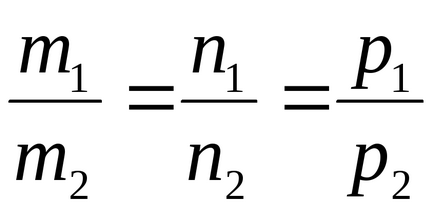
- condiții necesare și suficiente pentru paralelismul a două linii.
- condiții necesare și suficiente pentru perpendicularitatea a două linii.
Dacă liniile l1 și l2 se intersectează, atunci valoarea unghiului φ între ele este fie (
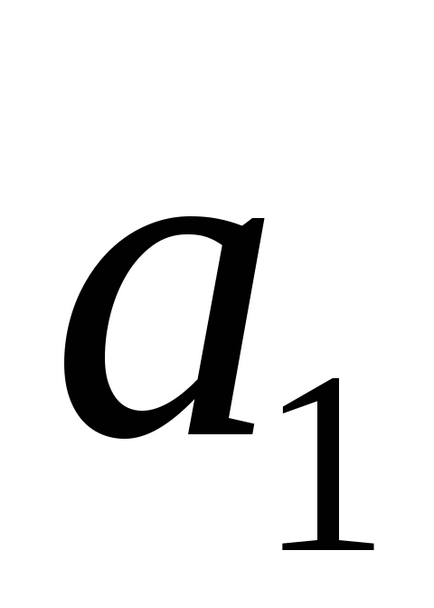
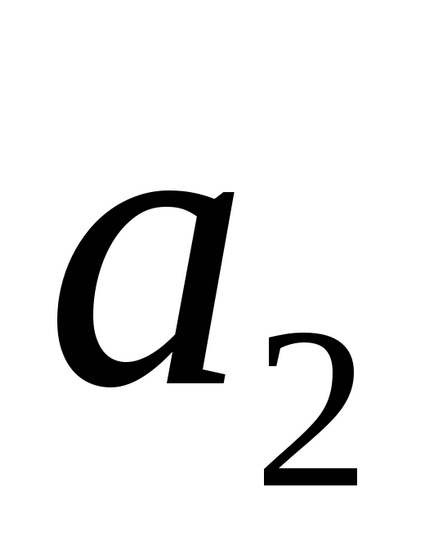
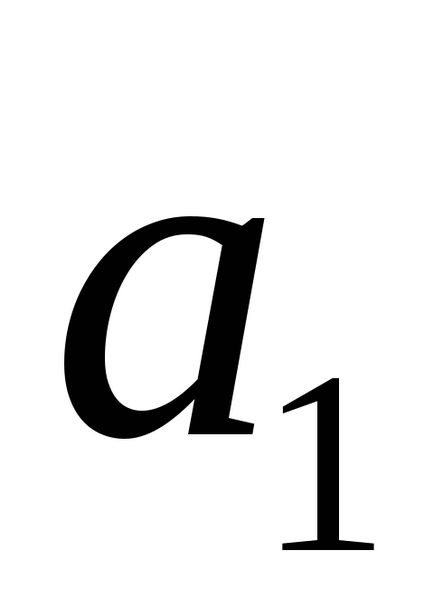
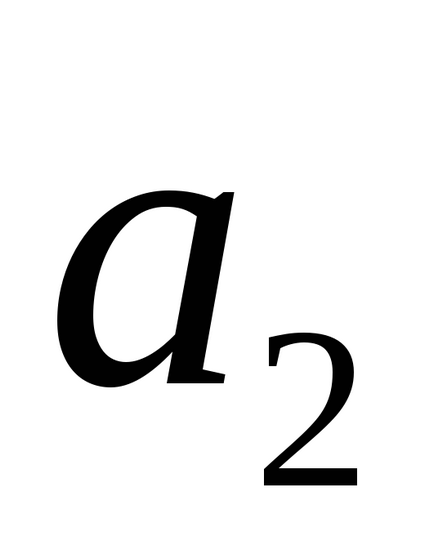
Distanta de la punct la linie in spatiu
Distanța d de la punctul M1 (x1, y1, z1) la o linie dreaptă dată
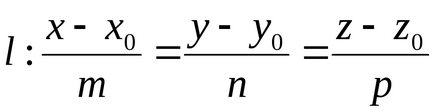

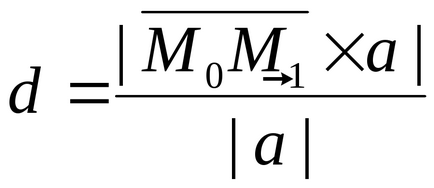
Ecuația unui plan care trece prin două linii date
Fie planul α să treacă prin liniile l1 și l2. date de ecuațiile următoare:
Indicăm prin M2 (x2, y2, z2),
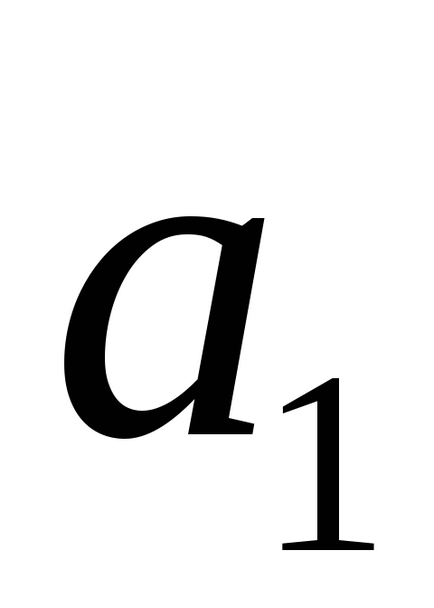
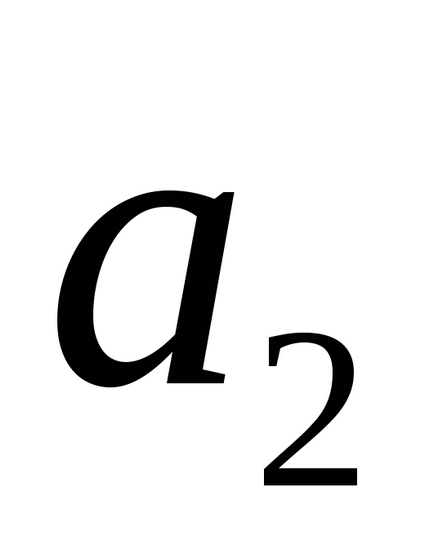
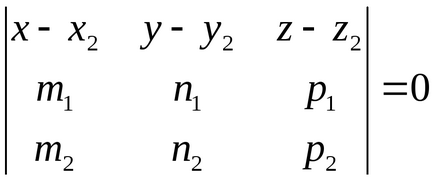
-ecuația unui plan care trece prin două linii drepte.
Distanța dintre liniile drepte încrucișate
Lăsați liniile l1 și l2. dată de ecuațiile (2) sunt oblic. Apoi distanța d între ele este lungimea perpendicularului trasată de la o linie dreaptă la cealaltă. Rețineți că distanța necesară este egală cu segmentul perpendicularului care este pivotat între planurile α1 și α2. unde α1 și α2 în același timp, planul paralel cu vectorii
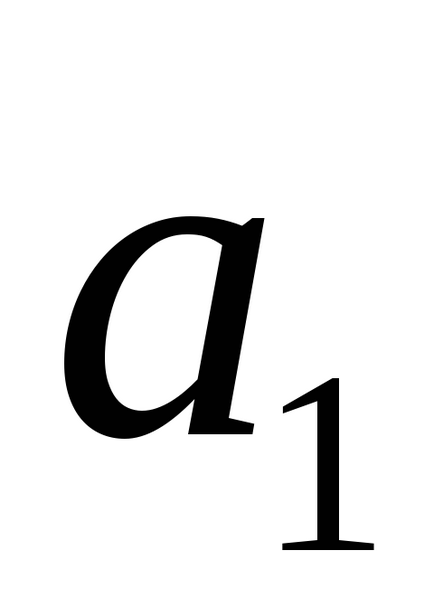
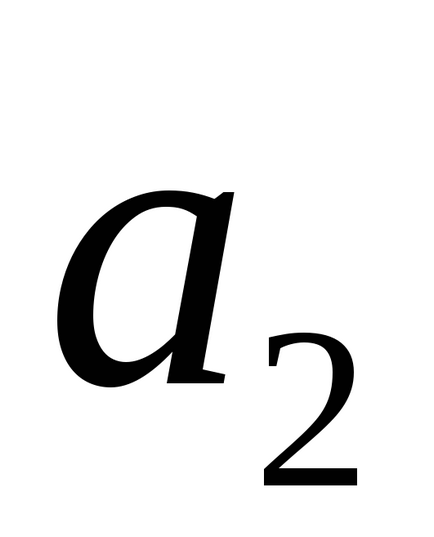
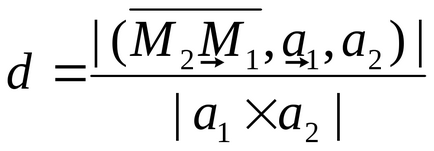
Aranjamentul reciproc al unei linii drepte și al unui plan
Să presupunem că linia l și planul α sunt date de ecuații
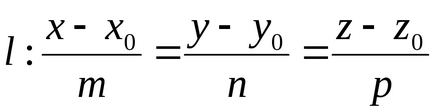
1) linia l se află în planul α, dacă
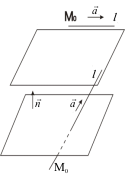
2) linia l este paralelă cu planul α, dacă