Produsul vector al vectorului de rază și vectorul de forță se numesc vectorul momentului forței relativ la pol.
Direcția vectorului momentului de forță poate fi găsită prin regula șurubului drept (Figura 10). Să transferăm vectorul
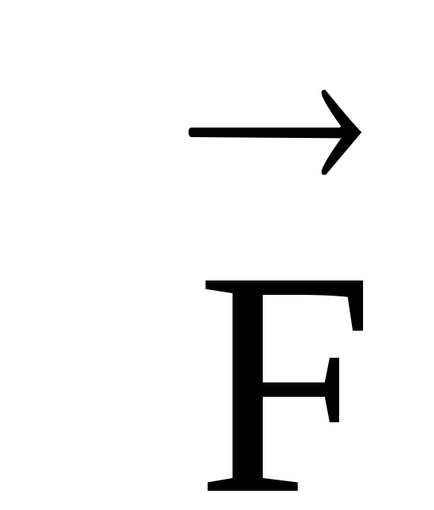
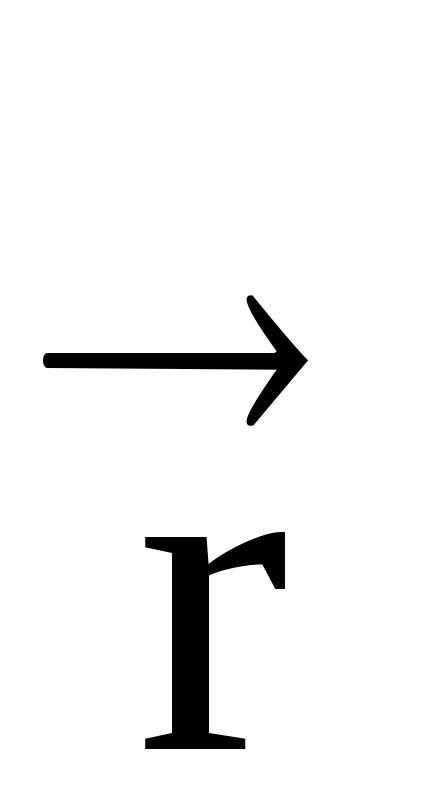
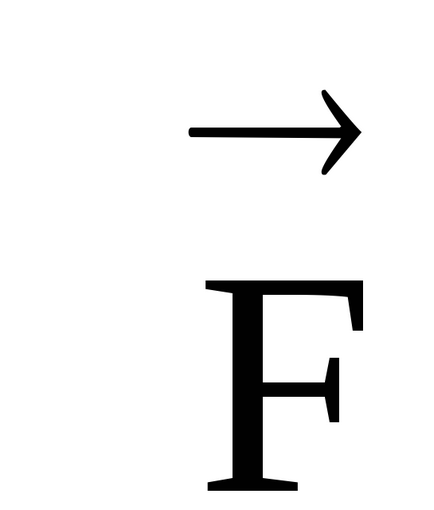
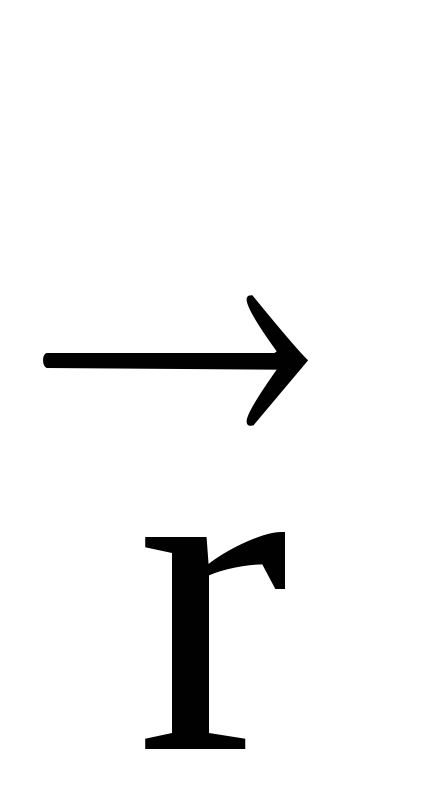
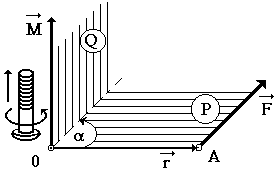
Notă. În cazul unui vector vector, vectori
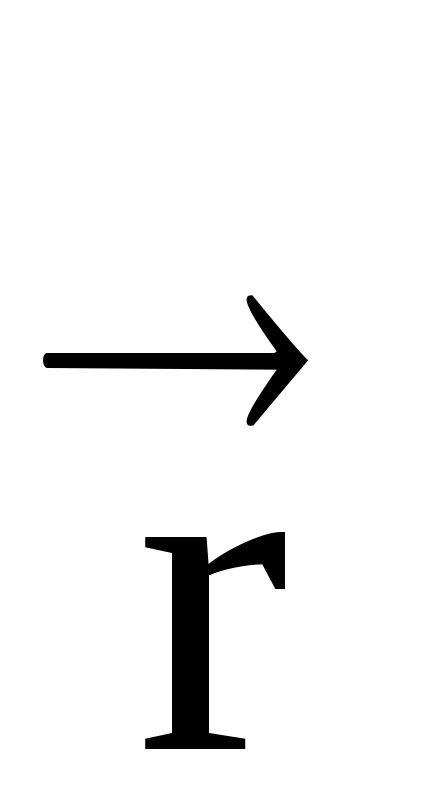
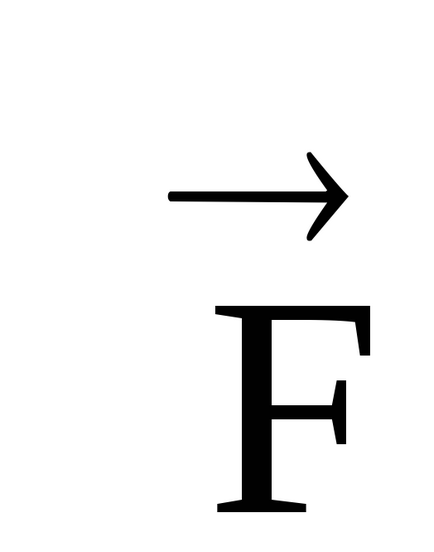
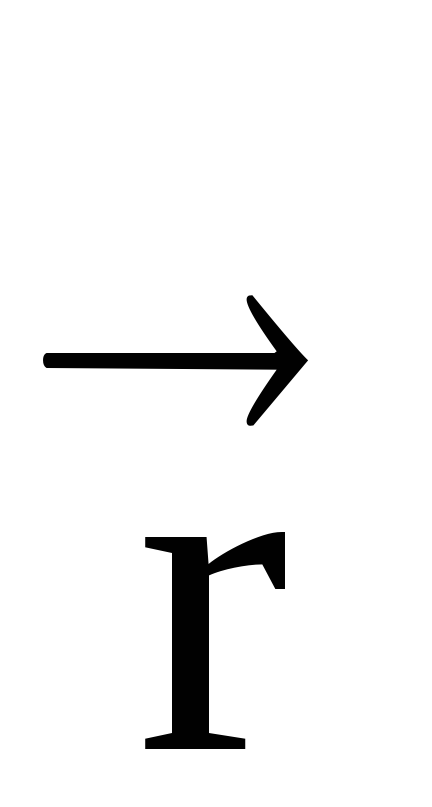
unde
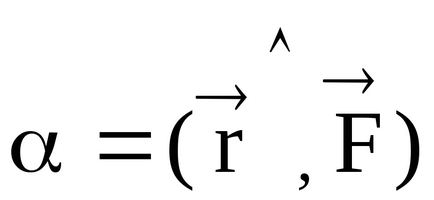
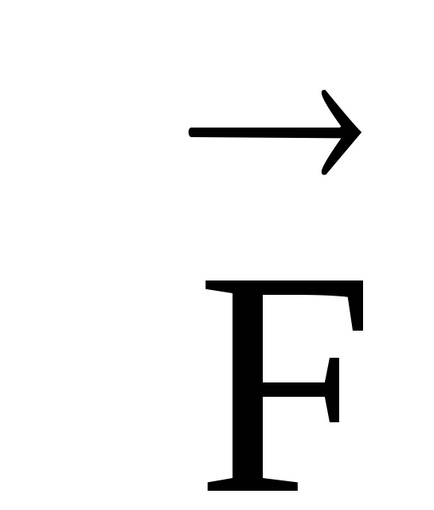
distanță
Se descompune forța care acționează pe o curbă metrică în două componente:
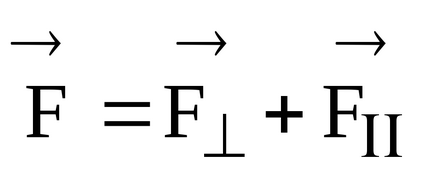
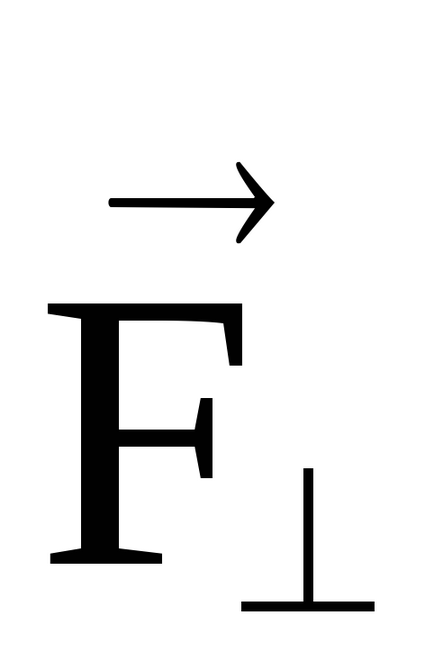
Conform Fig. 11 Cuplul determină numai forța
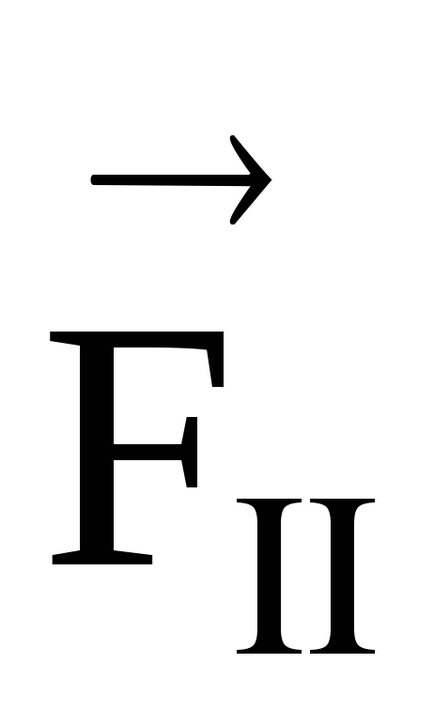
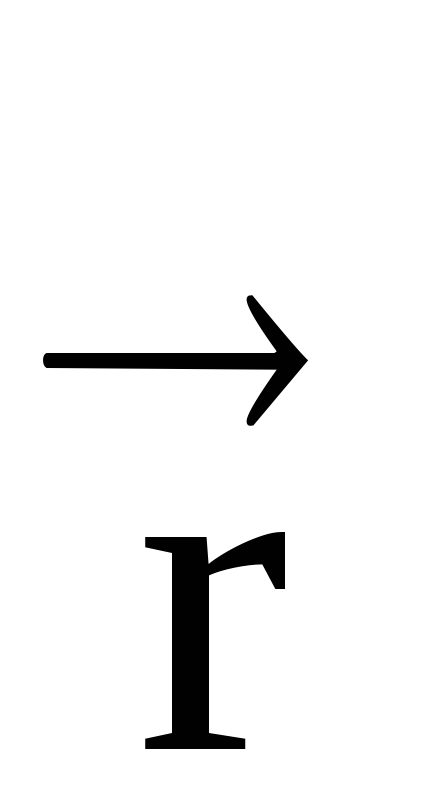
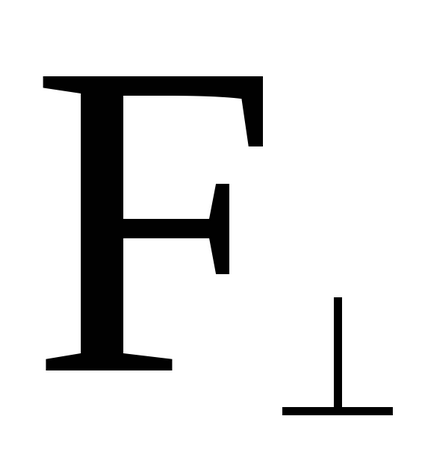
Forța vectorului momentului
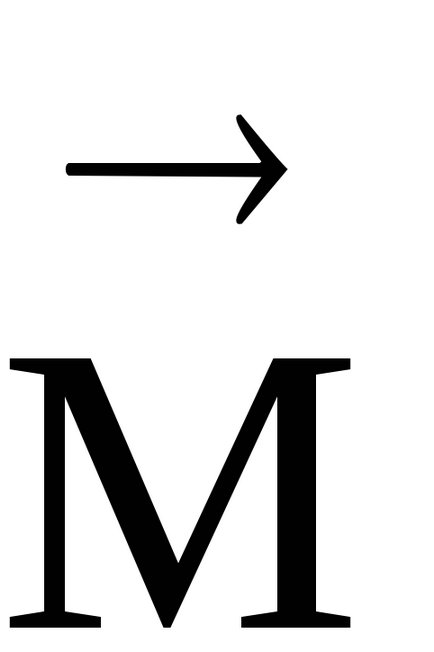
În SI, momentul forței este măsurat în Newtons înmulțit cu un metru (Nm).
2.13. Momentul rezultat al mai multor forțe
Dacă mai multe forțe acționează simultan asupra MT (corpul), forța rezultantă
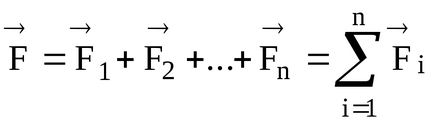
Vectorul momentului forței rezultante față de polul 0 este egal cu suma geometrică a vectorilor de moment ai forțelor componente față de același pol.
2.14. Momentul unei perechi de forțe
O pereche de forțe sunt două forțe egale în magnitudine, dar opuse în direcție, care nu se află pe aceeași linie dreaptă.
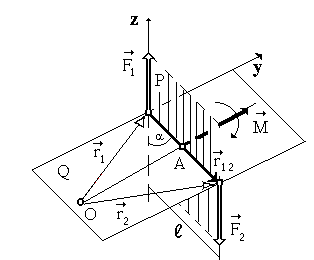
Din definiția perechii de forțe rezultă acest lucru
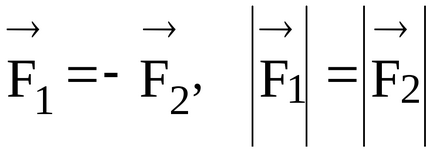
În Fig. 12 perechi de forțe de forță
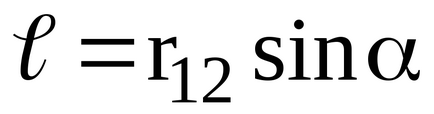
.
Momentul rezultat al forțelor
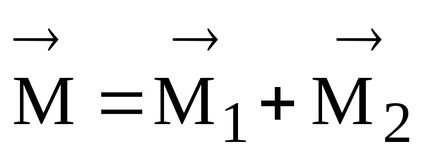
Apoi, momentul perechii de forțe relativ la polul 0 este scris în formular
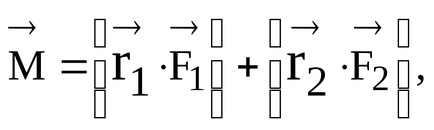
Având în vedere acest lucru
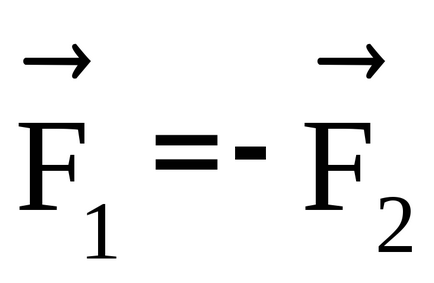
Vectorul de moment unghiular al perechii de forțe nu depinde de poziția polului 0.
2.15. Momentul forțelor interne
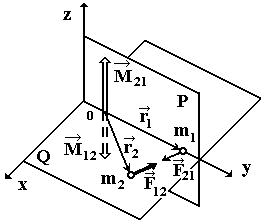
Un exemplu de forțe interne sunt forțele interacțiunii gravitaționale a două sau mai multe particule (corpuri) sau forța interacțiunii Coulomb a corpurilor (particulelor) încărcate ale unui sistem închis.
În baza celei de-a treia legi a lui Newton, aceste forțe sunt pereche de dimensiuni egale și în sens invers și se află pe aceeași linie de acțiune (Figura 13).
Într-adevăr, din moment ce
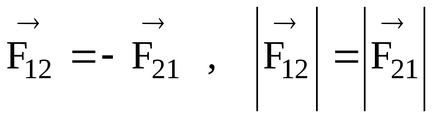
Momentele forțelor interne relative la același pol (puncte) 0 sunt egale în magnitudine și opuse în direcția:
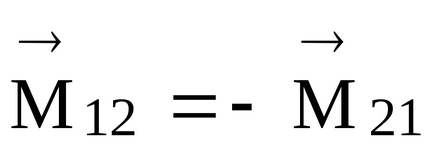
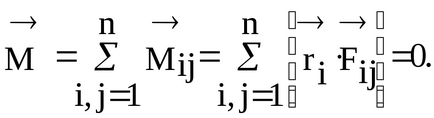
Notă. În cazul puterii centrale, când direcțiile de vectorii forțelor care acționează asupra m. M. Of sistemul trece printr-un pol fix 0, momentul forței este întotdeauna zero (deoarece umărul este absent).