Momentul unghiular al sistemului în raport cu punctul fix
În cazul în care corpul este rotit în jurul uneia dintre axele principale de inerție, direcția vectorului momentului cinetic al impulsului de corp coincide cu direcția vitezei sale unghiulare, și puls de cuplu poate fi exprimat în termeni de momentul de inerție
Momentul forței F în raport cu punctul fix O este cantitatea vectorului M. egală cu produsul vector al vectorului de rază r. trase de la punctul O la punctul A al aplicării forței, prin vectorul de forță F (regula pârghiei)
Forțați modulul momentului
unde l este lungimea perpendicularului scăzut de la punctul O la linia de acțiune a forței.
Momentul principal al forței (momentul rezultat) al mai multor forțe față de punctul fix O (pol) este vectorul M. egală cu suma geometrică a momentelor în raport cu punctul O al tuturor forțelor active
Momentul forței F în raport cu nemișcarea se numește magnitudinea. egală cu proiecția pe această axă a vectorului M al momentului forței F în raport cu un punct arbitrar O pe axa a
Dacă linia de acțiune a forței traversează axa sau este paralelă cu ea, atunci momentul de forță relativ la această axă este zero.
Prima derivată a timpului vremenitot sistemului impulsaLmehanicheskoy în raport cu orice punct fix O ravnaglavnomu Mvneshnotnositelno același timp punctul O al forțelor exterioare aplicate sistemului (legea de bază a dinamicii unui corp rigid care se rotesc în jurul unui punct fix)
Momentul unghiular al unui sistem închis cu privire la orice punct fix nu se modifică în timp (legea conservării momentului unghiular)
giroscoapele sunt corpuri masive omogene care se rotesc la o viteză unghiulară ridicată în jurul axei lor de simetrie, care este o axă liberă.
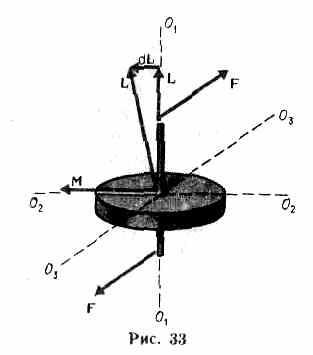
Dacă momentul forțelor externe aplicate giroscopului rotativ față de centrul său de masă este diferit de zero, atunci se observă un fenomen numit efect giroscopic. Se compune din faptul că, sub acțiunea unei perechi de forțe F aplicate pe axa giroscopului rotativ, axa giroscopului se rotește în jurul liniei drepte O3O3. și nu în jurul liniei drepte O2O2. așa cum ar părea natural la prima vedere (O1 O1 și O2 O2 se află în planul desenului, iar O3 O3 și forțele F sunt perpendiculare pe acesta).
9. Rotirea unui corp rigid în jurul unei axe fixe. Legea fundamentală a dinamicii mișcării de rotație a unui corp absolut rigid. Moment de inerție.
mișcare corp rigid, în care toate punctele liniei AB, legat rigid cu corpul rămâne nemișcat, numita rotație a corpului în jurul unei axe AB fix.
Acest corp rigid are un grad de libertate și poziția sa în spațiu este complet determinată de unghiul de rotație în jurul axei de rotație a unui convențional selectat, poziția inițială a corpului. O măsură a deplasării unui corp pentru un interval de timp mic dt este vectorul rotației elementare a corpului. Modulo este egal cu unghiul de rotație a corpului în timpul timpul dt, iar direcția coincide cu direcția de regulă transmite dreapta mișcare, direcția de rotație a mânerului coincide cu direcția de rotație a corpului (Fig. 1). Vectorul vitezei unghiulare
Izz este momentul de inerție în raport cu axa fixă.
Legea fundamentală a dinamicii unui corp rigid care se rotește în jurul unei axe fixe OZ
unde este accelerația unghiulară a corpului.
Momentul inerției sistemului mecanic față de axa fixă este cantitatea fizică Ja egală cu suma produselor de masă a tuturor punctelor materiale ale sistemului pe patrate ale distanțelor lor față de axa
10. Calcularea momentului de inerție a corpurilor de formă simplă. Teorema lui Steiner.
Momentul de inerție telaJotnositelno axă arbitrară egală cu suma momentului de inerție Jc a corpului în jurul unei axe care trece prin centrul de masă al corpului paralelă cu axa considerată, iar produsul de masa m pătratului corp de distanța d dintre axele (Teorema Huygens-Steiner)
Momente de inerție a corpurilor de formă simplă