Lăsați o funcție a unei variabile reale să fie dată. Este necesar să găsim rădăcinile ecuației
Problema găsirii rădăcinilor ecuației (1) este de obicei rezolvată în două etape. În prima etapă, rădăcinile sunt separate, adică selecția segmentelor care conțin doar o rădăcină. În a doua etapă, folosind aproximarea inițială, se construiește un proces iterativ, ceea ce face posibilă clarificarea semnificației rădăcinii care trebuie căutată.
Declarația metodei
Metoda secant este obținută prin metoda tangentelor prin înlocuirea aproximării diferenței:
Ca rezultat, obținem formula pentru procesul iterativ:
Metoda secantului este în două etape. adică noua aproximare "/> este determinată de cele două iterații anterioare și". /> În metoda (1) este necesar să se precizeze două aproximări inițiale și
Rata de convergență a metodei va fi liniară. -x * | = O (k ^ k-x *). "/>
Interpretare geometrică
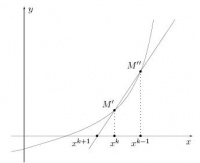
Observăm că ecuația secantului care trece prin punctele u va arăta astfel:
. Punerea și „/> Pot obține o formula (2) Aceasta înseamnă că“ /> - un punct de intersecție al abscisei cu axa noastră intersectând OX. Cu alte cuvinte, în intervalul, x ^ k] „> Funcția / este interpolate de un polinom de gradul întâi și următoarea apropiere“ /> rădăcină luate de acest polinom.
Un exemplu numeric
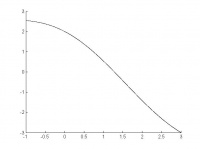
Luați în considerare funcția Utilizând metoda (2), găsim rădăcina ecuației. Codul sursă al programului care caută rădăcina ecuației prin metoda secant este prezentat în secțiunea "Fișiere".
Să luăm precizia ca aproximație inițială. "/> Ca rezultat, pentru 8 iterații primim rădăcina
Recomandări pentru programator
Opriți criteriile
De obicei, se ia unul dintre următoarele criterii de oprire:
Erori de rotunjire
În metoda secant, ca și în alte metode iterative de rezolvare a ecuațiilor, eroarea de rotunjire nu se acumulează. Eroarea totală de rotunjire este egală cu eroarea care a avut loc în ultima iterație și nu depinde de operațiile aritmetice efectuate în iterațiile anterioare.